 |
Выразим эту силу через характеристики поля. Поскольку
|
|
|
|
F = eE (5)
мы можем воспользоваться равенством выражений (4) и (5), т.е.
ma = eE
. (6)
Подставим (6) в (3), получаем, что
.
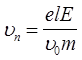При вылете частицы из конденсатора и попадания ее в сферу действия магнитного поля, на нее действует сила Лоренца, обусловленная составляющей un, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. В этой плоскости сила Лоренца является центростремительной силой, сообщающей перпендикулярное к скорости ускорение:
По второму закону Ньютона сила Лоренца может быть найдена как
(8)
Как мы знаем, что выражение для силы Лоренца имеет вид
FЛ = qunB. (9)
Приравняем выражения (8) и (9), получаем:
Отсюда
. (10)
Подставим (7) в (10), получаем
Шаг линии h можно найти, умножив ut на период обращения Т, определяемый формулой
т.е.
(11)
Из геометрических соображений, возникающих при анализе DАВС, мы находим то, что
Т.к. частица в конденсаторе движется по оси Ох равномерно со скоростью u0, а впоследствии составляющая ut = u0, т.е. в выражение (II) вместо ut подставим u0, и вместо un выражение (7), получаем
Вычисления:
Ответ: радиус винтовой траектории R =5 мм, шаг винтовой траектории h =3,6 см.
Тема 10
Электромагнетизм
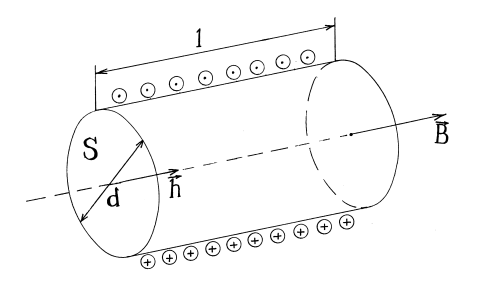
Задача 91
На соленоид длиной l =144 см и диаметром D =5 см надет проволочный виток. Обмотка соленоида имеет N =2000 витков, и по ней течет ток I= 1 А. Соленоид имеет железный сердечник. Какая средняя э.д.с. индуцируется в надетом на соленоид витке, когда ток в соленоиде выключается в течение времени t=2 мс?
| Дано: l =144 см D =5 см N =2000 t =2·10-3c I =2 A m0 = 12,56·10-7 Гн/м | Решение: Ниже дан график зависимости индукции В от напряженности магнитного поля для некоторого сорта железа. Средняя э.д.с. индукции в надетом на соленоид витке определяется формулой: |
| Еср -? | 
|
По условию задачи ток в соленоиде отключается, значит DФ2=0, т.е. магнитное поле соленоида временно прекратит существование, значит
|
|
|
(1)
Магнитный поток сквозь контур равен
Ф =BS cos j. (2)
Так как j =0, то cos j =1.
Зная диаметр поперечного сечения соленоида найдем его площадь, а именно
С учетом этого выражение (1) приобретает вид
(3)
Магнитная индукция В связана с напряженностью Н магнитного поля соотношением
В = mm0Н, (4)
где мы видим зависимость B=f(H), которую можно найти на графике, а напряженность внутри соленоида
(5)
Вычисляя числовое значение
находим соответствующую точку на оси В для данного числового значения, т.е. получаем числовое значение для магнитной индукции В, которая равна В =1,6 Тл.
Вычисления:
Ответ: средняя э.д.с. индукции в надетом на соленоид витке, когда ток выключается за данное время Еср =1,57 В.
Задача 92
В однородном магнитном поле, индукция которого В =0,1 Тл, вращается катушка, состоящая из N =200 витков. Ось вращения катушки перпендикулярна и ее оси и к направлению магнитного поля. Период обращения катушки Т =0,2 с, площадь поперечного сечения S =4 см2. Найти максимальную э.д.с. индукции Еmax во вращающейся катушке.
| Дано: В =0,1 Тл N =200 S = 10-4 м2 t =0,2c | Решение: Рассмотрим один виток соленоида. Магнитный поток, пронизывающий этот виток, изменяется по гармоническому закону Ф = BS cos j |
| Еmax -? | Как мы знаем, э.д.с. индукции в витке |
Угол j меняется со временем как j = wt,
где w - циклическая частота, равная
Отсюда
где Eo=BSw - максимальное значение э.д.с. индукции в витке.
Так как катушка представляет собой совокупность витков, то
Emax = NE0
или
Вычисления:
Ответ: максимальная э.д.с. индукции во вращающейся катушке равна 
.
Задача 93
Обмотка соленоида состоит из N витков медной проволоки, поперечное сечение которой S =l мм2. Длина соленоида l =25 см, его сопротивление R =0,2 0м. Найти индуктивность L соленоида.
|
|
|
| Дано: S = 10-6 м2 l = 0,25 м R =0,2 0м r = 17·10-9 Ом·м | Решение:
Сопротивление проводника, из которого было свито N витков, надетых на каркас соленоида, равно 
|
| Еср -? | где l¢ - длина проволоки, намотанной на весь соленоид. |
Отсюда
Участок этой проволоки, приходящейся на один виток, равен
т.е. величина 
является длиной окружности витка, вычисляемой по формуле
(1)
где r - радиус витка.
Отсюда
(2)
Подставляя (1) в (2), получаем:
(3)
площадь поперечного сечения соленоида равна
S = pr2 (4)
Подставим (3) в (4), получаем:
(5)
Величина индуктивности соленоида определяется формулой
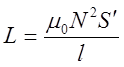(6)
Подставим (5) в (6), получаем
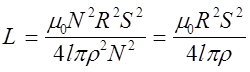
Вычисления:
Ответ: индуктивность соленоида равна 
.
Задача 94
Катушка с железным сердечником имеет площадь поперечного сечения S =20 cм2 и число витков N =500. Индуктивность катушки с сердечником L =0,28 Гн при токе через обмотку I =5 А. Найти магнитную проницаемость m железного сердечника.
| Дано: S = 2·10-3 м2 l = 0,28 Гн I =5 А m0 = 12,6·10-3 Гн/м | Решение:
Напряженность магнитного поля внутри соленоида
 (1)
|
| m -? | Индуктивность соленоида определяется |
формулой
(2)
Магнитная индукция В связана с напряженностью Н магнитного поля соотношением
В = mm0Н 
(3)
Подставим (3) в (2), получаем
Подставим (1) в (4), получаем
Отсюда
Найдем числовое значение магнитной индукции и впоследствии находим эту точку на оси координат графика B=f(H) и, приводя из этой точки параллельную линию оси ОН, найдем соответствующую ей точку на оси Н напряженности магнитного поля. После этой серии операций мы находим числовое значение Н. После этого все получившиеся числовые данные мы подставляем в формулу (3), откуда находим магнитную проницаемость железного сердечника
Вычисления:
По графику зависимости B=f(H), находим что Н =800 А/м.
Отсюда
Ответ: магнитная проницаемость железного сердечника соленоида равна m = 1800.
Задача 95
Сколько витков имеет катушка, индуктивность которой L =l мГн, если при токе I =1 А магнитный поток через катушку Ф =2 мкВб?
| Дано: L =l·10-3 Гн I =1 А Ф =2·10-6 Вб | Решение: Рассмотрим один виток данной катушки. Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный |
| N -? | поток Ф через контур из этого проводника про- |
порционален модулю индукции В магнитного поля внутри витка, а индукция магнитного поля в свою очередь пропорциональна силе тока в проводнике. Следовательно, магнитный поток через виток прямо пропорционален силе тока в контуре.
|
|
|
Полный магнитный поток Y через контур
Y = LI (1)
Поток через каждый из витков равен
Ф = BS,
а полный магнитный поток, сцепленный с соленоидом:
Y = NФ (2)
Сопоставляя (1)и (2), получаем
LI = NФ 
Вычисления:
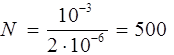(витков)
Ответ: катушка имеет 500 витков.
Задача 96
В магнитном поле, индукция которого В =0,1 Тл, помещена квадратная рамка из медной проволоки. Площадь поперечного сечения провода s = l мм2, площадь рамки S = 25 см2. Нормаль к плоскости рамки параллельна магнитному полю. Какое количество электричества q пройдет по контуру рамки при исчезновении магнитного поля?
| Дано: В =0,1 Тл S = 25·10-4 м2 s = 10-6 м2 r = 17·10-9 Ом·м | Решение:
Количество электричества, индуцируемого в рамке:
|
| q -? | где |
Ф1 - магнитный поток через рамку в первом состоянии
Ф2 - магнитный поток через рамку во втором состоянии.
По условию
Ф2 =0.
Сопротивление всей проволоки, входящей в контур
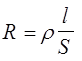(1)
где l - длина проволоки.
Мы знаем, что площадь контура
S = a2
где a - сторона квадрата, равная 
.
Отсюда
(2)
Подставим (2) в (1), получаем
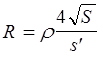
Так как
Ф1 = BS
то
Вычисления:
Ответ: количество электричества, которое пройдет по контуру рамки при исчезновении магнитного поля, равно q =74·10-3 Кл.
Задача 97
Круговой контур радиусом r =2 см помещен в однородное магнитное поле, индукция которого В =0,2 Тл. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R =l 0м. Какое количество электричества q пройдет через катушку при повороте ее на угол 90 градусов?
| Дано: В =0,2 Тл R =l 0м r =0,02 м a = 90° a = 180° | Решение:
Количество электричества, индуцируемого в рамке:
где Ф1 - магнитный поток через рамку в первом
|
| q -? | положении |
Ф1 = BS cos j
j - угол между нормалью к плоскости контура и направлением магнитного поля,
j = 0,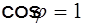 
Ф2 - магнитный поток через рамку в первом положении,
|
|
|
Ф2 = 0, т.к.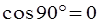 
Сопротивление контура с током
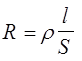
где l - длина окружности контура, равна l =2 pr. Площадь круга определяется формулой
S = pr2
В итоге получаем
Вычисления:
Ответ: количество электричества, которое пройдет через катушку при ее повороте на угол a = 90°, равно 
.
Задача 98
Электрическая лампочка, сопротивление которой в горячем состоянии R =10 Ом, подключается через дроссель к двенадцативольтовому аккумулятору. Индуктивность дросселя L =2 Гн, сопротивление r =1 Oм. Через какое время t после включения лампочка загорится, если она начинает заметно светиться при напряжении на ней U =6 В
| Дано: R =10 Ом r =1 Ом U0 =12 В L =2 Гн U =6 В | Решение:
Вследствие явления самоиндукции при включении э.д.с. ток нарастает по закону
|
| t -? | где R ' - сопротивление цепи. |
Умножим обе части выражения на R ', получаем:
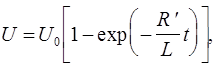
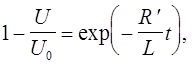
Прологарифмировав данное выражение, получаем:
(1)
Так как дроссель и лампочка включены последовательно, то сопротивление цепи в этом случае будет
R¢ = R + r
Следовательно, выражение (1) примет вид
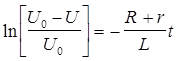
Вычисления:
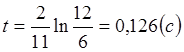
Ответ: через время, равное t =0,126 с после включения лампочки, она загорится.
Задача 99
Катушка имеет индуктивность L =0,144 Гн и сопротивление R =10 Ом. Через какое время t после включения в катушке потечет ток, равный половине установившегося?
| Дано: R =10 Ом L = 0,144 Гн I=I0/ 2 | Решение: Вследствие явления самоиндукции при включении э.д.с. ток протекает по закону: |
| t -? | 
|
где R - сопротивление цепи, в данном случае сопротивление катушки;
I0 - ток, установившийся в цепи после ее включения, в случае, когда t ® ¥.
Отсюда найдем время t, через которое выполнится условие I=I0 /2, значит
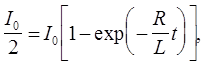
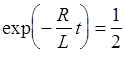
Прологарифмируем данное выражение, получаем:
Вычисления:
Ответ: через время t, равное t =0,01 с после включения в катушке потечет ток, равный половине установившегося.
Задача 100
Квадратная рамка из медной проволоки сечением S¢ =l мм помещена в магнитное поле, индукция которого меняется по закону 
где 
, 
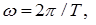
Площадь рамки S =25 см2. Плоскость рамки перпендикулярна к направлению магнитного поля. Найти зависимость от времени и наибольшее значение:
а) магнитного потока Ф, пронизывающего рамку,
б) э.д.с. индукции, возникающей в рамке,
в) тока I, текущего по рамке.
Дано:
| Решение: 1) Магнитный поток, пронизывающий рамку, равен Ф = BS cos a где a - угол между нормалью к плоскости и направлением магнитного поля. В данном случае a = wt Зная зависимость B=B(t), найдем зависимость Ф=Ф(t), так как S=const т.е. |
| Ф(t),E(t),I(t) -? |  (1)
|
Зная, что 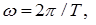преобразуем выражение (1):
(2)
Значения синуса в зависимости от угла меняется от -1 до 1, следовательно, максимальный магнитный поток Фтах, пронизывающий рамку будет при условии, когда
|
|
|
2) Э.д.с. индукции, возникающая в рамке, может быть найдена из данной формулы
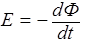(3)
Подставим выражение (1) в (3), получаем:
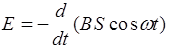
E=-BS( cos wt)=-BSw cos wt 
так как
, то 
3) Ток, текущий по рамке, можно найти из выражения
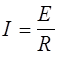(4)
Зная зависимость E=E(t), можно найти зависимость I=I(t), т.к. R=const. Сопротивление рамки определяется формулой
(5)
где l - длина проводника, из которого сделана рамка.
Зная площадь рамки S, мы найдем длины стороны рамки, т.к. рамка имеет форму квадрата, то ее площадь определяется формулой
S = a2 Þ
т.к. квадрат имеет четыре стороны, то
(6)
Подставим (6) в (5), получаем
(7)
Подставим (7) и (3)в (4), получаем
Так как
, то 
Вычисления:
Ответ: зависимость от времени t и наибольшее значение:
а) магнитного потока Ф, пронизывающего рамку,
б) э.д.с. индукции Е, возникающей в рамке,
в) тока I, текущего по рамке представлены в перечисленном порядке:
а) 
б) 
в) 
Литература
1. ФЭС.- М.: Советская литература, 1983
2. Сахаров Д.И., Косминков И.С. Сборник задач по физике. М: Учпедгиз, 1947
3. Боровой А.А., Финкельштейн Э.Б., Херувимов А.Н. Законы электромагнетизма. М: Наука, 1970
4. Новодворская Е.М. Методика проведения упражнений по физике во втузе. Изд. 2-е, доп. Учебн. пособие. М: Высшая школа, 1970
5. Зубов В.Г., Шальнов В.П. Задачи по физике. М: Физматгиз, 1963
6. Капица П.Л. Физические задачи. М: Знание, 1966
7. Баканина Л.П., Белонучкин В.Е. и др. Сборник задач по физике. М: Наука, 1971
8. Балаш В.А. Сборник задач по курсу общей физики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. М: Просвещение, 1978
9. Холидей Д., Резник Р. Вопросы и задачи по физике. Пособие для студентов пед. ин-тов. Пер. с англ. С.Н. Немирова. М: Просвещение, 1969
10. Сборник задач по общему курсу физики. Электричество и магнетизм. Под ред. И.А. Яковлева. – М: Наука, 1977
11. Гольдфарб Н.И. Сборник вопросов и задач по физике: Учеб. Пособие. – 5-е изд. – М: Высш. школа, 1982
12. Соколов А.А. Задачи по физике. М: Изд-во МХТИ, 1966
13. Зильберман А.Р., Сурков Е.Л. Задачи для физиков. М: Знание, 1971
14. Малов Н.Н. Задачи по физике с применением закона сохранения энергии. М: Просвещение, 1968
15. Понимаете ли вы физику? М: Знание, 1968
|
|
|
