 |
Использование приближенных способов измерения.
|
|
|
|
Есть точки, находящиеся на главных цепочках (опорных ходах) топосъемки (магистральные точки), а есть точки обрисовки (расстояния до стенок, до углов зала, короткие цепочки в тупики). Если мы ошибемся в определении координат точки обрисовки, то на качестве дальнейших измерений это не отразится. Если же мы ошиблись в координатах магистральной точки, то ошибка перейдет во все без исключения точки, отмеренные от нее.
Запомните! Ошибки измерений на магистралях накапливаются, а в точках обрисовки нет. Магистральные точки измеряются точными методами, а точки обрисовки могут измеряться приближенными способами.
Какие существуют приближенные способы измерений?
Во-первых, геометрические способы определения высоты потолка.
Во-вторых, все измерения на глаз. Например, при недоступности стенок в колодце.
В-третьих, антропометрия. То есть, измерение малых расстояний различными частями тела. Очень удобно при обрисовке стенок в узких ходах и меандрах. Занимает пару секунд.
Ширина раскинутых рук до кончиков пальцев в точности равно росту человека. Это заметил еще Леонардо да Винчи. Допустим, у меня рост 187см. Ширина размаха рук 188см. Мысленно добавив с каждой стороны длину мизинца (6см) получу в точности два метра. Теперь согну одну руку в локте, а другую оставлю вытянутой в сторону. Получу в точности 140см. Согну обе руки в локтях - 98см. Длина от кончиков пальцев до согнутого локтя - 51см. (старая русская мера длины - локоть как раз составляла 51 см.). Поднятая вверх рука достигает высоты 2м37см. Если еще и встать на цыпочки - то 2м45см. Расстояние между растопыренными большим пальцем и мизинцем - 27см. Померьте свои расстояния и выучите их наизусть. Это не трудно, а пользы будет много.
|
|
|
С какой точностью надо обрисовывать стенки?
Обрисовывать их с точностью в 10 см. совершенно бессмысленно. Допустим, боковая стенка имеет наклон. В зависимости от того, на какой высоте мы будем делать измерения, ширина может меняться от, скажем, 1 м. до, допустим, 3 м. А если есть подпотолочная щель, которая просматривается метров на пять? На мой взгляд, рельеф нужно прорисовывать так, чтобы он был узнаваем, то есть по наиболее характерным деталям, даже если они расположены на разных высотах.
Обработка данных топосъемки, погрешности, невязки.
В принципе имея полученные результаты, не представляет сложности построить сначала разрез-развертку, а затем план. Обозначаем начальный пикет для разреза, отмеряем транспортиром угол наклона и откладываем расстояние. Затем используя данные азимута, и проекцию расстояния с разреза последовательно строим план. Но данный метод в дополнение к ошибкам съемки добавляет ошибки построения. Для более точного построения можно рекомендовать построение методом координат.
Построение методом координат.
Идея очень простая. У нас есть две точки (пикеты) и данные замеров между ними:
· расстояние между точками – L;
· азимут – (a);
· и угол наклона – (b).
Если мы примем первую точку за нулевую (x=0, y=0, z=0), а ось "Y" направим на магнитный север, то мы легко получим координаты второй точки. Для двумерного случая каменоломен:
X=Lsin(a)
Y=Lcos(a)
Далее измеряем те же величины между второй и третьей точками, а координаты третьей точки получаем прибавлением к координатам второй точки вновь вычисленных X и Y. Таким образом мы получаем цепочку точек с известными координатами. Отстроив их на миллиметровке, мы получим "ход", который описывает нашу пещеру. А если мы в каждой точке измеряли расстояние от пикета до правой и левой стенок, то мы легко обрисуем наш ход и получим изображение еще и ширины штреков.
|
|
|
Для трехмерного случая природных пещер все несколько иначе. Казалось бы, мы должны получить трехмерные координаты точек:
X=Lsin(a)cos(b)
Y=Lcos(a)cos(b)
Z=Lsin(b)
Для плана пещеры (проекция на плоскость X-Y) мы берем первые две величины: X и Y. Проекция L на горизонтальную плоскость называется проложением. А проекция L на вертикальную ось z - превышением.
Но теперь мы хотим построить разрез-развертку.
Запомните! Разрез-развертка не есть сечение пещеры вертикальной плоскостью. И это не есть проекция на какие-либо вертикальные плоскости. А это есть разрез пещеры вертикальной поверхностью, изгибающейся вместе с изгибами пещеры.
Пример хорошо и тщательно сделанного разреза-развертки [5] даны в приложении №3.
Поэтому, для развертки мы вычисляем две величины:
L'=Lcos(b)
Z =Lsin(b)
Как видим, здесь нет ни Х, ни Y, вместо них вычисляется некая L', поскольку горизонтальное направление поверхности сечения постоянно меняется.
Если пещера ветвится, то на плане это отражается ясно и понятно. Но на разрезе-развертке ситуация неоднозначна. Обычно две разветвившиеся развертки рисуют на одной плоскости. Одну из ветвей можно пустить вправо, другую влево, можно в одну сторону (если они вновь соединяются). Это уже вопрос удобства. Так же как в каменоломнях мы отмечали ширину штрека, так же и в природных пещерах. Плюс к этому, мы оцениваем расстояния вверх и вниз. Обычно пишут. Вверх: "5м" или, если собственно потолок скрыт за уступами, то пишут ">10м" и т.п. Величина "вниз" тоже не всегда равна нулю: если мы стоим в распоре над меандром. Дно тоже далеко не всегда видно.
Вычисления лучше всего компьютерными средствами.
А можно ли не вычислять координаты?
Можно. Если, к примеру, надо нарисовать отснятое прямо на месте, а это горная местность, то можно на миллиметровке откладывать транспортиром азимуты, а линейкой или циркулем - расстояния. Значения синусов выбиты на обратной стороне горного компаса. Если нет транспортира, то можно использовать компас, сориентировав лист миллиметровки по линии север-юг. Но результат будет гораздо менее точен, по сравнению с вычислением координат. Главная проблема в том, что при построении транспортиром ошибка накапливается от точки к точке, а при вычислении координат нет (исходим из того, что компьютер не ошибается и цифры мы набиваем без ошибок). Кроме того, результат сильно зависит от масштаба построения и от аккуратности чертежника. Например, мы строим изображение в масштабе 1:500. Если, откладывая расстояния циркулем мы ошибемся на полмиллиметра, то это будет сразу ошибка в 25см. на местности. Все это легко проверить: постройте один и тот же участок сперва транспортиром, а потом по координатам. Результаты могут отличаться довольно сильно.
|
|
|
Запомните! Транспортиром строятся только черновые наброски, но не окончательный вариант топосъемки. Даже в полевых условиях строить по координатам. Для этого надо иметь с собой калькулятор и таблицы синусов и косинусов. Хотя выбор построения остается за вами.
Погрешности, невязки
В принципе, при работе с топосъемочными программами вам эти тонкости знать необязательно, но для общего развития и для проверки правильности работы конкретной программы (их далеко не Эйнштейны+Линусы Торнвальдсы, два в одном, пишут) будет полезно.
Что такое невязка?
| Пусть у нас есть некоторая кольцеобразно замкнутая полость. Мы построили на ней замкнутую топонитку: 1-2-3-4-1. Очевидно, что если бы мы производили измерения с бесконечно большой точностью, то при построении на карте последняя точка 1 совпала бы с первой точкой 1. Но каждое измерение мы делали с некоторой погрешностью, поэтому при построении последняя точка не попадет точно в первую, | 
|
а ляжет где-то поблизости. Назовем ее 1'. Расстояние 1-1' называется линейной невязкой.
Для чего она нам нужна?
Чтобы оценить качество топосъемки. Интуитивно понятно, что чем меньше невязка, тем лучше топосъемка. И чем длиннее замкнутый контур, тем больше будет невязка. Поэтому сказать: "невязка равна 1м." - значит ничего не сказать. Надо указать, для какого контура. Например: "невязка 1м на 10м" или "1м на 200м". В первом случае качество чрезвычайно плохое, во втором превосходное. По невязке мы получаем именно оценку качества, но не можем узнать качество точно. Почему? Во-первых, две ошибки могут уничтожить одна другую. Невязка близка нулю, а топосъемка при этом не верна. Во-вторых, не все ошибки отражаются на невязке.
|
|
|
Запомните! На невязке отражаются случайные ошибки. Систематические ошибки на ней не отражаются.
Систематические ошибки, это когда одна и та же ошибка добавляется неизменно в каждое измерение. Например, лимб компаса сбит на 10 градусов. При построении мы можем получить невязку близкой нулю, но вся картинка будет смещена на 10 градусов и точки будут отстоять от своих истинных мест на значительное расстояние. При состыковке с соседними участками съемки могут возникнуть значительные проблемы. Точно так же, если рулетка села после стирки. Все расстояния пропорционально увеличатся. Невязка тоже увеличится, но считаться она будет уже на кажущееся большее расстояние.
При топосъемке неизбежно имеются погрешности, так что построенная нитка хода будет отличаться от реальности. Если вы проходите не кольцевой путь, то сделать с этим ничего нельзя: что намеряли, то и намеряли. Однако при прохождении с топосъемкой кольцевого пути появляется дополнительная возможность: построенная нитка хода должна вернуться в точку, с которой началась. Однако, если вы построите нитку хода любой реальной топосъемки, вы из-за погрешностей никогда не попадете точно в точку, с которой начали. Но должны попасть. Это можно использовать для уменьшения погрешности топосъемки. Строго это описывается теорией вероятностей как распределение средневзвешенного значения пары случайных величин с учетом их плотностей распределений, но по простому выглядит следующим образом. Рассмотрим двумерный случай
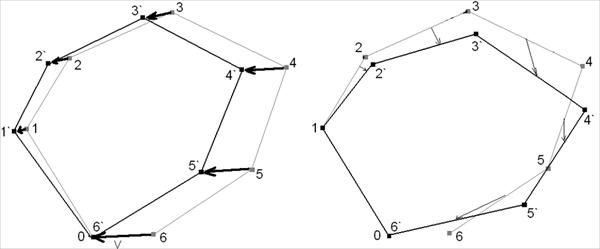
Способы разброса невязок кольца
Вы измерили несколько (N) пролетов, закольцевали топосъемку, построили нитку хода, но не пришли в исходную точку. Теперь можно применить следующую последовательность действий:
1) Находим недостающий до замыкания кольца вектор V (невязка кольца);
2) Если невязка слишком велика по сравнению с «габаритами» топосъемки — возможно где-то допущена ошибка (например, измерен обратный азимут вместо прямого), это нужно исправить;
3) Если невязка в пределах погрешностей измерений, то последнюю точку принудительно сдвигаем в первую, предпоследнюю — на (N-1)/N от вектора невязки в том же направлении, предыдущую к ней — на (N-2)/N и т.д.
Сразу видны недостатки этого способа. Длины пролетов измеряются намного точнее, чем углы, а при такой коррекции длины корректируются наравне с углами. Впрочем, при маленьких пролетах способ вполне адекватен из-за большего вклада погрешностей измерения длины и установки рулетки на точку.
|
|
|
Более адекватный способ для больших пролетов заключается в коррекции углов так, чтобы результирующая ломаная пришла в исходную точку. Однако, задача в этом случае становится гораздо более сложной, а решение неоднозначным.
Более совершенные способы основаны на рассмотрении т.н. «эллипса погрешностей» рассмотрен ниже.
Что делать, если в пещере нет ни одного замкнутого контура?
Типичная ситуация природных пещер: длина километров 5 и ни одного кольца. Догадливые уже поняли, что делать: на каком-нибудь участке пустить нитку съемки еще и в обратном направлении. Лучше всего взять участок метров в сто. Но есть существенная деталь: нельзя на обратном пути использовать те же пикеты. Здесь чистая психология. Пусть мы снимаем пятиметровками. А на обратном пути рулетка показала 4м97см. Есть соблазн записать показания как 5м00см. "Мы же помним, что тут было 5 метров ровно!" А этого делать нельзя.
Каковы нормативы качества съемки?
Условия природных пещер и горизонтальных каменоломен существенно отличаются. Поэтому и нормативы разные. Для природных пещер допустимой считается невязка 5-7м на 100м. Но при малых вертикальных углах можно достичь гораздо большей точности. На горизонтальных участках хорошим будет результат 1м. на 100м. В каменоломнях можно добиться и лучших результатов, скажем 0.5м/100м. Кто-то считает допустимыми невязки 5м/100м, кто-то разбрасывает даже невязки в 8-9м/100м. Все зависит от того, какой конечный продукт вы хотите получить. Лично я невязки в 3м/100м просто переснимаю, а не разбрасываю. Но это для хороших карт, в расчете на то, что их никому никогда не придется переделывать. Если карта делается для личного пользования, то каждый сам выбирает допустимые пределы, вплоть до съемки шагами без компаса.
Если получили невязку 0.00/100м?
Замечательно, но это вовсе не значит, что вы снимаете с бесконечно большой точностью. Пройдите этот же контур несколько раз. Получатся другие невязки. Скажем, 0.00м., 2.01м., 1.83м., 0.56м., 1.12м. Значит, средняя точность вашей съемки приблизительно 1.1м/100м, то есть отнюдь не бесконечная. А эти пять значений всего лишь случайные отклонения от среднего. Методически так и делается: берется несколько невязок и вычисляется среднее значение. Если в пещере нет или только один замкнутый контур, то в целях экономии времени считается только одна невязка.
Как разбрасывать невязки?
Действительно, если мы отстроили контур и последняя точка не совпала с первой, то надо что-то делать. Когда невязка в масштабе карты получилась 2-3 мм, то разброска делается вручную на глазок. Точки слегка смещаются со своих мест по линиям, параллельным линии 1-1'. Если же невязка больше, то применяются более точные и более правильные методически способы. Пусть у нас контур состоит из четырех точек 1-2-3-4-1'. Развернем контур в линию как показано на рисунке:
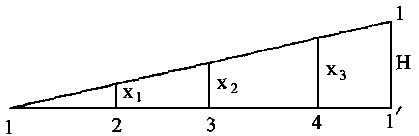
Перпендикулярно ему отложим невязку 1-1'. Теперь на топосъемке через все точки контура проведем серию линий, параллельных линии 1-1'. Циркулем будем брать расстояния поправок для каждой точки и откладывать их в одну и ту же сторону. По построенным точкам строим новый контур.
Сложности начинаются, когда к разбросанному контуру надо подстроить соседний контур, имеющий с первым общий штрек. Разбрасывать некоторые из точек повторно, нарушая разброску первого контура, или разбрасывать во втором контуре не все точки, а только часть? Точного решения здесь нет - это на усмотрение автора съемки.
|
|
|


