Внешний фотоэффект и его законы. Уравнение Энштейна. Внутренний фотоэффект

Внешним фотоэффектом называется явление испускания электронов веществом под действием электромагнитного излучения. Внутренним фотоэффектом называется явление появление свободных электронов в веществе (полупроводниках) под действием электромагнитного излучения Связанные (или валентные) электроны становятся свободными (в пределах вещества). В результате уменьшается сопротивление вещества.

Законы внешнего фотоэффекта:

1.При неизменном спектральном составе излучения сила тока насыщения (или число фотоэлектронов, испускаемых катодом за единицу времени) прямо пропорциональна падающему на фотокатод потоку излучения (интенсивности излучения).

2.Для данного фотокатода максимальная начальная скорость фотоэлектронов, а, следовательно, их максимальная кинетическая энергия определяется частотой излучения и не зависит от его интенсивности.

3.Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота излучения ν₀, при которой еще возможен внешний фотоэффект. Отметим, что значение ν₀ зависит от материала фотокатода и состояния его поверхности.

Объяснение внешнего фотоэффекта с точки зрения волновой теории света противоречило экспериментальным данным. Согласно волновой теории под действием поля электромагнитной волны в металле возникают вынужденные колебания электронов в атоме с амплитудой тем большей, чем больше амплитуда вектора напряженности электрического поля волны E_o (и, следовательно, интенсивность света I~E_o²). В результате этого электроны могут покидать металл и выходить из него, т.е. может наблюдаться внешний фотоэффект. Тем выше должна быть и скорость вылетевших электронов, т.е. кинетическая энергия фотоэлектронов должна зависеть от интенсивности излучения, что противоречит опытным данным. По этой теории излучение любой частоты, но достаточно большой интенсивности должно вырывать электроны из металла, т.е. красной границы фотоэффекта не должно быть.

А. Эйнштейн в 1905 г. показал, что явление фотоэффекта и его закономерности могут быть объяснены на основе квантовой теории М. Планка. Согласно Эйнштейну, свет (излучение) частотой ν не только испускается, как это предполагал М. Планк, но и распространяется в пространстве и поглощается веществом отдельными порциями (квантами), энергия которых

E_o = hν, (1)

где h = 6,626176*10^-34 Дж×с – постоянная Планка,

Позднее кванты излучения получили название фотонов. По Эйнштейну, каждый квант поглощается только одним электроном. Если энергия кванта больше чем работа выхода электрона из металла, т.е. hν>=А_вых, то электрон может покинуть поверхность металла. Остаток энергии кванта идет на создание кинетической энергии электрона, покинувшего вещество. Если электрон освобождается излучением не у самой поверхности, а на некоторой глубине, то часть полученной энергии может быть потеряна вследствие случайных столкновений электрона в веществе, и его кинетическая энергия окажется меньшей. Следовательно, энергия падающего на вещество кванта излучения расходуется на совершение электроном работы выхода и сообщение вылетевшему фотоэлектрону кинетической энергии.

Закон сохранения энергии для такого процесса будет выражаться равенством

(2)

Это уравнение называется уравнением Эйнштейна для внешнего фотоэффекта.

Из уравнения Эйнштейна непосредственно следует, что максимальная кинетическая энергия или скорость фотоэлектрона зависит от частоты излучения. С уменьшением частоты излучения кинетическая энергия уменьшается и при некоторой частоте может стать равной нулю. Уравнение Эйнштейна в этом случае будет иметь вид

h ν₀= А_вых.

Частота ν₀, соответствующая этому соотношению будет иметь минимальное значение и является красной границей фотоэффекта. Из последнего ясно, что красная граница фотоэффекта определяется работой выхода электрона и зависит от химической природы вещества и состояния его поверхности. Длина волны, соответствующая красной границе фотоэффекта, может быть рассчитана по формуле . При hν<А_вых фотоэффект прекращается. Число высвобождаемых вследствие фотоэффекта электронов должно быть пропорционально числу падающих на поверхность вещества квантов излучения, а, следовательно, потоку излучения Ф.

С изобретением лазеров были получены большие мощности излучения, в этом случае один электрон может поглотить два и более (N) фотонов (N=2…7). Такое явление называется многофотонным (нелинейным) фотоэффектом. Уравнение Эйнштейна для многофотонного фотоэффекта имеет вид

В этом случае красная граница фотоэффекта может смещаться в сторону более длинных волн.

Характер зависимости фототока I от разности потенциалов между анодом и катодом U (вольт – амперная характеристика или ВАХ) при постоянном потоке излучения на фотокатод монохроматического излучения приведен на Рис. 1.

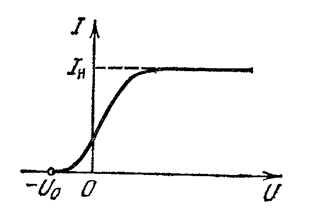
Рис. 1.

 

Существование фототока при напряжении U=0 объясняется тем, что фотоэлектроны, испускаемые катодом, имеют некоторую начальную скорость и, соответственно, кинетическую энергию, а, следовательно, могут достигать анода без внешнего электрического поля. По мере увеличения значения U (в случае положительного потенциала на аноде) фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Пологий характер этого участка вольтамперной характеристики свидетельствует о том, что электроны вылетают из катода с различными скоростями. Максимальное значение фототока, называемое током насыщения I_нас, достигается при таком значении U, при котором все электроны, испускаемые катодом, попадают на анод. Значение I_нас. определяется числом фотоэлектронов, испускаемых катодом за 1с и зависит от величины потока излучения, падающего на фотокатод.

Если анод имеет отрицательный потенциал, то образующееся электрическое поле тормозит движение фотоэлектронов. Это приводит к уменьшению числа электронов, достигающих анода, а, следовательно, и уменьшению фототока. Минимальное значение напряжения отрицательной полярности, при котором ни один из электронов, даже обладающий при вылете из катода максимальной скоростью, не может достигнуть анода, т.е. фототок становится равным нулю, называется задерживающим напряжением U_o.

Значение задерживающего напряжения связано с начальной максимальной кинетической энергией электронов соотношением

(3)

С учетом этого, что уравнение Эйнштейна можно записать в также в виде

hν=А_вых + eU₀.

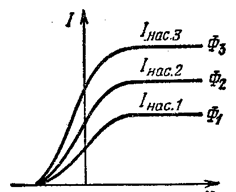
Если менять величину падающего на катод потока излучения при одном и том же спектральном составе, вольтамперные характеристики будут иметь вид, приведенный на Рис. 2.

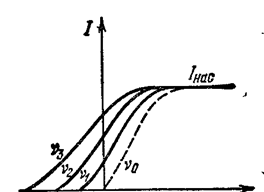
Если при неизменной величине потока излучения менять его спектральный состав, т.е. частоту излучения, то вольтамперные характеристики будут меняться, как показано на Рис.3.

 

 

U₀ 0 U U₀₃ U₀₂ U₀₁ 0 U

F₃>F₂>F₁ n=const n₃>n₂>n₁ F= const

Рис. 2. Рис. 3.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: