 |
Вопрос 12 Механические колебания
|
|
|
|
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.
гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса).
Гармонические колебания величины s описываются уравнением типа
| s = A cos (ω0 + φ), | (1.81) |
где А – максимальное значение колеблющейся величины, называемое амплитудой колебания, ω0 – круговая (циклическая) частота, (φ – начальная фаза колебания в момент времени t = 0, (ω0t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до - А.
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2π, т. е.
| ω0(t+T)+φ =(ω0t +φ)+2π | (1.82) |
откуда
| Т=2π/ω0. | (1.83) |
Величина, обратная периоду колебаний,
| ν = 1/T | (1.84) |
т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (1.83) и (1.84), получим
| ω0=2πν. | (1.85) |
Единица частоты – герц (Гц): 1 Гц – частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
| ds /dt = -Aω0 sin(ω0 t +φ) = Aω0 cos (ω0t +φ+π/2); | (1.86) | |
| d2s / dt2 = -Aω02 cos (ω0 t + φ)= Aω02cos (ω0 t+φ+π), | (1.87) | |
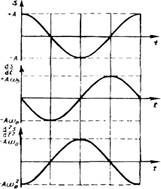 т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (1.86) и (1.87) соответственно равны Аω0 и Аω02. Фаза величины (1.86) отличается от фазы величины (1.81) на π/2, а фаза величины (1.87) отличается от фазы величины (1.81) на π. Следовательно, в моменты времени, когда s = 0, ds/dt приобретает наибольшие значения; когда же s достигает отрицательного максимального значения, то d2s /dt2 приобретает положительное наибольшее значение (рисунок 1.53).
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (1.86) и (1.87) соответственно равны Аω0 и Аω02. Фаза величины (1.86) отличается от фазы величины (1.81) на π/2, а фаза величины (1.87) отличается от фазы величины (1.81) на π. Следовательно, в моменты времени, когда s = 0, ds/dt приобретает наибольшие значения; когда же s достигает отрицательного максимального значения, то d2s /dt2 приобретает положительное наибольшее значение (рисунок 1.53).
|
|
|
Из выражения (1.87) следует дифференциальное уравнение гармонических колебаний
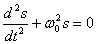
| (1.88) |
(где s=A cos (ω0t +φ)).
Решением этого уравнения является выражение (1.81).
Свободные гармонические колебания. Скорость, ускорение при гармонических колебаний. Кинетическая и потенциальная энергия. Закон сохранения энергии при гармонических колебаниях.
Существуют периодические и непериодические колебания. Особое место среди первых из них занимают гармонические колебания.
Гармоническими называются колебания, для которых изменяющаяся величина зависит от времени по закону синуса или косинуса.
Уравнение гармонических колебаний можно записать в виде:
x = A*sin(wt + f0), где
x - смещение точки от положения равновесия,
A - амплитуда колебаний,
(wt+f0) - фаза колебаний,
f0 - начальная фаза,
w - частота,
t - время.
Скорость гармонического колебания

Ускорение колеблющейся точки 
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:


Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Амплитуда и частота затухающих колебаний. Декремент, логарифмический декремент затухания, время релаксации, добротность.
Затухающие колебания -колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления.
1. Механические:
Пусть Fсопр=-hv (сила сопротивления пропорциональна скорости колебаний) = - hx¢, h -к-т сопротивления.
Тогда по 2-му з-ну Ньютона: mx¢¢=- hx¢ - кх(=Fтр).
|
|
|
Обозначим :b=h/2m -коэффициент затухания; w02=k/m- собственная частота свободных колебаний.
x¢¢+2bх¢+w02х=0
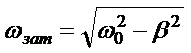 -собственная частота свободных незатухающих колебаний(-сколько раз за p секунд тело пройдет через положение равновесия)
-собственная частота свободных незатухающих колебаний(-сколько раз за p секунд тело пройдет через положение равновесия)
При условии b>w0 - затух колебаний нет - апериодический возврат в положение равновесия
При условии b<w0 - затухающие колебания
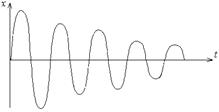 Решение уравнения - х(t)=а0е- btcos( wt+a) a-начальная фаза.
Решение уравнения - х(t)=а0е- btcos( wt+a) a-начальная фаза.
Логарифмический декремент и коэффициент затухания:
Если A(t), A(t+T), амплитуды двух последовательных колебаний то отношение 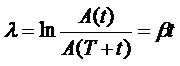 называется логарифмическим декрементом затухания
называется логарифмическим декрементом затухания

Физический и математический маятник.Физический маятник. Дифференциальное уравнение колебания и его решение. Период колебаний физического маятника. Приведенная длина. Математический маятник. Период колебания математического маятника.
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 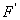 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения  и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
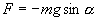
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 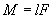 , и момент инерции:
, и момент инерции:
M = FL.
Момент инерции J в данном случае
Угловое ускорение:
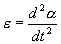
С учетом этих величин имеем:
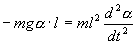
или
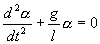
| (7.8) |
Его решение
 ,
,
где 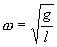 и и 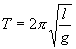
| (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
|
|
|
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
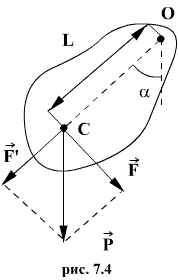
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
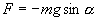
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
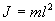 . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

| (7.10) |

| (7.11) |
Решение этого уравнения
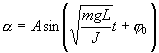
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 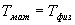 или
или
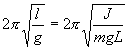 .
.
Из этого соотношения определяем
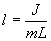
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Вопрос 16 Идеальный газ
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку.
При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
|
|
|
| m0v–(–m0v)=2m0v, | (2.21) |
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой v t (рисунок 2.5). Число этих молекул равно n Sv t (n – концентрация молекул).
Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 n Sv t. При столкновении с площадкой эти молекулы передадут ей импульс
| P = 2m0v1/6nSvt = 1/3nm0v2St | (2.22) |
Тогда давление газа, оказываемое им на стенку сосуда,
| P = P/(tS) = 1/3nm0v2. | (2.23) |
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2,..., vN, то целесообразно рассматривать среднюю квадратичную скорость
<vкв>= 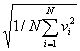 , ,
| (2.24) |
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
| p = 1/3nm0<vКВ>2. | (2.25) |
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов.
| PVm = RT |
Уравнению
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева.
В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах.
|
|
|


