Вопрос 42 Явление самоиндукции

Электрический ток, протекающий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара — Лапласа, пропорциональ­на току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:

Ф = LI

(4.35)

где коэффициент пропорциональности L называется индуктивностью контура.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с., это явление называется самоиндукцией

L=0 Соленоид

э. д. с. самоиндукции .

Если контур не деформируется и магнитная проницаемость среды не изменяется, то

L=const и s=-L

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Согласно правилу Ленца, экстратоки самоиндукции, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток.

I=I0e-t/

(4.39)

где =l/r— постоянная, называемая временем релаксации ( время, в течение которого сила тока уменьшается в е раз).

Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (кривая I на рис. 4.21). Чем больше индуктивность цепи и меньше ее сопротивление, тем больше  и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании. I=I₀(1-e^-t/)

Вопрос 43 Энергия магнитного поля тока

 

Рассмотрим контур индуктивностью L, по которому течет ток I. С кон­туром сцеплен магнитный поток (см. (4.35)) Ф=LI. При изменении тока на dl магнитный поток изменяется на dФ=LdI. Для изменения магнитного потока на величину dФ необходимо совершить работу dA=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф будет равна .

Следовательно, энергия магнитного поля, связанного с контуром,

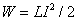
однородное магнитное поле внутри длинного соленоида.

.

 

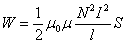
Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с объемной постоянной плотностью

 

 

Вопрос 44 Закон полного тока

Циркуляцией вектора В по заданному замкнутому контуру называется интеграл

где dl — вектор элементарной длины контура, направленной вдоль обхода контура, B_l=Bcos — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода),  — угол между векторами В и d l.

Закон полного тока для магнитного поля в вакууме: циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной ₀ на алгебраическую сумму токов, охватываемых этим контуром:

(4.9)

где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром.

Внутри соленоида поле является однородным, а снаружи — неоднородным и очень слабым.

Для магнитной индукции поля внутри соленоида (в вакууме):

B=0 NI / l

B=₀NI/(2r), где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и В2r=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).

Вопрос 45 Ферромагнетизм

Ферромагнетики — сильномагнитные вещества, обладающие спонтанной намагниченностью даже при отсутствии внешнего магнитного поля. Ферромагнитными свойствами обладают — железо, кобальт, никель, гадолиний, их сплавы и соединения.

Для ферромагнетиков зависимость J от Н является нелинейной. По мере увеличения намагничивающего поля возрастает степень ориентации молекулярных магнитных моментов по полю и намагниченность быстро растет. Процесс замедляется с уменьшением доли неориентированных моментов, когда все моменты будут ориентированы по полю, дальнейшее увеличение J прекращается и наступает магнитное насыщение.

Магнитная индукция B=₀(H+J) в слабых полях растет быстро с ростом Н вследствие увеличения J. Изменение магнитной индукции В в сильных полях происходит по линейному закону, поскольку J=J_нас. Особенностью ферромагнетиков являются большие значения  (например, для железа — 5000, для сплава супермаллоя — 800000!) и зависимость  от Н (рис. 4.34). Вначале  растет с увеличением Н, достигает максимума и начинает уменьшаться, приближаясь в случае сильных полей к 1 (=B/(₀H)=1+J/H, поэтому при J=J_нас=const с ростом Н отношение J/H0, a l).

Важнейшее практическое значение имеет зависимость магнитных свойств предыстории намагничения. Это явление получило название магнитного гистерезиса. Если намагнитить ферромагнетик до насыщения (точка 1, рис. 4.34), а затем начать уменьшать напряженность Н намагничивающего поля, то, как показывает опыт, умень­шение J описывается кривой 1—2, лежащей выше кривой 1—0. При H=0 J отличается от нуля, т. е. в ферромагнетике наблюдается остаточное намагничение J_oc. Остаточное намагничение используют в постоянных магнитах. Намагничение обращается в нуль под действием поля Н_C, имеющего направление, противоположное полю, вызвавшему намагничение. Напряженность Н_C называется коэрцитивной силой.

При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3—4), и при Н=-H_нас достигается насыщение (точка 4). Затем ферромагнетик можно опять размагнитить (кривая 4—5—6) и вновь перемагнитить до насыщения (кривая 6—1).

Таким образом, при действии на ферромагнетик переменного магнитного поля намагниченность J изменяется в соответствии с кривой 1—2—3—4—5—6—1, которая называется петлей гистерезиса (от греч. «запаздывание»). Гистерезис приводит к тому, что намагничение ферромагнетика не является однозначной функцией Н, т. е. одному и тому же значению Н соответствует несколько значений J.

Различные ферромагнетики дают разные гистерезисные петли. Ферромагнетики с малой (в пределах от нескольких тысячных до 1—2 А/см) коэрцитивной силой Н_C (с узкой петлей гистерезиса) называются мягкими, с большой (от нескольких десятков до нескольких тысяч ампер на сантиметр) коэрцитивной силой (с широкой петлей гистерезиса) — жесткими. Величины Н_C, J_oc и _max определяют применимость ферромагнетиков для тех или иных практических целей. Так, жесткие ферромагнетики (например, углеродистые и вольфрамовые стали) применяются для изготовления постоянных магнитов, а мягкие (например, мягкое железо, сплав железа с никелем) — для изготовления сердечников трансформаторов.

Ферромагнетики обладают еще одной существенной особенностью: для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик. Переход вещества из ферромагнитного состояния в парамагнитное, происходящий в точке Кюри, не со­провождается поглощением или выделением теплоты, т. е. в точке Кюри происходит фазовый переход II рода.

Наконец, процесс намагничения ферромагнетиков сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикции. Величина и знак эффекта зависят от напряженности Н намагничивающего поля, от природы ферромагнетика и ориентации кристаллографических осей по отношению к полю.

Природа ферромагнетизма

Качественная теория ферромагнетизма была разработана французским физиком П. Вейссом. Последовательная количественная теория на основе квантовой механики развита Я. И. Френкелем и немецким физиком В. Гейзенбергом.

Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличия внешнего намагничивающего поля. Вейсс предположил, что ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.

При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтанной намагниченности. Поэтому с ростом H намагниченность J (см. рис. 4.32) и магнитная индукции В (см. рис. 4.33) уже в довольно слабых полях растут очень быстро. Этим объясняется также увеличение  ферромагнетиков до максимального значения в слабых полях. Эксперименты показали, что зависимость В от Н не является такой плавной, а имеет ступенчатый вид, как показано на рис. 4.33. Это свидетельствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.

При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепловое движение не в состоянии быстро дезориентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис. 4.34). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную силу; размагничиванию способствуют также встряхивание и нагревание ферромагнетика. Точка Кюри оказывается той температурой, выше которой происходит разрушение доменной структуры.

Существование доменов в ферромагнетиках доказано экспериментально. Прямым экспериментальным методом их наблюдения является метод порошковых фигур. На тщательно отполированную поверхность ферромагнетика наносится водная суспензия мелкого ферромагнитного порошка (например, магнетита). Частицы оседают преимущественно в местах максимальной неоднородности магнитного поля, т. е. на границах между доменами. Поэтому осевший порошок очерчивает границы доменов и подобную картину можно сфотографировать под микроскопом. Линейные размеры доменов оказались равными 10^-4—10^-2 см.

 

Вопросы 46 Основы единой теории электромагнитного поля Максвелла

Ток смещения — это изменяющееся со временем электрическое поле, поэтому существует не только в вакууме или диэлектриках, но и внутри проводников, по которым проходит переменный ток.

Плотность полного тока по Максвеллу

.

Полный ток в цепях переменного тока всегда замкнут, т. е. в проводнике существует ток проводимости, а в диэлектрике (вакууме) - ток смещения, который замыкает ток проводимости.

В основе теории Максвелла лежат четыре уравнения:

1. Электрическое поле может быть как потенциальным (E _Q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е=Е _Q +Е _B. Так как циркуляция вектора E _Q равна нулю (см. (4.78)), а циркуляция вектора Е_B определяется выражением (4.77), то циркуляция вектора напряженности суммарного поля

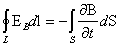
(4.83)

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (4.82)):

(4.84)

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами, либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (3.44)):

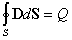
(4.85)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (4.83) запишется в виде

(4.86)

4. Теорема Гаусса для поля В (см. (4.29)):

(4.87)

Материальные уравнения. Фундаментальные уравнения Максвелла еще не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно.

Уравнения Максвелла необходимо дополнить материальными уравнениями, в которые входят величины, характеризующие индивидуальные свойства среды.

Материальные уравнения наиболее просты в случае достаточно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков, материальные уравнения имеют следующий вид:

D= ₀ E, B= ₀ H, j=  E+Е*, где ₀ и ₀ — соответственно электрическая и магнитная постоянные,  и  — соответственно диэлектрическая и магнитная проницаемости,  — удельная проводимость вещества, Е* — напряженность поля сторонних сил, обусловленная химическими или тепловыми процессами.

Уравнения Максвелла линейны. Они содержат только первые производные полей Е и В по времени и пространственным координатам и первые степени плотности электри­ческих зарядов ρ и токов j. Свойство линейности уравнений Максвелла непосредственно связано с принципом супер­позиции; если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.

Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистски инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически валентны друг другу

Для стационарных полей (Е= const и B=cоnst) уравнения Максвелла примут вид

; ; ; ,

 

 

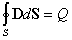⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: