Оценка динамики факторов роста предприятия.

Статистическая сводка является сложной операцией по научной обработке данных статистического наблюдения, при которой тысячи, а иногда и многие миллионы индивидуальных показаний превращаются в стройную систему статистических выкладок. Статистическая сводка ведется на основе всестороннего теоретического анализа изучаемых явлений и процессов. Если такой анализ не предшествует сводке, то возможен недостаточно полный охват сводкой изучаемого явления, выпячивание при этом частных вопросов и т.п. Предварительный теоретический анализ должен способствовать тому, чтобы во время сводки не терялись основные черты исследуемых явлений, чтобы статистические итоги отчетливо характеризовали эти черты. Группировка материала статистического наблюдения является одной из важнейших работ статистического исследования вообще. Несмотря на кажущуюся легкость проведения группировок и технический характер дела, эта операция является

В качестве группировочных труднейшим этапом статистической работы. Прежде чем проводить любую группировку, необходимо определить группировочный признак, или основание группировки. Основанием группировки является признак, по которому совокупность расчленяется на группы. Выбор основания группировки зависит от цели данной группировки и предварительного экономического анализа. Данные по наблюдению приведены в (приложение 2)признаков служат затраты на оплату труда на 1000 шт продукции и выпуск продукции в сутки. Для изучения интенсивности вариаций уровней этих признаков приведены в (приложении 3 и 4), где приводятся ранжированные ряды.

Вариация по затратам на заработную плату и по продуктивности незначительная. Строим интервальный ряд, с равными интервалами, при n=3, исходя из (см. приложениe 4).

Интервал в группах:

Данные сводим в (см. приложение 5) по затратам на заработную плату.

Большинство наблюдений – 5, которые при среднем уровне затрат на заработную плату в расчете на 1000 шт.продукции (13,50 руб.), имеют среднюю себестоимость в данной совокупности. Минимальное число наблюдений – 2, которые при самом высоком уровне затрат на заработную плату (17,15 руб.), имеют максимальную себестоимость – 509,72р. Связь между факторным и результативным признаками проявляется следующим образом: с увеличением затрат на заработную плату себестоимость тоже увеличивается, т.е. связь прямолинейная и прямая. По второму группировочному признаку – продуктивности вариация уровней также невелика. Группировку проводим как в случае с неравными интервалами. Данные сводим в групповую таблицу (см.приложение 6).

Минимальную выработку(265шт) имеют пять наблюдений, у них же и самая низкая себестоимость (132,38). Максимальную продуктивность видим у трех наблюдений (334шт), которые имеют себестоимость наиболее близкую к средней по совокупности (450,46р.). Из приведенной таблицы нельзя сказать, как проявляется связь между признаками. Для более глубокого изучения связи выработки и затрат на заработную плату и себестоимости продукции проводим комбинационную группировку. Для проведения комбинационной группировки нужно воспользоваться интервальными рядами (см. приложения 5 и 6).Об этом свидетельствуют данные (см. приложение 7) себестоимость продукции в зависимости от выработки и затрат на заработную плату.

Данные комбинационной группировки свидетельствуют о прямолинейной и прямой связи между себестоимостью и выработкой. В разрезе групп с увеличением продуктивности от 265 до 334 шт. себестоимость повышается от 132,38р. До 450,46р. Между затратами на заработную плату и себестоимостью связь проявилась прямолинейная и прямая.

Дисперсия рассчитывается для того, чтобы изучить степень влияния факторов на отклонение эффективности выпуска в разрезе групп и подгрупп. В нашем случае рассчитываем среднюю внутригрупповую, межгрупповую, общую дисперсии и эмпирическое корреляционное отношение. Все эти показателя рассчитываем по данным (приложение7).

Межгрупповая дисперсия

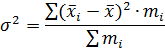
где - средняя себестоимость по группам наблюдений;

- средняя себестоимость по всей совокупности наблюдений;

- наименование по группам наблюдений.

Межгрупповая дисперсия, равная 33042,06р. показывает, что различия в величине

себестоимости продукции по группам составляют в среднем ±181,77р.

Внутригрупповая дисперсия

где - себестоимость в подгруппах;

- средняя себестоимость в группах;

-наименование по группам наблюдений.

Средняя из внутригрупповых дисперсий

По всем трем группам от неучтенных факторов по подгруппам вариация себестоимости составляет ±91,87р.

Общая дисперсия

Эмпирическое корреляционное отношение

 

Связь между себестоимостью изделия и рассматриваемыми факторами проявилась сильная, т.е. себестоимость зависит от факторов на 79,65%.

Средняя величина – это обобщающая характеристика единиц совокупности по определенному признаку. Средняя величина обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. При определении средних величин необходимо придерживаться общих принципов:

1.Исходить из качественного содержания осредненного признака, учитывая взаимосвязь признаков;

2.Нужно учитывать имеющиеся для расчета данные;

3.Средняя величина должна рассматриваться по однородной совокупности;

4.Общие средние величины должны подкрепляться групповыми средними;

5.Необходим обоснованный выбор единицы совокупности, в которой рассчитывается средняя.

Для определения средней себестоимости продукции необходимо воспользоваться формулой средней гармонической взвешенной:

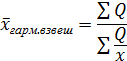
где Q – затраты на производство

x – себестоимость, р.

 

Затраты на производство и себестоимость продукции

Таблица 3.2.

 

Год	Затраты на производство, тыс. р.	Себестоимость, р.
	17626,707	68,56
	19311,450	71,23
	20049,770	75,02
	50926,848	186,63
	72430,248	246,41
	144613,691	391,22
	234954,294	530,11
	221687,222	484,14
	160377,192	342,23
	317989,859	676,77
Всего	1259967,281	352,78

 

Мода (Мо) – это наиболее распространенное значение признака, т.е. варианта, которая в ряду распределения имеет наибольшую частоту. В дискретном ряду мода определяется визуально. На основании таблицы 3.4 можно утверждать, что Мо=676,77р. (2013г), т.к. 2011г самый большой валовой выпуск продукции. Медиана (Ме) – варианта, которая расположена в середине упорядоченного ряда распределения и делит ряд на две равные по объему части. Медиана, как и мода не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами. В дискретном ряду медианой будет значение признака, для которого кумулятивная частота (Sm) равна или превышает половину объема совокупности. Объем совокупности, если судить по таблице 3.4, равен 3571543тыс.шт., его половина равна 1785771,5 тыс.шт. Кумулятивная частота 2008 года (Sm=2175156) превышает и максимально близка к этой цифре. Значит, медианой является себестоимость 2010 года и равняется Ме=530,11р. Следовательно, кумулятивная частота определяет, что валовой выпуск, равный 1785771,5 тыс.шт., будут иметь себестоимость в среднем 530,11р.

Коэффициент асимметрии равняется: , где

- средняя величина;

- мода;

- среднее квадратическое отклонение.

значит, имеется сильная левосторонняя асимметрия.

Показатели вариации

Вариация – различия в значениях какого-либо признака. Средняя величина дает только обобщающую характеристику совокупности, но не раскрывает строение совокупности, т.е. не показывает, как располагаются около средней варианты усредняемого признака. Для измерения и оценки вариации используются абсолютные (вариационный размах, среднее линейное и квадратическое отклонения, дисперсии) и относительные (коэффициенты вариации, неравномерности, локализации, концентрации) характеристики.

Вариационный размах (R) – характеризует диапазон вариации

-68,56=608,21

Среднее линейное отклонение:

Среднее квадратическое отклонение:

Дисперсия:

На основании среднего квадратического отклонения получим коэффициент вариации:

Себестоимость отклоняется от совокупности на 207,70р. или на 58,88%.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: