Расчет с помощью законов кирхгофа

 

Этот метод наиболее универсален и применяется для расчета любых цепей. при расчете этим методом первоначально определяются токи в ветвях, а затем напряжения на всех элементах. токи находятся из уравнений, полученных с помощью законов кирхгофа. так как в каждой ветви цепи протекает свой ток, то число исходных уравнений должно равняться числу ветвей цепи. число ветвей принято обозначать через n. часть этих уравнений записываются по первому закону кирхгофа, а часть – по второму закону кирхгофа. все полученные уравнения должны быть независимыми. это значит, чтобы не было таких уравнений, которые могут быть получены путем перестановок членов в уже имеющемся уравнении или путем арифметических действий между исходными уравнениями. при составлении уравнений используются понятия независимых и зависимых узлов и контуров. рассмотрим эти понятия.

независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. если число узлов обозначим через к, то число независимых узлов равно (к –1). на схеме (рис. 1.16) из двух узлов только один независим.

независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. в противном случае такой контур называется зависимым.

если число ветвей цепи равно n, то число независимых контуров равно [ n – (к –1)].

в схеме (рис. 1.16) всего три контура, но только два независимых контура, а третий – зависим. выделять независимые контура можно произвольно, т. е. в качестве независимых контуров можно выбрать при первом расчете одни, а при втором расчете (повторном) – другие, которые раньше были зависимыми. результаты расчета будут одинаковыми.

если по первому закону кирхгофа составить уравнения для (к –1) независимых узлов, а по второму закону кирхгофа составить уравнения для [ n – (к –1)] независимых контуров, то общее число уравнений будет равно:

(K –1) + [ n – (K –1)] = n.

Это означает, что для расчёта имеется необходимое число уравнений.

 

Последовательность расчёта:

1. Расставляем условно – положительные направления токов и напряжений.

2. Определяем число неизвестных токов, которое равно числу ветвей (n).

3. Выбираем независимые узлы и независимые контура.

Рис. 1.17. Пример расчета методом контурных токов

4. С помощью первого закона Кирхгофа составляем (К –1) уравнений для независимых узлов.

5. С помощью второго закона Кирхгофа составляем [ n – (К –1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них.

6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.

7. Определяем падения напряжений на всех элементах схемы.

Рассмотрим последовательность расчета на примере схемы, приведенной на рис. 1.16. Учитывая направление источника E, расставляем условно–положительные направления токов и напряжений. В схеме три ветви, поэтому нам необходимо составить три уравнения. В схеме два узла, следовательно, из них только один независимый. В качестве независимого узла выберем узел 1. Для него запишем уравнение по первому закону Кирхгофа:

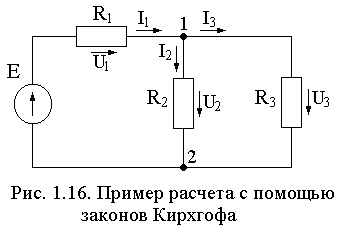I ₁ = I ₂ + I ₃.

Далее необходимо составить два уравнения по второму закону Кирхгофа. В схеме всего три контура, но независимых только два. В качестве независимых контуров выберем контур из элементов E – R ₁– R ₂ и контур из элементов R ₂– R ₃. Обходя эти два контура по направлению движения часовой стрелки, записываем следующие два уравнения:

E = I ₁, R ₁ + I ₂ R ₂,

0 = – I ₂ R ₂ + I ₃ R ₃ .

Решаем полученные три уравнения и определяем токи в ветвях. Затем через найденные токи по закону Ома определяем падения напряжений на всех элементах цепи.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: