 |
Применение функции комплексного переменного для представления синусоидальных токов и напряжений. векторная диаграмма, комплексное сопротивление, треугольник сопротивления
|
|
|
|
При расчете электрической цепи используются гармонические функции sin – ой или cos–ой формы. Так переменное напряжение в sin–ой форме может иметь вид:
(2.1)
Переменный ток в cos–ой форме имеет вид:
(2.2)
где U m, I m– амплитуды напряжения и тока, j U, j I – начальные (при t = 0) фазы напряжения и тока, w – круговая частота.
Несмотря на относительную простоту этих функций, аналитические операции над ними и графическое представление на одном графике несколько таких функций вызывает определенные сложности.
От этих сложностей свободен метод комплексных амплитуд, предложенный американскими инженерами А. Е. Кеннели и П. Ч. Штейнметцом в 1893–1894 гг.
Он основан на том, что показательная функция от комплексного аргумента j j обладает периодичностью. На основе формулы Эйлера имеем:
.
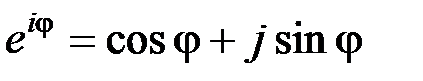Введем понятие комплексного напряжения:
(2.3)
Видно, что мнимая часть комплексного выражения полностью совпадает с переменным напряжением в sin–ой форме (2.1). Сразу отметим, что если бы переменное напряжение было представлено в cos–ой форме, то оно совпало бы с вещественной частью комплексного напряжения.
Введем понятие комплексного тока:
(2.4)
Здесь вещественная часть комплексного выражения совпадает с переменным током в cos–ой форме (2.2). Если бы в (2.2) была sin–ая форма, то она совпала бы с мнимой частью комплексного тока.
Было предложено периодический сигнал представлять в комплексной форме (2.3), (2.4). Так как вещественная часть комплексного сигнала имеет cos–ый характер, то целесообразно исходные сигналы записывать в cos–ой форме (в принципе cos–ая и sin–ая функции отличаются только фазой).
Возникает мысль, что тогда в процессе анализа необходимо все время подчеркивать, что в комплексном токе или напряжении учитывается только вещественная составляющая. Однако, в процессе анализа этого делать нет необходимости, а делается это только в конце анализа в результатах расчета.
|
|
|
Итак, в методе комплексных амплитуд исходное переменное напряжение в начале записывается в cos–ой форме:
.
Затем это напряжение представляется в комплексной форме:
(2.5)
В такой форме записываются напряжения и токи цепи, выполняется анализ, получается результат в комплексной форме, вещественная часть которого и будет действительным результатом.
Запишем комплексное напряжение и комплексный ток:
,
Здесь 
и 
называются комплексными амплитудами напряжения и тока и обозначаются:
;
(2.6)
Комплексные амплитуды напряжения и тока – это значение комплексных напряжения и тока при t = 0.
Всякая комплексная величина может быть представлена вектором на комплексной плоскости. Если аргумент комплексной величины зависит от времени, например (2.5), то на комплексной плоскости эта величина должна представляться вектором, вращающимся против часовой стрелки (положительное направление вращения) с частотой ω. Реально отобразить это на комплексной плоскости не возможно. Поэтому такая комплексная величина на комплексной плоскости представляется в виде вектора при
t = 0. На рис. 2.1 показаны вектора напряжения и тока в комплексной форме на комплексной плоскости.
Комплексная плоскость, на которой представлены вектора комплексных напряжений и токов называется векторной диаграммой.
Законы Кирхгофа для комплексных токов имеют такую же трактовку, как и для цепей постоянного тока. В цепях переменного тока помимо резисторов большую роль играют реактивные элементы – конденсаторы и катушки индуктивности. Они так же формируют сопротивление цепи. При использовании комплексных напряжений и токов вводится понятие комплексного сопротивления, которое обозначается 
. Закон Ома в комплексной форме имеет вид:
|
|
|
(2.7)
Как всякая комплексная величина, комплексное сопротивление cо 
стоит из вещественной и мнимой частей:
(2.8)
Вещественная часть R комплексного сопротивления цепи переменного тока включает резистивные (диссипативные) составляющие цепи. Мнимая часть X комплексного сопротивления переменного тока включает реактивные составляющие цепи. Поэтому она называется чаще реактивной составляющей комплексного сопротивления. Если вещественная часть комплексного сопротивления всегда положительная, то реактивная часть может быть положительной (X >0) или отрицательной (X <0).
Комплексное сопротивление иногда удобно представлять в тригонометрической и показательной формах:
(2.9)
где 
; 
.
Комплексное сопротивление может быть представлено на комплексной плоскости (рис. 2.2) в виде отрезка 
, проведенного под углом jZ к вещественной оси.
Проекции комплексного сопротивления на оси комплексной плоскости, соединенные в виде треугольника, создают треугольник сопротивлений. Из треугольника сопротивления можно получить выражения для модуля и фазы сопротивления (2.9), а так же косинусоидальную и синусоидальную составляющие в тригонометрической форме представления комплексного сопротивления.
ОПРЕДЕЛЕНИЯ
Добротностью называется отношение амплитуды реактивной мощности цепи к величине средней мощности.
Затуханием называется величина, обратная добротности, и обозначается через d.
Резистивным двухполюсником называется двухполюсник, содержащий только резистивные элементы. Простейшим примером такого двухполюсника является резистор
Емкостной двухполюсник представляет собой конденсатор, к которому приложено напряжение.
Индуктивный двухполюсник представляет собой катушку индуктивности, к которой приложено напряжение.
Идеальный индуктивный двухполюсник характеризуется отсутствием явления диссипации, т. е. в нем не происходит рассеивание мощности.
Мгновенная мощность идеального индуктивного двухполюсника определяется по формуле 
при 
:
|
|
|
