 |
Указания к решению задач 31-60
|
|
|
|
Эти задачи относятся к теме «Однофазные электрические цепи переменного тока». Перед решением необходимо изучить физические процессы, протекающие в неразветвленных цепях переменного тока с активным сопротивлением, индуктивностью и емкостью. Знать формулы для расчета таких цепей. Ознакомиться с методикой построения векторных диаграмм.
Перед решением рассмотрите типовые примеры:
В неразветвленной цепи переменного тока с активными и реактивными сопротивлениями определить полное сопротивление цепи; ток в цепи; коэффициент мощности; активную, реактивную и полную мощности цепи. Построить в масштабе векторную диаграмму и описать ее построение.
| ~ |
| XL1 |
| XL2 |
| R1 |
| R2 |
| XC1 |
| XC2 |
| Дано: R1= 2 Ом R2= 2 Ом ХL1 = 4 Ом XL2 = 5 Ом XC1 = 4 Ом XC2 = 2 Ом U = 220 В | Решение
1. Находим полное сопротивление цепи:
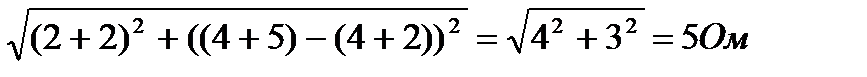2. По закону Ома для цепи переменного тока определим ток в цепи
|
| Z, I, cosj, P, Q, S | 
3. Коэффициент мощности
|
|
значит угол сдвига фаз j=36050’
4. Активная мощность
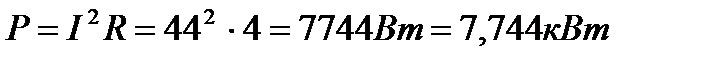или
Реактивная мощность
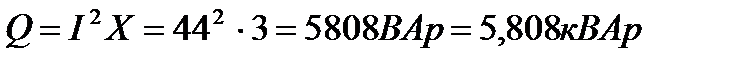или
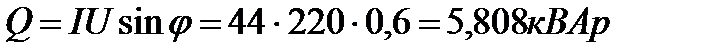
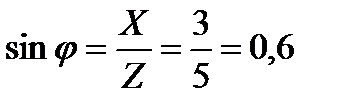
Полная мощность
или
При построении векторной диаграммы следует исходить из условий:
1. ток одинаков для любого участка цепи, так как в ней нет разветвлений
2. на каждом сопротивлении при прохождении тока создается падение напряжения, которое определяют по закону Ома для участка цепи.
Построение векторной диаграммы:
1. Вычислим падения напряжения на участках цепи
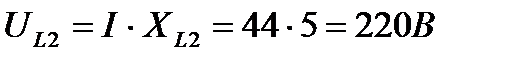
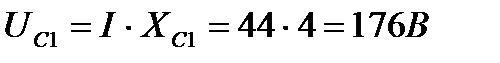
2. Задаемся масштабом по току и напряжению
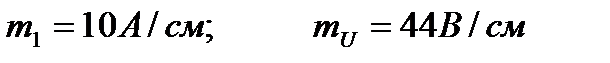
Тогда длины векторов будут следующие:
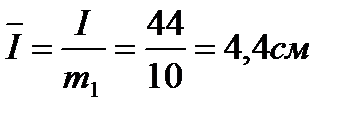
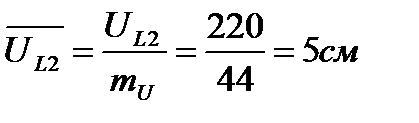
3. Откладываем вектор тока 
в масштабе на оси абсцисс
4. Далее откладываем векторы напряжений на каждом сопротивлении с учетом сдвига фаз относительно вектора тока . При этом целесообразно придерживаться последовательности расположения сопротивлений и напряжений на них:
|
|
|
| UR2 |
| UL2 |
| UC2 |
| UR1 |
| UC1 |
| UL1 |
| U |
| φ |
| I |
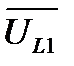откладываем из начала вектора тока под углом 900 в сторону опережения этого вектора (вверх)
б) из конца вектора 
отложим вектор напряжения на активном сопротивлении 
параллельно вектору тока, так как они совпадают по фазе
в) из конца вектора отложим вектор напряжения на индуктивном сопротивлении 
в сторону опережения (вверх) на 900 относительно вектора тока.
г) из конца вектора 
отложим вектор напряжения 
параллельно вектору тока, так как они совпадают по фазе
д) из конца вектора 
отложим вектора напряжений на емкостных сопротивлениях 
и 
в сторону отставания (вниз) на 900 относительно вектора тока.
е) соединим начало первого вектора с концом последнего 
и получим вектор общего, приложенного к цепи напряжения 
и угол сдвига фаз φ.
Проверка
Следует проверить аналитическое решение построение векторной диаграммы путем их сопоставления следующим образом:
1. проверка угла φ производится с помощью транспортира и сравнением полученной величины с расчетным значением в решении, задачи. В заданном случае по расчету φ=36050’
2. проверка значения приложенного напряжения: по диаграмме длина вектора =5 см., значит 
, что соответствует условию задачи, значит диаграмма построена верно.
При значительных расхождениях следует найти ошибку.
Пример №3
Для заданной векторной диаграммы известны ток и напряжение на каждом сопротивлении. Определить характер и величину каждого сопротивления, вычислить приложенное напряжение, полное сопротивление цепи, активную, реактивную и полную мощности, а также величину индуктивности и емкости, если частота тока равна 50 Гц
| R1 |
| XL |
| XC |
| R2 |
| U4 |
| U3 |
| U |
| φ |
| U1 |
| U2 |
| I |
|
|
|
U1 = 20 B; U2 =20 B; U3 = 60 B; U4 = 10 B; I = 5 A
Решение
Из векторной диаграммы следует, что напряжение отстает от тока на угол 900. Следовательно, на первом участке включен конденсатор, сопротивление которого
Вектор напряжения на втором участке 
направлен параллельно вектору тока, то есть совпадает по фазе. Значит, на втором участке включено активное сопротивление
Вектор напряжения на третьем участке 
опережает вектор тока на угол 900, что характерно для индуктивности, сопротивление которой
На четвертом участке включено активное сопротивление
Из векторной диаграммы определим значение приложенного напряжения:
Полное сопротивление цепи
Активная, реактивная и полная мощности цепи:
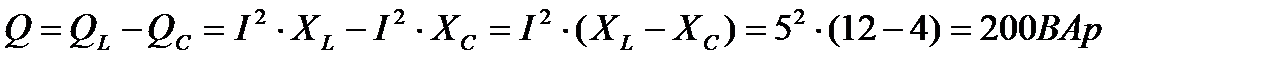
Индуктивность катушки:
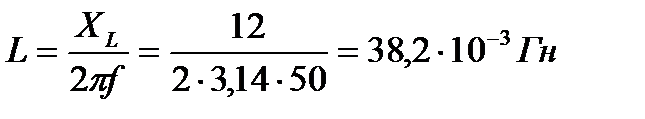
Емкость конденсатора:
|
|
|
