Расчет линейных размерных цепей методом полной

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО КУРСОВОЙ (контрольно-курсовой) РАБОТЕ

по дисциплине

 

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

 

ЧАСТЬ 2

РАСЧЕТ СБОРОЧНЫХ РАЗМЕРНЫХ ЦЕПЕЙ МЕТОДАМИ

ВЗАИМОЗАМЕНЯЕМОСТИ

При выполнении работы необходимо методами полной взаимозаменяемости и теоретико-вероятностным методом решить прямую и обратную задачи расчета сборочной размерной цепи.

 

Теоретические положения

Наиболее ответственным этапом в решении размерных цепей является выявление замыкающего размера, определение его поля допуска и выявление составляющих размеров размерной цепи.

После того, как выявлена размерная цепь, необходимо:

1) составить график размерной цепи,

2) составить уравнение размерной цепи,

3) подобрать метод достижения заданной точности замыкающего размера.

При составлении графика размерной цепи необходимо охватить все, входящие в нее размеры, образующие замкнутый контур. На графике все размеры размерной цепи обозначаются прописными буквами русского и строчными буквами греческого алфавитов с индексом.

Общий вид уравнения размерной цепи описывается выражением:

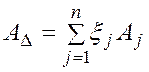(3.1)

где n – число составляющих размеров

- передаточное отношение между замыкающим размером и составляющим размером .

В размерных цепях с параллельными звеньями (линейные цепи)

.

В плоских и пространственных цепях (общий случай)

.

Передаточное отношение размеров размерных цепей учитывают степень и направленность влияния составляющих размеров на замыкающий размер.

В линейных размерных цепях передаточные отношения увеличивающихся размеров равны +1, уменьшающихся размеров равны –1.

При выборе метода достижения требуемой точности замыкающего размера (решения размерных цепей) рекомендуется в первую очередь использовать или метод полной взаимозаменяемости, или вероятностный метод, при которых сборка производится без подбора, подгонки и регулирования и собранные изделия отвечают всем требованиям взаимозаменяемости.

Метод полной взаимозаменяемости заключается в том, что требуемая точность замыкающего размера обеспечивается при любом сочетании размеров деталей, попавших в сборочный комплект.

При расчете размерных цепей методом полной взаимозаменяемости используются следующие зависимости:

, (3.2)

, (3.3)

, (3.4)

где и - номинальное значение замыкающего и j – го составляющего размеров;

и - среднее отклонение замыкающего и j – го составляющего размеров;

и 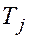- допуск замыкающего и j – го составляющего размеров;

Величина среднего отклонения связана со значениями верхнего и нижнего отклонений следующими уравнениями:

; (3.5)

для j-го составляющего размера

; (3.6)

Предельные значения замыкающего размера и определяются по выражению:

. (3.7)

Предельные отклонения замыкающего размера определяются по уравнениям:

; (3.8)

. (3.9)

Вероятностный метод расчета заключается в том, что требуемая точность замыкающего размера достигается не у всех, а у заранее обусловленной части сборок при любом сочетании размеров деталей, попавших в сборочный комплект.

При расчете размерных цепей вероятностным методом используют уравнение (3..2), а также

, (3.10)

(3.11)

где и - коэффициенты относительной ассиметрии законов распределения значений замыкающего и j – го составляющего размеров;

и - относительные средние квадратические отклонения законов распределения значений замыкающего и j – го составляющего размеров.

Если известны законы распределения составляющих размеров, то значения и можно определять по уравнениям

(3.12)

(3.13)

Численные значения a_j и l_j зависят от условий и масштаба производства и различны для различных категорий размеров, технологических операций и методов обработки.

В таблице 3.1 приведены для трех категорий размеров ориентировочные значения коэффициентов a_j и l_j.

 

Значения коэффициентов a_j и l_j Таблица 3.1

Категории размеров	aj	lj
Охватывающие (размеры отверстий)	(+0,25)…(-0,25)	0,37…0,47
Охватываемые (размеры валов)	(+0,3)…(-0,2)	0,33…0,47
Остальные (размеры, не относящиеся ни к валам, ни к отверстиям)	(+0,2)…(-0,2)	0,33…0,47
Примечания: 1. Значения aj рекомендуется принимать для охватываемых размеров положительные, для охватывающих – отрицательные, для остальных – равные нулю. 2. Значения lj рекомендуется принимать при более жестких допусках (Тj) ближе к верхнему пределу, а при расширенных допусках – ближе к нижнему пределу.

При проектных расчетах и при выполнении курсовой работы можно принимать следующие значения коэффициентов:

a_D = 0;

a_j = + 0,2 для охватываемых размеров (размеров валов);

a_j = - 0,2 для охватывающих размеров (размеров отверстий);

a_j = 0 для остальных размеров;

l_D = 0,333 при допустимом количестве брака на сборке равном 0,27%;

l_D = 0,333К₀ при допустимом количестве брака на сборке, отличающемся от 0,27%,

где коэффициент К₀ определяется по таблице 3.2;

l_j = 0,4 для всех видов размеров.

 

Значения коэффициентов К₀ Таблица 3.2

Допустимое количество брака, %	0,05	0,10	0,20	0,27	0,50	1,00	1,50	2,00	3,00	4,00	5,00
К0	0,86	0,91	0,97	1,00	1,06	1,16	1,23	1,29	1,38	1,46	1,52

 

Практически предельные значения замыкающего размера, ограничивающие область его значений, вероятностью попадания в которую задается заранее, определяются по уравнению 3.7.

Расчет линейных размерных цепей методом полной

Взаимозаменяемости

Прямая задача

При решении прямой задачи в качестве исходных данных задаются номинальный размер и предельные отклонения замыкающего размера, а также номинальные значения составляющих размеров.

В процессе решения задачи производят следующие действия:

1. По заданной величине предельных отклонений замыкающего размера вычисляют величину его допуска

и значение его среднего отклонения

,

а также предельные значения замыкающего размера

,

.

2. Составляют график размерной цепи.

3. Составляют уравнение размерной цепи.

4. Осуществляют проверку правильности назначения номинальных размеров по уравнению (3.2).

В том случае, когда проверка дает неудовлетворительные результаты, в номинальные размеры одного или нескольких составляющих размеров вносят необходимые коррективы.

5. Осуществляют увязку допусков замыкающего и составляющих размеров. Для этого допуск замыкающего размера Т_D распределяют между составляющими размерами. Одним из способов распределения допуска Т_D является способ одной степени точности, при котором принимают, что все составляющие размеры выполнены с одной степенью точности (одного квалитета). Этот способ рекомендуется применять при сильно отличающихся величинах номинальных размеров.

При способе одной степени точности ориентируются на среднюю степень точности (квалитет) составляющих звеньев а_С.

Величина а_С определяется выражением

, (3.14)

где Т_D - допуск замыкающего размера, мкм;

i_j - значение единицы допуска, мкм;

D - среднее геометрическое значение интервала размеров, мм.

Значения i для диапазона размеров до 630 мм (5…17 квалитетов) приведены в таблице 3.3.

Значение Таблица 3.3

Интервалы размеров, мм	До 3	св. 3 до 6	св. 6 до 10	св. 10 до 18
ij, мкм	0,55	0,73	0,90	1,08

 

Интервалы размеров, мм	св. 18 до 30	св. 30 до 50	св. 50 до 80	св. 80 до 120
ij, мкм	1,31	1,56	1,86	2,17

 

Интервалы размеров, мм	св. 120 до 180	св. 180 до 250	св. 250 до 315
ij, мкм	2,52	2,89	3,22

 

Интервалы размеров, мм	св. 315 до 400	св. 400 до 500	св. 500 до 630
ij, мкм	3,54	3,89	4,34

Если в размерную цепь в качестве составляющих звеньев входят стандартные (покупные детали и изделия, например, подшипники качения, муфты, электродвигатели и др., то их допуски для рассчитываемой размерной цепи являются заданными и тогда уравнение для определения величины а_С будет иметь вид

, (3.15)

где T_cm - допуски стандартных изделий, мкм;

m - число стандартных деталей с заданными допусками.

В размерных цепях, в состав которых входит ширина колец подшипников качения, допуск на ширину следует брать в зависимости от диаметра посадочного отверстия d и класса точности подшипника.

В узлах, используемых в качестве заданий для расчета размерных цепей, применяются подшипники нулевого класса с размерами d, лежащими в пределах от 2,5 до 50 мм. Для таких подшипников допуск ширины равен 0,12 мм.

6. Вычисленное по формулам (3.14) или (3.15) значение а_С сопоставляют с числом единиц допуска по квалитетам (прил. А) и приближенно определяют среднюю степень точности (квалитет) составляющих размеров цепи и их допуски.

Так как полученное значение а_С может не совпадать ни с одним табличным значением, то можно использовать допуски различных квалитетов, учитывая технологические условия.

7. Осуществляют проверку правильности назначения допусков. Критерием правильности назначения допусков служит уравнение (4), которое должно удовлетворяться. В случае, если условие (4) не удовлетворяется, то на один из составляющих размеров (называемый увязочным) А_х назначают нестандартный допуск, определяемый как .

8. При этом, если , то приходится ужесточать допуск Т_х на увязочный размер; если , то можно расширить допуск Т_х увязочного размера.

Если же на все размеры необходимо назначить стандартные допуски, то допустимо, чтобы Т_D превышало не более чем на 5…6%.

При назначении допусков рекомендуется на охватывающие размеры назначать допуски с основным отклонением Н, т.е. использовать поля Н5, Н6, …, Н17; на охватываемые размеры назначать допуски с основным отклонением h, т.е. использовать поля h5, h6, …, h17; на остальные размеры назначать допуски с основным отклонением JS, т.е. использовать поля JS5, JS6, …, JS17.

9. Осуществляют увязку средних отклонений замыкающего и составляющего размеров. Для этого, исходя из назначенных полей допусков, выбирают предельные отклонения (E_s, E_i) всех составляющих размеров, кроме увязочного, а затем по выражению (35) находят средние отклонения Е_с для каждого составляющего размера.

Среднее отклонение увязочного размера определяют исходя из выражения (3), а его предельные отклонения – исходя из выражений (3.8) и (3.9).

Правильность найденных отклонений увязочного размера может быть проверена по формуле

,

где Т_х – допуск увязочного размера, который был установлен при распределении допуска замыкающего размера.

Обратная задача

При решении обратной задачи заданы номинальные значения и предельные отклонения всех составляющих размеров, полученных в результате решения прямой задачи.

Процесс решения заключается в том, что по исходным данным составляющих размеров вычисляют номинальное значение N_D, среднее отклонение E_CD и допуск Т_D замыкающего размера, а также его предельные размеры A_Dmax, A_Dmin и отклонения E_SD, E_iD.

Для вычисления указанных величин следует воспользоваться выражениями (3.2)…(3.3), (3.7).

После вычисления величин A_Dmax, A_Dmin производят сравнение их с заданными значениями замыкающего размера. При этом должны обеспечиваться условия:

(3.16)

Если условия (3.16) не выполняются, то результаты можно считать удовлетворительными при

,

и .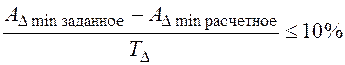

В противном случае необходимо откорректировать исходные величины составляющих размеров, т.е. решить прямую задачу.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: