Значение передаточных отношений

Обозначение передаточных отношений	x1	x2	x3	x4	x5	x6
Численные значения xi	–1	+1	+1	–1	–1	–1

 

4. Проведем проверку правильности назначения номинальных значений составляющих размеров.

N_D=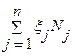

N_D= –12 +1+105 –15 –64 –15= 0.

Так как по условию задачи N_D=0, следовательно, номинальные размеры назначены правильно.

5. Осуществим увязку допусков, для чего исходя из величины Т_r рассчитаем допуски составляющих размеров.

Так как в узел входят подшипники качения, допуски которых являются заданными, то для определения величины а_с воспользуемся следующей зависимостью.

Допуск ширины подшипников равен 0,12 мм, то есть

Т₄ = Т₆ = 0,12 мм.

Следовательно

, где Т_сm – допуски стандартных деталей, мкм;

m – число стандартных деталей с заданным допуском.

Значения i_j берутся из табл. 3 методических указаний.

а_с = (800 – 2×120)/(1,08+0,55+2,17+1,86)» 99;

6. По приложению А устанавливаем, что такому значению а_с соответствует точность, лежащая между 10 и 11 квалитетами.

Примем для всех размеров 11 квалитет, тогда

T₁ = 0,11 мм; T₂ = 0,06 мм; T₃ = 0,22 мм; T₅ = 0,19 мм.

7. Произведем проверку правильности назначения допусков составляющих размеров по уравнению:

,

= 0,11+0,06+0,22+0,19+0,12+0,12= 0,82 мм.

Полученная сумма допусков превышает на величину равную 0,02, что составляет»2% от Т_r. Следовательно, допуски можно оставить без изменения.

8. Осуществим увязку средних отклонений, для чего примем следующий характер расположения полей допусков составляющих размеров.

A₁ = 12JS11 (±0,055) мм, A₂ = 1h11 (_-0,06) мм,

A₃ = 105JS11 (±0,11) мм, A₄ = A₆ = 15_{-0,12 мм}

A₅ = 64h11 (_-0,19) мм.

Сведем данные для расчета в таблицу:

Таблица расчета данных

Обозначение размера	Размер	xi	Eci	xiEci
А1	12JS11 (±0,055)	–1
А2	1h11 (-0,06)	+1	–0,03	–0,03
А3	105JS11 (±0,11)	+1
А4	15-0,12	–1	–0,06	+0,06
А5	64h11 (-0,19)	–1	–0,095;(Ec`5)	+0,095;(–Ec`5)
А6	15-0,12	–1	–0,06	+0,06

 

Из уравнения

найдем среднее отклонение замыкающего размера и сравним его с заданным

E_cr = 0–0,03+0+0,06+0,095+0,06 = +0,185 мм.

Так как полученное значение не совпадает с заданным, то произведем увязку средних отклонений за счет среднего отклонения размера А₅, принятого в качестве увязочного.

Величину среднего отклонения размера А₅ найдем из уравнения:

+0,4 =–0,03+0+0,06 –Еc`₅+0,06.

Откуда Еc`₅= –0,31 мм.

Предельные отклонения размера А₅:

ЕS`<sub>5</sub> = Еc`₅ + 0,5×Т₅ = –0,31+ 0,5×0,19= – 0,215 мм,

ЕI`<sub>5</sub> = Еc`₅ – 0,5×Т₅ = –0,31 – 0,5×0,19= – 0,405 мм.

Таким образом А`₅ = мм.

Задача 2 (обратная задача)

Найти предельные значения замыкающего размера А_r при значениях составляющих размеров, полученных в результате решения задачи 1. Расчет произвести методом полной взаимозаменяемости.

Сведем данные для расчета в таблицу

Таблица расчета данных

Обозначение размера	Размер	xj	Nj	Ecj	Tj	xjNj	xjEcj	½xj½Tj
А1	12JS11 (±0,055)	–1			0,11	–12		0,11
А2	1h11 (-0,06)	+1		–0,03	0,06	+1	–0,03	0,06
А3	105JS11 (±0,11)	+1			0,22	+105		0,22
А4	15-0,12	–1		–0,06	0,12	–15	+0,06	0,12
А5	64h11 (-0,19)	–1		–0,31	0,19	–64	+0,31	0,19
А6	15-0,12	–1		–0,06	0,12	–15	+0,06	0,12

 

1. Номинальное значение замыкающего размера:

N_D=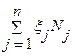

N_D= –12 +1+105 –15 –64 –15= 0.

2. Среднее отклонение замыкающего размера:

Е_сr =0–0,03+0+0,06+0,31+0,06= +0,4.

3. Допуск замыкающего размера:

Т_r =0,11+0,06+0,22+0,19+0,12+0,12= 0,82 мм.

Полученная сумма допусков превышает заданную на величину равную 0,02, что составляет»2% от Т_r. Следовательно, допуски можно оставить без изменения.

4. Предельные отклонения замыкающего размера:

А_rmax =N_r + Ec_r + 0,5×T_r= 0+0,4+0,5×0,82= 0,81 мм;

А_rmin = N_r + Ec_r – 0,5×T_r= 0+0,4 – 0,5×0,82= –0,01 мм

5. Сравниваем полученные результаты с заданными:

А_{r max расч.} =0,81 > А_{rmax зад.} = 0,8

А_{rmin расч.} = –0,01< А_rminзад. = 0

Т.к условия не выполняются, то осуществим проверку допустимости расчетных значений А_rмах и А_rмin.

(А_{r max расч.} – А_{r max зад.})/ Т_r = (0,81–0,8)/0,8» 0,0125 =1,25%

(А_{rmin зад.} – А_{rmin расч.})/ Т_r = (0 – (–0,01))/0,8» 0,0125 = 1,25%

Полученные значения не превышают установленных 10%. Следовательно, изменения предельных отклонений составляющих размеров не требуется.

 

Задача 3 (прямая задача)

Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера, равное

А = 0^+0,8

Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%.

На детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров.

N_А1 = 12 мм; N_А2 = 1 мм; N_А3 = 105 мм; N_А4 = 15 мм; N_А5 = 64 мм; N_А6 = 15 мм;

А_D= 0^+0,8.

1. Согласно заданию:

N_D= 0 мм.

Т _D =ES_D – EI_D = +0,8 – 0 = 0,8 мм.

E_сD = (ES_D + EI_D)/2 = (+0,8 + 0)/2 = +0,4 мм.

А_Dmax = N_D + ES_D = 0+0,8= 0,8 мм.

А_Dmin = N_D + EI_D = 0 + 0 = 0 мм

2. Составим график размерной цепи:

 

3. Составим уравнение размерной цепи:

A_D=

A_D = x₁A₁ + x₂A₂ + x₃A₃ + x₄A₄ + x₅A₅+ x₆A₆.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: