 |
Дискриминантные функции и их геометрическая интерпретация
|
|
|
|
Содержание
Введение
1. Дискриминантные функции и их геометрическая интерпретация
2. Расчет коэффициентов дискриминантной функции
3. Классификация при наличии двух обучающих выборок
4. Классификация при наличии k обучающих выборок
5. Взаимосвязь между дискриминантными переменными и дискриминантными функциями
Заключение
Список использованной литературы
Введение
Д u скр u м u нантный анализ - это раздел математической статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам. Например, разбиение совокупности предприятий на несколько однородных групп по значениям каких-либо показателей производственно-хозяйственной деятельности.
Методы дискриминантного анализа находят применение в различных областях: медицине, социологии, психологии, экономике и т.д. При наблюдении больших статистических совокупностей часто появляется необходимость разделить неоднородную совокупность на однородные группы (классы). Такое расчленение в дальнейшем при проведении статистического анализа дает лучшие результаты моделирования зависимостей между отдельными признаками.
Дискриминантный анализ оказывается очень удобным и при обработке результатов тестирования отдельных лиц. Например, при выборе кандидатов на определенную должность можно всех опрашиваемых претендентов разделить на две группы: «подходит» и «не подходит».
Можно привести еще один пример применения дискриминантного анализа в экономике. Для оценки финансового состояния своих клиентов при выдаче им кредита банк классифицирует их на надежных и не надежных по ряду признаков. Таким образом, в тех случаях, когда возникает необходимость отнесения того или иного объекта к одному из реально существующих или выделенных определенным способом классов, можно воспользоваться дискриминантным анализом.
|
|
|
Аппарат дискриминантного анализа разрабатывался многими учеными-специалистами, начиная с конца 50-х годов ХХ в. Дискриминантным анализом, как и другими методами многомерной статистики, занимались П.Ч. Махаланобис, Р. Фишер, Г.Хотеллинг и другие видные ученые.
Все процедуры дискриминантного анализа можно разбить на две группы и рассматривать их как совершенно самостоятельные методы. Первая группа процедур позволяет интерпретировать различия между существующими классами, вторая - проводить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат.
Пусть имеется множество единиц наблюдения - генеральная совокупность. Каждая единица наблюдения характеризуется несколькими признаками (переменными)  - значение j -й переменной у i -го объекта i =1,…N; j=1,…p.
- значение j -й переменной у i -го объекта i =1,…N; j=1,…p.
Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом 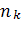 , где k - номер подмножества (класса), k = 1,..., q.
, где k - номер подмножества (класса), k = 1,..., q.
Признаки, которые используются для того, чтобы отличать один класс (подмножество) от другого, называются дискриминантными переменными. Каждая из этих переменных должна измеряться либо по интервальной шкале, либо по шкале отношений. Интервальная шкала позволяет количественно описать различия между свойствами объектов. Для задания шкалы устанавливаются произвольная точка отсчета и единица измерения. Примерами таких шкал являются календарное время, шкалы температур и т. п. В качестве оценки положения центра используются средняя величина, мода и медиана.
Шкала отношений - частный случай интервальной шкалы. Она позволяет соотнести количественные характеристики какого-либо свойства у разных объектов, например, стаж работы, заработная плата, величина налога.
|
|
|
Теоретически число дискриминантных переменных не ограничено, но на практике их выбор должен осуществляться на основании логического анализа исходной информации и одного из критериев, о котором речь пойдет немного ниже. Число объектов наблюдения должно превышать число дискриминантных переменных, как минимум, на два, т. е. р < N. Дискриминантные переменные должны быть линейно независимыми. Еще одним предположением при дискриминантном анализе является нормальность закона распределения многомерной величины, т.е. каждая из дискриминантных переменных внутри каждого из рассматриваемых классов должна быть подчинена нормальному закону распределения. В случае, когда реальная картина в выборочных совокупностях отличается от выдвинутых предпосылок, следует решать вопрос о целесообразности использования процедур дискриминантного анализа для классификации новых наблюдений, так как в этом случае затрудняются расчеты каждого критерия классификации.
Дискриминантные функции и их геометрическая интерпретация
Перед тем как приступить к рассмотрению алгоритма дискриминантного анализа, обратимся к его геометрической интерпретации. На рис. 1 изображены объекты, принадлежащие двум различным множествам М1 и М2.

Рис.1 Геометрическая интерпретация дискриминантной функции и дискриминантных переменных
Каждый объект характеризуется в данном случае двумя переменными 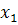 и
и  .Если рассматривать проекции объектов (точек) на каждую ось, то эти множества пересекаются, т.е. по каждой переменной отдельно некоторые объекты обоих множеств имеют сходные характеристики. Чтобы наилучшим образом разделить два рассматриваемых множества, нужно построить соответствующую линейную комбинацию переменных
.Если рассматривать проекции объектов (точек) на каждую ось, то эти множества пересекаются, т.е. по каждой переменной отдельно некоторые объекты обоих множеств имеют сходные характеристики. Чтобы наилучшим образом разделить два рассматриваемых множества, нужно построить соответствующую линейную комбинацию переменных 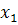 и
и  . Для двумерного пространства эта задача сводится к определению новой системы координат. Причем новые оси L и С должны быть расположены таким образом, чтобы проекции объектов, принадлежащих разным множествам на ось L, были максимально разделены. Ось С перпендикулярна оси L и разделяет два «облака» точек наилучшим образом, Т.е. чтобы множества оказались по разные стороны от этой прямой. При этом вероятность ошибки классификации должна быть минимальной. Сформулированные условия должны быть учтены при определении коэффициентов
. Для двумерного пространства эта задача сводится к определению новой системы координат. Причем новые оси L и С должны быть расположены таким образом, чтобы проекции объектов, принадлежащих разным множествам на ось L, были максимально разделены. Ось С перпендикулярна оси L и разделяет два «облака» точек наилучшим образом, Т.е. чтобы множества оказались по разные стороны от этой прямой. При этом вероятность ошибки классификации должна быть минимальной. Сформулированные условия должны быть учтены при определении коэффициентов  и
и  следующей функции:
следующей функции:
|
|
|
F(x) = 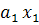 +
+ 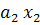 (1)
(1)
Функция F(x) называется канонической дискриминантной функцией, а величины  и
и  - дискриминантными переменными.
- дискриминантными переменными.
Обозначим  - среднее значение j -го признака у объектов i -го множества (класса). Тогда для множества М1 среднее значение функции
- среднее значение j -го признака у объектов i -го множества (класса). Тогда для множества М1 среднее значение функции  (x) будет равно:
(x) будет равно:
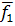 (x) =
(x) = 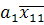 +
+  ; (2)
; (2)
Для множества М2 среднее значение функции  равно:
равно:
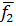 (x) =
(x) =  +
+  ; (3)
; (3)
Геометрическая интерпретация этих функций - две параллельные прямые, проходящие через центры классов (множеств) (рис.2).

Рис. 2. Центры разделяемых множеств и константа дискриминации
Дискриминантная функция может быть как линейной, так и нелинейной. Выбор ее вида зависит от геометрического расположения разделяемых классов в пространстве дискриминантных переменных. Для упрощения выкладок в дальнейшем рассматривается линейная дискриминантная функция.
|
|
|


