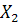|
Классификация при наличии двух обучающих выборок
|
|
|
|
Перед тем как приступить непосредственно к процедуре классификации, нужно определить границу, разделяющую в частном случае две рассматриваемые группы. Такой величиной может быть значение функции, равноудаленное от  и
и 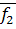 , т.е.
, т.е.
 (16)
(16)
Величина С называется константой дискриминации.
На рис.1 видно, что объекты, расположенные над прямой f(x)= 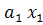 +
+ 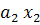 +…+
+…+  =C, находятся ближе к центру множества
=C, находятся ближе к центру множества 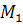 и, следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой прямой, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами выбрана так, как сказано выше, то суммарная вероятность ошибочной классификации минимальная.
и, следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой прямой, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами выбрана так, как сказано выше, то суммарная вероятность ошибочной классификации минимальная.
Рассмотрим пример использования дискриминантного анализа для проведения многомерной классификации объектов. При этом в качестве обучающих будем использовать сначала две выборки, принадлежащие двум классам, а затем обобщим алгоритм классификации на случай k классов.
Пример 1. Имеются данные по двум группам промышленных предприятий машиностроительного комплекса:
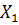 -фондоотдача основных производственных фондов, руб.;
-фондоотдача основных производственных фондов, руб.;
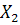 -затраты на рубль произведенной продукции, коп.;
-затраты на рубль произведенной продукции, коп.;
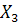 -затраты на сырье и материалов на один рубль продукции, коп.
-затраты на сырье и материалов на один рубль продукции, коп.
| Номер | Х 1 | Х 2 | ХЗ | |
| предприятия | ||||
| 1 | 0,50 | 94,0 | 8,50 | |
| l-я группа | 2 | 0,67 | 75,4 | 8,79 |
| 3 | 0,68 | 85,2 | 9,10 | |
| 4 | 0,55 | 98,8 | 8,47 | |
| 5 | 1,52 | 81,5 | 4,95 | |
| 2-я группа | 6 | 1,20 | 93,8 | 6,95 |
| 7 | 1,46 | 86,5 | 4,70 |
Необходимо провести классификацию четырех новых предприятий, имеющих следующие значения исходных переменных:
l-е предприятие: 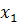 = 1,07,
= 1,07, 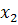 =93,5,
=93,5, 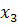 =5,30,
=5,30,
2-е предприятие:  = 0,99,
= 0,99, 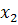 =84,0,
=84,0, 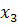 =4,85,
=4,85,
3-е предприятие: 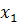 = 0,70,
= 0,70, 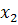 =76,8,
=76,8, 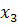 =3,50,
=3,50,
4-е предприятие: 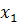 = 1,24,
= 1,24, 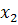 =88,0,
=88,0, 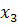 =4,95.
=4,95.
|
|
|
Для удобства запишем значения исходных переменных для каждой группы предприятий в виде матриц 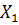 и
и 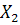 :
:
 (17)
(17)
Рассчитаем среднее значение каждой переменной в отдельных группах для определения положения центров этих групп:
I гр. 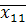 =0,60,
=0,60,  =88,4,
=88,4, 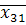 =8,72
=8,72
II гр. 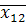 =1,39,
=1,39, 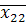 =87,3,
=87,3, 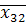 =5,53.
=5,53.
Дискриминантная функция f(x)в данном случае имеет вид:
f (х) = 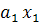 +
+ 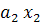 +
+  (18)
(18)
Коэффициенты 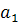 ,
, 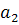 и
и  вычисляются по формуле:
вычисляются по формуле:
A= 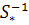 (
( -
- 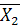 ), (19)
), (19)
где  и
и 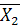 - векторы средних в первой и второй группах; А - вектор коэффициентов;
- векторы средних в первой и второй группах; А - вектор коэффициентов; 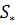 - матрица, обратная совместной ковариационной матрице.
- матрица, обратная совместной ковариационной матрице.
Для определения совместной ковариационной матрицы  нужно рассчитать матрицы
нужно рассчитать матрицы 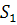 и
и  . Каждый элемент этих матриц представляет собой разность между соответствующим значением исходной переменной
. Каждый элемент этих матриц представляет собой разность между соответствующим значением исходной переменной 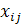 и средним значением этой переменной в данной группе
и средним значением этой переменной в данной группе 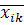 (k - номер группы):
(k - номер группы):
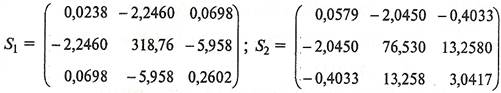
Тогда совместная ковариационная матрица 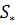 будет равна:
будет равна:
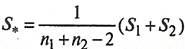 , (20)
, (20)
где  ,
, 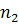 - число объектов l-й и 2-й группы;
- число объектов l-й и 2-й группы;
 (21)
(21)
Обратная матрица 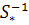 будет равна:
будет равна:
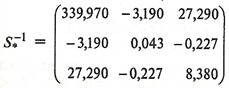 .(22)
.(22)
Отcюда находим вектор коэффициентов дискриминантной функции по формуле:
 (23)
(23)
т.е. 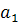 =-185,03,
=-185,03, 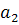 =1,84,
=1,84,  =4,92.
=4,92.
Подставим полученные значения коэффициентов в формулу (18) и рассчитаем значения дискриминантной функции для каждого объекта:
 (24)
(24)
Тогда константа дискриминации С будет равна:
С =  (94,4238-70,0138) = 12,205.
(94,4238-70,0138) = 12,205.
После получения константы дискриминации можно проверить правильность распределения объектов в уже существующих двух классах, а также провести классификацию новых объектов.
Рассмотрим, например, объекты с номерами 1, 2, З, 4. Для того чтобы отнести эти объекты к одному из двух множеств, рассчитаем для них значения дискриминантных функций (по трем переменным):
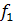 = -185,03 х 1,07 + 1,84 х 93,5 + 4,92 х 5,30 = 0,1339,
= -185,03 х 1,07 + 1,84 х 93,5 + 4,92 х 5,30 = 0,1339,
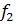 = -185,03 х 0,99 + 1,84 х 84,0 + 4,92 х 4,85 = -4,7577,
= -185,03 х 0,99 + 1,84 х 84,0 + 4,92 х 4,85 = -4,7577,
 = -185,03 х 0,70 + 1,84 х 76,8 + 4,92 х 3,50 = 29,0110,
= -185,03 х 0,70 + 1,84 х 76,8 + 4,92 х 3,50 = 29,0110,
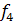 = -185,03 х 1,24 + 1,84 х 88,0 + 4,92 х 4,95 = -43,1632.
= -185,03 х 1,24 + 1,84 х 88,0 + 4,92 х 4,95 = -43,1632.
Таким образом, объекты 1, 2 и 4 относятся ко второму классу, а объект 3 относится к первому классу, так как 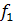 < с,
< с, 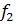 < с,
< с,  > с,
> с, 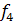 < с.
< с.
|
|
|
4. Классификация при наличии k обучающих выборок
При необходимости можно проводить разбиение множества объектов на k классов (при k > 2). В этом случае нужно рассчитать k дискриминантных функций, так как классы будут отделяться друг от друга индивидуальными разделяющими поверхностями. На рис. 3 показан случай с тремя множествами и тремя дискриминантными переменными:
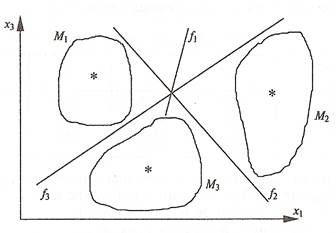
Рис.3 Три класса объектов и разделяющие их прямые
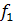 – первая,
– первая, 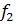 – вторая,
– вторая,  - третья дискриминантные функции.
- третья дискриминантные функции.
Пример 2. Рассмотрим случай, когда существует три класса (множества) объектов. Для этого к двум классам из предыдущего примера добавим еще один. В этом случае будем иметь уже три матрицы исходных данных:
 (25)
(25)
Если в процессе дискриминации используются все четыре переменные (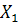 ,
,  ,
, 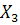 ,
, 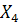 ) то для каждого класса дискриминантные функции имеют вид:
) то для каждого класса дискриминантные функции имеют вид:
 (26)
(26)
Определим теперь, к какому классу можно отнести каждое из четырех наблюдений, приведенных в табл.2:
Таблица 2- Исходные данные
| Номер наблюдения |
|
|
|
|
| 1 | 1,07 | 93,5 | 5,30 | 5385 |
| 2 | 0,99 | 84,0 | 4,85 | 5225 |
| 3 | 0,70 | 76,8 | 3,50 | 5190 |
| 4 | 1,24 | 88,0 | 4,95 | 6280 |
Подставим соответствующие значения переменных 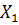 ,
,  ,
,  ,
, 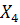 в выражение (26) и вычислим затем разности:
в выражение (26) и вычислим затем разности:
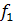 -
- 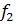 =-20792,082+31856,41=11064,328
=-20792,082+31856,41=11064,328 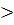 0,
0,
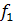 -
-  =-20792,082+40016,428=19224,346
=-20792,082+40016,428=19224,346 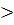 0.
0.
Следовательно, наблюдение 1 в табл.2 относится к первому классу. Аналогичные расчеты показывают, что и остальные три наблюдения следует отнести тоже к первому классу.
Чтобы показать влияние числа дискриминантных переменных на результаты классификации, изменим условие последнего примера. Будем использовать для расчета дискриминантных функций только три переменные: 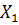 ,
, 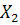 ,
, 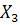 . В этом случае выражения для дискриминантныx функций будут иметь вид:
. В этом случае выражения для дискриминантныx функций будут иметь вид:
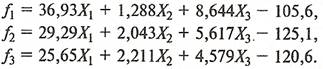 (27)
(27)
Подставив в эти выражения значения исходных переменных для классифицируемых объектов, нетрудно убедиться, что все они попадают в третий класс, так как
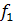 -
- 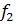 =-26,87
=-26,87  0,
0,
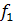 -
-  =-37,68
=-37,68 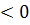 ,
,
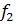 -
-  =-10,809
=-10,809 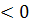 .
.
Таким образом, мы видим, что изменение числа переменныx сильно влияет на результат дискриминантного анализа. Чтобы судить о целесообразности включения (удаления) дискриминантной переменной, обычно используют специальные статистические критерии, позволяющие оценить значимость ухудшения или улучшения разбиения после включения (удаления) каждой из отобранных переменных.
|
|
|
|
|
|