 |
Пример № 2. Рис. 8. Теплопередача через цилиндрическую стенку.
|
|
|
|
Пример № 2
По стальной трубе с наружным диаметром d2 = 162 мм и толщиной стенки  = 6 мм движется газ со средней температурой tг = 820°С (коэффициент теплопроводности материала стенки трубы –
= 6 мм движется газ со средней температурой tг = 820°С (коэффициент теплопроводности материала стенки трубы – 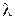 = 40 Вт/(м∙ К)) (рис. 8). Наружная поверхность трубы омывается жидкостью со средней температурой tж = 115°С.
= 40 Вт/(м∙ К)) (рис. 8). Наружная поверхность трубы омывается жидкостью со средней температурой tж = 115°С.
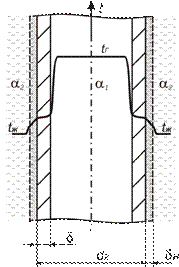
Рис. 8. Теплопередача через цилиндрическую стенку.
Коэффициент теплоотдачи от газа к внутренней поверхности трубы равен 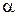 1 = 39 Вт/(м2∙ К), а от внешней поверхности к жидкости –
1 = 39 Вт/(м2∙ К), а от внешней поверхности к жидкости – 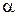 2 = 1985 Вт/(м2∙ К).
2 = 1985 Вт/(м2∙ К).
Определить линейную плотность теплового потока qℓ и температуры внутренней и внешней поверхности трубы tс1 и tс2.
Как численно изменяется линейная плотность теплового потока и температуры внутренней и внешней поверхности трубы, если с внешней стороны труба покрылась слоем загрязнения или накипи толщиной  н = 1, 7 мм с коэффициентом теплопроводности
н = 1, 7 мм с коэффициентом теплопроводности 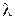 н = 0, 8 Вт/(м∙ К) при условии, что коэффициент теплоотдачи
н = 0, 8 Вт/(м∙ К) при условии, что коэффициент теплоотдачи 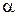 2 не изменяется.
2 не изменяется.
Решение.
Для начала определим линейную плотность теплового потока без накипи по формуле (6):
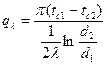 ,
,
где в нашем случае tc1 и tc2 неизвестны. Найдем их используя преобразования в рассмотренном выше примере (см. пример 1).
Согласно формуле (2) плотность теплового потока
q = a× (tж – tc ).
Для внутренней стенки цилиндра данная формула примет вид:
q = a1× (tг – tc1 ).
Выразим отсюда tc1:
 . (*)
. (*)
Аналогично для внешней стенки цилиндра:
q = a2× (tж – tc2 ).
Выразим отсюда tc2:
 . (**)
. (**)
При этом, используя формулу (5), для однослойной стенки плотность теплового потока составит:
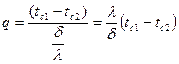 .
.
В полученное выражение вместо tc1 и tc2 подставим выражения из (*) и (**):
 .
.
Вынесем  и
и  в правой части уравнения за скобки и перенесем в влево:
в правой части уравнения за скобки и перенесем в влево:
|
|
|
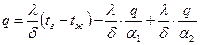 ;
;
 .
.
Левую часть сгруппируем по q и выразим плотность теплового потока:
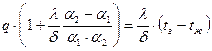 ;
;
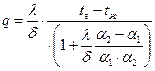 . (***)
. (***)
В нашем случае λ = 40 Вт/(м∙ К); δ = 6 мм = 0, 006 м; tг = 820°С; tж = 115°С; α 1 = 39 Вт/(м2∙ К); α 2 = 1985 Вт/(м2∙ К).
Тогда 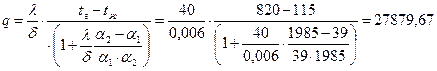 Вт/м2.
Вт/м2.
Зная q можем найти tc1 и tc2 по формулам (*) и (**) соответственно:
 °С ≈ 105°С;
°С ≈ 105°С;
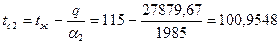 °С ≈ 101°С.
°С ≈ 101°С.
Кроме того, d1 = d2 – δ = 162 – 6 = 156 мм = 0, 156 м.
Тогда 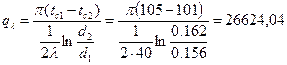 Вт/м.
Вт/м.
Теперь определим, как численно изменяется линейная плотность теплового потока и температуры внутренней и внешней поверхности трубы, если с внешней стороны труба покрылась слоем загрязнения или накипи толщиной  н = 1, 7 мм с коэффициентом теплопроводности
н = 1, 7 мм с коэффициентом теплопроводности 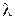 н = 0, 8 Вт/(м∙ К) при условии, что коэффициент теплоотдачи
н = 0, 8 Вт/(м∙ К) при условии, что коэффициент теплоотдачи 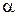 2 не изменяется.
2 не изменяется.
Для этого представим tc1 и tc3 по формулам (*) и (**) соответственно:
 ;
;
 .
.
По формуле (5) для многослойной стенки найдем q:
 ;
;
При помощи преобразований выразим q через остальные переменные:
 ;
;
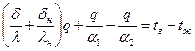 ;
;
 ;
;
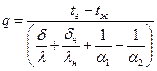 ;
;
В нашем случае
 Вт/м2.
Вт/м2.
Найдем tc1 и tc3 по формулам (*) и (**) соответственно:
 °С ≈ 161°С;
°С ≈ 161°С;
 °С ≈ 102°С.
°С ≈ 102°С.
Кроме того, d1 = d2 – δ = 162 – 6 = 156 мм = 0, 156 м; d3 = d2 + δ н = 162 + 1, 7 = 163, 7 мм = 0, 1637 м.
Тогда  Вт/м.
Вт/м.
Вывод: если с внешней стороны труба покрылась слоем накипи, то температура внутренней стенки повысится 56°С, температура внешней стенки почти не изменится (было 101°С, стало 102°С), а линейный тепловой поток уменьшится 144, 04 Вт/м2.
Пример № 6
По «горячему» надземному трубопроводу с наружным диаметром d2 и толщиной стенки  1 перекачивается нефтепродукт с массовым расходом G (рис. 4).
1 перекачивается нефтепродукт с массовым расходом G (рис. 4).
Температура нефтепродукта после тепловой станции tж1, а в конце участка перед следующей тепловой станцией tж2. Температура окружающего воздуха равна tв.
Для уменьшения тепловых потерь трубопровод можно покрыть слоем тепловой изоляции с коэффициентом теплопроводности 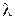 и .
и .
Коэффициент теплопроводности стенки трубы равен 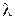 1 = 38 Вт/(м. К). Коэффициент теплоотдачи от наружной поверхности трубопровода к окружающему воздуху считать постоянным и равным
1 = 38 Вт/(м. К). Коэффициент теплоотдачи от наружной поверхности трубопровода к окружающему воздуху считать постоянным и равным 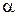 2.
2.
|
|
|
Определить тепловой поток Q через цилиндрическую стенку, если толщина слоя изоляции δ и = 5 мм. Расстояние между тепловыми станциями составляет L. В расчетах принять et ≈ 1.
Как численно изменится расстояние между тепловыми станциями, если изоляцию не применять?
Исходные данные приведены в таблицах 17, 18.

Рис. 4. Схема надземного трубопровода
Исходные данные к примеру № 6
Таблица 17
| Первая цифра номера варианта | Материал тепловой изоляции | 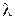 и , Вт/(м. К). и , Вт/(м. К).
| tв. , 0С | 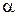 2, Вт/(м2. К). 2, Вт/(м2. К).
|
| пенополиуретан | 0, 04 | -30 |
Таблица 18
| Вторая цифра номера варианта | d2 , мм |  1 ,
мм 1 ,
мм
| Нефте-продукт | G. 10 –6, кг/ч | tж1 , 0С | tж2 , 0С | L , км |
| 12, 5 | Нефть III | 1, 8 |
Решение.
Тепловой поток Q определим по формуле (4):
Q = ql l,
где 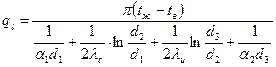 ,
,
l – длина трубопровода (в нашем случае l = L = 210 км).
За температуру жидкости tж примем среднюю арифметическую температур на входе в рассматриваемый участок и на выходе из него; она будет также определяющей температурой при вычислении свойств жидкости:
 °С
°С
Найдем внутренний диаметр трубопровода:
d1 = d2 - 2∙ δ 1 = 820 - 2∙ 12, 5 = 795 мм = 0, 795 м.
Найдем диаметр трубопровода с изоляцией:
d3 = d2 + 2∙ δ и = 820 - 2∙ 5 = 830 мм = 0, 83 м.
Для определения теплового потока Q необходимо знать коэффициент теплоотдачи нефтепродукта к внутренней стенке трубопровода α 1.
Вначале необходимо установить режим течения. Для этого найдем скорость движения и далее число Рейнольдса (Re).
Зная расход жидкости и параметры трубы, определим скорость жидкости
 .
.
Выразим ω:
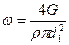 . (*)
. (*)
Плотность нефтепродукта найдем по формуле (9) приложения:
 = S4 – S5 t, кг/м3 (9)
= S4 – S5 t, кг/м3 (9)
Из таблицы 3 приложения коэффициенты S4 и S5 для нефтепродукта Нефть III для температурного диапазона 30-90°С (т. к. tж = 52, 5°С) равны:
S4 = 860; S5 = 0, 717.
Тогда ρ = 860 – 0, 717 ∙ 52, 5 ≈ 822, 4 кг/м3.
По условию задачи G∙ 10-6 = 1, 8 кг/ч (см. таблицу 18 условия задачи). Тогда G = 1, 8∙ 106 кг/ч = 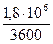
 = 500 кг/с. Подставим в формулу (*) данного примера и найдем ω:
= 500 кг/с. Подставим в формулу (*) данного примера и найдем ω:
 м/с.
м/с.
Определим число Рейнольдса:
|
|
|
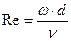 , (**)
, (**)
где d = d1 – внутренний диаметр трубы, υ – кинематическая вязкость жидкости.
Для нефтепродукта Нефть III кинематическую вязкость определим по формуле (10а) приложения
 ∙ 106 = exp [exp (A1 - A2 lnT)] – 0, 6, м2/с.
∙ 106 = exp [exp (A1 - A2 lnT)] – 0, 6, м2/с.
Из таблицы 3 приложения для температурного диапазона 30-90°С (т. к. tж = 52, 5°С) имеем:
A1 = 26, 21; A2 = 4, 3392; Т = tж + 273 = 52, 5+273 = 325, 5 К.
Тогда
 19, 94699 м2/с.
19, 94699 м2/с.
Отсюда  м2/с.
м2/с.
Подставим в формулу (**) данного примера и найдем коэффициент Рейнольдса:
 .
.
Из таблицы 1 раздела «Основные расчетные соотношения» для случая вынужденного течения жидкости в трубе при Re = 4, 8823∙ 104 > 10000 определим коэффициента Нуссельта по уравнению подобия
Nu = 0, 021 Re0, 8× Pr0, 43 × et ,
где et =  ;
;
 – число Прандтля (для жидкости);
– число Прандтля (для жидкости);
Prc – число Прандтля для стенки трубопровода.
Мы уже определили ρ = 822, 4 кг/м3 и υ = 19, 94699∙ 10-6 м2/с.
По формуле (8) приложения определим ср:
Cp = S2 + S3 t, Дж/(кг∙ К).
Из таблицы 3 приложения S2 = 1707; S3 = 6, 45; t = tж = 52, 5°С.
По формуле (7) приложения определим λ ж:
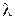 = S0 – S1 t, Вт/(м∙ К).
= S0 – S1 t, Вт/(м∙ К).
Из таблицы 3 приложения S0 = 0, 154; S1∙ 104 = 1, 06 => S1∙ = 1, 06∙ 10-4; t = = tж = 52, 5°С.
Тогда λ ж = λ = 0, 154 – 1, 06∙ 10-4 ∙ 52, 5 ≈ 0, 1484 Вт/(м∙ К)
Тогда ср = 1707+6, 45 ∙ 52, 5 = 2045, 625 Дж/(кг∙ К).
Найдем  .
.
Тогда
Nu = 0, 021 Re0, 8× Pr0, 43 × et = 0, 021∙ (4, 8823∙ 104)0, 8∙ 0, 274960, 43∙ 1 = 67, 92111.
По формуле (7) из раздела «Основные расчетные соотношения»
Nu = 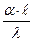 ,
,
где 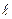 – линейный размер (в нашем случае
– линейный размер (в нашем случае 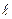 = d1);
= d1);
α – коэффициент теплоотдачи, Вт/(м2∙ К);
λ = λ ж.
Из данной формулы следует, что
 Вт/(м2∙ К).
Вт/(м2∙ К).
Таким образом, можем определить тепловой поток Q
Q = ql l,
где l = L = 210 км;
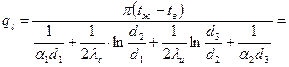
 Вт/м.
Вт/м.
Тогда Q = 853, 4881∙ 210000 = 179232500 ≈ 179 МВт.
Определим, как численно изменится расстояние между тепловыми станциями, если изоляцию не применять:
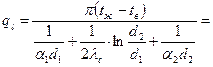
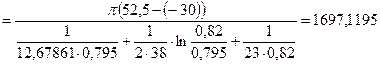 Вт/м.
Вт/м.
Поскольку Q = ql l =>  м, или l ≈ 105, 6 км.
м, или l ≈ 105, 6 км.
Вывод:
1) Q = 179 МВт;
2) расстояние L уменьшится в  раза.
раза.
|
|
|


