 |
I. Основные теоретические положения
|
|
|
|
Тема: Уравнения с разделяющимися переменными
I. Основные теоретические положения
Основные понятия
Определение. Функциональное уравнение вида
, (1.1.)
связывающее независимую переменную 
, искомую функцию 
и ее производную называется дифференциальным уравнением первого порядка.
Формы записи дифференциального уравнения (1.1.):
· 
- нормальная форма (
, т.к. 
)
· 
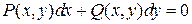- дифференциальная форма
Определение. Решением (частным решением) уравнения (1.1) на интервале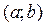 
называется любая функция 
, которая при подстановке вместе со своей производной обращает уравнение в верное равенство относительно всех 
. Уравнение 
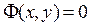, определяющее это решение как неявную функцию, называется интегралом (частным интегралом) дифференциального уравнения.
Определение. Функция 
называется общим решением уравнения (1.1.), если:
1) при любом допустимом значении параметра 
функция является частным решением этого уравнения;
2) любое частное решение уравнения может быть представлено в виде 
при некотором значении 
параметра .
Определение. Уравнение 
, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения первого порядка.
Задачей Коши для дифференциального уравнения (1.1.) называется задача отыскания частного решения , удовлетворяющего заданному начальному условию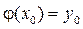 
.
Процесс нахождения решения дифференциального уравнения называется его интегрированием.
Универсального способа нахождения решения дифференциального уравнения (1.1.) не существует, т.к. нет универсального способа проинтегрировать произвольную функцию. Рассмотрим ряд уравнений, для которых разработаны методы интегрирования.
|
|
|
Уравнения с разделяющимися переменными (УРП)
Определение. Дифференциальное уравнение
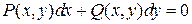
является УРП, если функци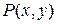и 
и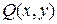 
удовлетворяют условию
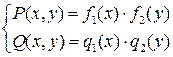, (1.2.)
т.е. коэффициенты перед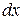 
и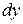 
можно представить в виде произведения двух функций (чисел), одна из которых зависит только от 
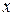, другая – только от 
.
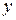Определение. Дифференциальное уравнение
является УРП, если функция 
удовлетворяет условию
, (1.3.)
Метод решения УРП: разделение дифференциалов (переменных)
Суть: в одну часть равенства собираем все, что касается переменной 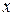, в другую – все, что касается переменной .
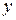II. Решить дифференциальное уравнение
Пример 1: 
Решение:
1. Уравнение дано в дифференциальной форме, поэтому выписываем функции 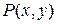(коэффициент перед 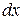) и 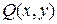(коэффициент перед 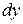) и проверяем для них условие (1.2.):
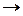УРП
2. Разделяем дифференциалы:
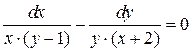
в левую часть равенства собираем по переменной 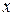(т.к. слева 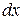), в правую часть собираем по переменной 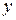(т.к. справа ):
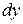интегрируем обе части
- общий интеграл.
Пример 2: 
Решение:
1. Выражаем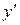 
, чтобы определить тип уравнения, и проверяем для правой части выполнение условия (1.3.):
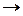УРП
2. Разделяем дифференциалы, предварительно заменив :
в левую часть равенства собираем по переменной 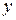(т.к. слева вверху по 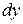), в правую часть собираем по переменной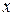
интегрируем обе части
(*)
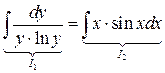3. Находим значения интегралов 
и 
:
4. Найденные значения интегралов подставляем в (*):
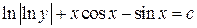- общий интеграл
5. Решаем задачу Коши (находим значение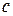 
):
в общий интеграл
в общий интеграл
.
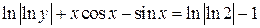№2
Тема: Однородные уравнения и их решение
I. Основные теоретические положения
Определение. Дифференциальное уравнение
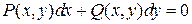
является однородным, если функци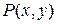и и 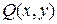удовлетворяют условию
, (2.1.)
т.е. функци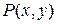и и 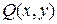являются однородными одинакового порядка 
.
Определение. Дифференциальное уравнение
|
|
|
(2.2.)
так же является однородным, т.е. правая часть представляет собой функцию, зависящую от отношения 
.
Метод решения однородного уравнения: замена переменной
Суть: отношение обозначается за новую переменную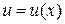 
, в результате чего однородное уравнение сводится к УРП.
Алгоритм решения однородного уравнения:
1. Привести уравнение к виду (2.2.), где .
2. Сделать замену:
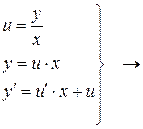в (2.2.) и решить.
3. Вернуться к замене.
|
|
|
