 |
Линейное однородное дифференциальное уравнение с постоянными коэффициентами
|
|
|
|
Определение. Дифференциальное уравнение вида
, (6.1.)
где 
- постоянные коэффициенты (числа), функции 
входят в уравнение в первой степени, не перемножаясь между собой, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами.
Структура общего решения 
однородногоуравнения (6.1.):
,
где 
, 
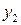образуют ФСР (фундаментальную систему решений).
Определение. Характеристическим уравнением для уравнения (6.1.) называется уравнение вида
(6.2.)
(получается из уравнения (8.1.) заменой производных 
на степени 
)
Пусть 
и 
– корни характеристического уравнения (6.2.). Если:
1) и – действительные и 
ФСР: 
, 
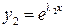
. (6.3.)
2) и – действительные и 
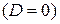
ФСР: , 
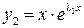
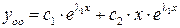. (6.4.)
3) 
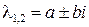– комплексно сопряженные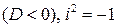 
ФСР: 
, 
. (6.5.)
2. Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами
Определение. Дифференциальное уравнение вида
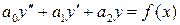, (6.6.)
где - постоянные коэффициенты (числа), 
, функции входят в уравнение в первой степени, не перемножаясь между собой, называется линейным неоднородным дифференциальным уравнением с постоянными коэффициентами.
Структура общего решения 
неоднородного уравнения (6.6.):
,
где 
общее решение соответствующего однородного уравнения;
любое частное решение неоднородного уравнения.
Для нахождения общего решения соответствующего однородного уравнения достаточно составить характеристическое уравнение (6.2.) и использовать формулы (6.3.) – (6.5.).
Для нахождения любого частного решения неоднородного уравнения 
используется метод Лагранжа (общий метод).
Метод Лагранжа: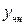 
ищем в таком же виде, что и , только 
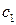и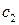 
считаются не числами, а функциями от 
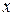, т.е.
,
где от функций 
и 
требуют, чтобы они удовлетворяли условию
|
|
|
(6.7.)
Решаем систему относительно 
и 
:
подставляем в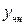 
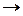записываем 
.
II. Решить дифференциальное уравнение
Пример 1: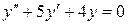 
Решение:
Составляем характеристическое уравнение и находим его корни
, 
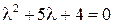
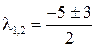
(1 случай, формула (6.3.))
ФСР: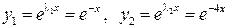 
.
Пример 2: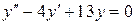 
Решение:
Составляем характеристическое уравнение и находим его корни
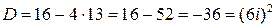
(3 случай, 
, формула (6.5.))
ФСР: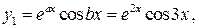 
.
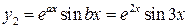
Пример 3: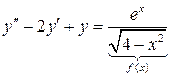 
Задача:
1. 
: 
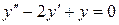
- характеристическое уравнение
(2 случай, формула (6.4.))
ФСР: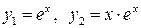 
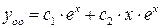
2. : частное решение находим методом Лагранжа
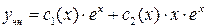
а) Составляем систему (6.7.) и находим и :
(*)
Вычтем из первого уравнения системы (*) второе:
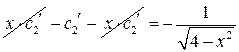
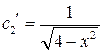
Подставив найденное значение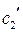 
в первое уравнение системы (*) получим:
.
б) Находим 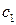и :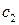
.
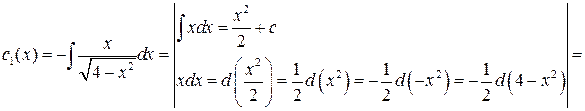
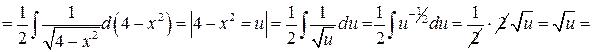
Подставляем и в :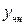
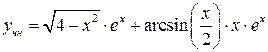
3. Записываем 
:
.
№ 7
Тема: Линейные неоднородные уравнения с постоянными
коэффициентами и правой частью специального вида
(метод неопределенных коэффициентов)
I. Основные теоретические положения
Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами
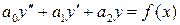
где - постоянные коэффициенты (числа), .
В тех случаях, когда правая часть уравнения 
имеет специальный вид (является квазиполиномом)
,
где 
и 
- многочлены степени 
и 
соответственно,
-характеристическое число квазиполинома,
частное решение неоднородного уравнения удобнее находить методом неопределенных коэффициентов (методом подбора).
Метод неопределенных коэффициентов: 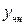ищем в таком же виде, в каком представлена функция , только вместо известных коэффициентов в многочленах будут стоять неопределенные, которые находятся при подстановке в исходное дифференциальное уравнение составленной формулы для 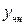(см. таблицу7.1.)
Таблица 7.1.
| Вид правой части | 
| Формула для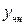
|
1. 
| 
| 
|
2. 
| 
| 
|
3. 
или
| 
| 
|
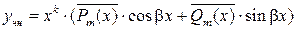
4. 
|
| 
|
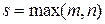
Замечания:
1) если не является корнем характеристического уравнения 
,
|
|
|
если – корень характеристического уравнения (повтор – 
раз) 
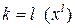
2) Общий вид многочленов с неопределенными коэффициентами:
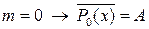
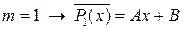
и т.д.
3) если правая часть исходного уравнения имеет вид 
, причем 
и 
относятся к разным случаям из таблицы (9.1.), то 
, где
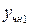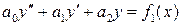- частное решение уравнения
,
- частное решение уравнения
.
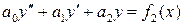Т.к. 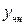- решение, то при подстановке его в исходное уравнение получим тождество, в котором, приравнивая коэффициенты при одинаковых линейно независимых функциях слева и справа получим систему линейных уравнений, решив которую найдем коэффициенты.
|
|
|
