 |
II. Решить дифференциальное уравнение
|
|
|
|
Пример 1: 
Решение:
1. Выражаем 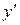 , чтобы определить тип уравнения:
, чтобы определить тип уравнения:
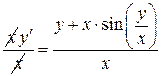
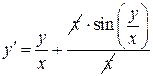
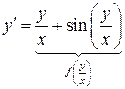
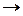 однородное (*)
однородное (*)
(данное уравнение не является УРП, т.к. в правой части нет общих множителей в первом и во втором слагаемом).
2. Делаем замену: 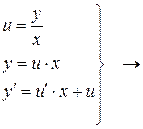 в (*)
в (*)
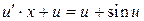
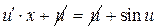

 - УРП
- УРП
заменяем 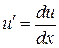 (т.к.
(т.к. 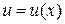 )
)
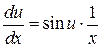
в левую часть равенства собираем по переменной 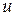 (т.к. слева вверху
(т.к. слева вверху  ), в правую часть собираем по переменной
), в правую часть собираем по переменной 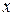
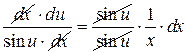
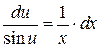
интегрируем обе части

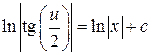
3. Возвращаемся к замене 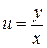 :
:
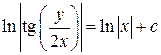 - общий интеграл.
- общий интеграл.
4. Решаем задачу Коши (находим 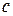 ):
):
 в общий интеграл
в общий интеграл
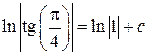
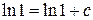
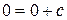
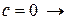 в общий интеграл
в общий интеграл
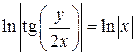 .
.
Пример 2: 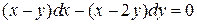
Решение:
1. Уравнение дано в дифференциальной форме, поэтому выписываем функции 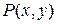 (коэффициент перед
(коэффициент перед 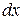 ) и
) и 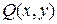 (коэффициент перед
(коэффициент перед 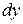 ) и проверяем для них выполнение условия (2.1.):
) и проверяем для них выполнение условия (2.1.):
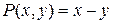
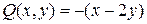
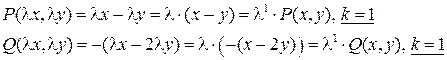
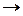 однородное
однородное
2. Приводим уравнение к виду (2.2.):
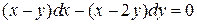
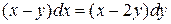
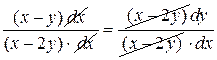
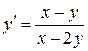
чтобы выделить отношение  в правой части, числитель и знаменатель дроби разделим на
в правой части, числитель и знаменатель дроби разделим на 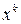 (т.е. на
(т.е. на 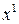 , т.к.
, т.к. 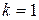 )
)
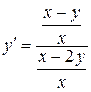
 (*).
(*).
2. Делаем замену:
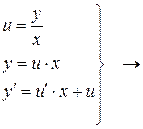 в (*)
в (*)
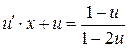

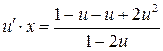
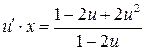
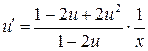 - УРП
- УРП
заменяем 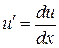 (т.к.
(т.к. 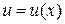 )
)

в левую часть равенства собираем по переменной 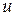 (т.к. слева вверху
(т.к. слева вверху  ), в правую часть собираем по переменной
), в правую часть собираем по переменной 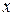
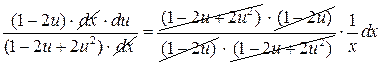
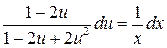
интегрируем обе части
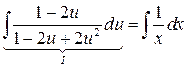
Найдем значение интеграла  :
:

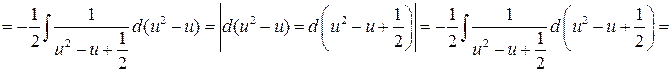
 .
.
Следовательно, общий интеграл имеет вид
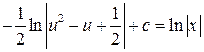 .
.
3. Возвращаемся к замене 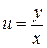 :
:
 .
.
№3
Тема: Линейные уравнения, уравнения Бернулли и их решение
I. Основные теоретические положения
| Общий вид | Название | Подстановка |
1. 
| линейное относительно 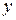
| 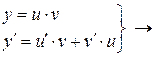 в уравнение в уравнение
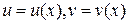
|
2. 

| ур. Бернулли относительно 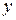
| |
3. 
| линейное относительно 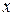
|  в уравнение в уравнение
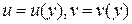
|
4. 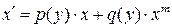

| ур. Бернулли относительно 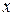
|
Метод решения: метод Бернулли
Суть: общее решение исходного уравнения ищется в виде произведения двух неизвестных функций 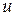 и
и 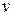 , причем, одна из них (как правило, функция
, причем, одна из них (как правило, функция 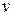 ) содержит произвольную постоянную
) содержит произвольную постоянную 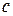 .
.
|
|
|
Замечание: при нахождении функций 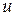 и
и 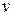 часто используются основные свойства логарифмов:
часто используются основные свойства логарифмов:
1. 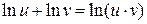
|
2. 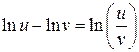
|
3. 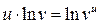
|
4. 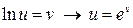
|
II. Решить дифференциальное уравнение
Пример 1: 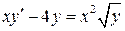
Решение:
1. Выразим 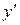 , чтобы определить тип уравнения:
, чтобы определить тип уравнения:
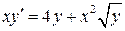

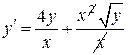
 - Бернулли (
- Бернулли (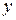 ),
), 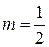
(полученное уравнение не является УРП, т.к. в правой части после вынесения общего множителя в скобке останутся обе переменные, и не является однородным, т.к. второе слагаемое не содержит отношения  ).
).
2. Пусть общее решение уравнения имеет вид (делаем подстановку):

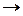 в уравнение
в уравнение
Получим

Перенесем все слагаемые в левую часть равенства:
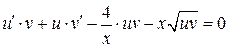
Сгруппируем первое и третье слагаемое:
 (*)
(*)
Согласно методу скобку приравниваем к нулю:
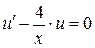
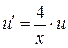 - УРП
Заменяем - УРП
Заменяем 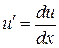 (т.к. (т.к. 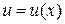 ): ):
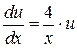
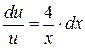

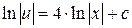 Выражаем функцию
Выражаем функцию 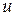 , используя свойства логарифмов: , используя свойства логарифмов:
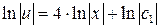

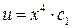 зададим произвольным образом константу
зададим произвольным образом константу 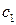 : :
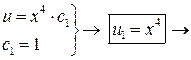 в (*) в (*)
| 
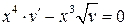
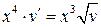
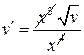
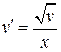 - УРП
Заменяем - УРП
Заменяем 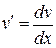 (т.к. (т.к. 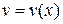 ): ):

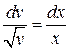

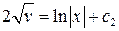 Выражаем функцию
Выражаем функцию 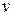 : :
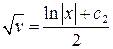
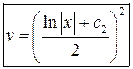
|
3. Записываем общее решение исходного уравнения (возвращаемся к исходной переменной 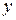 ):
):
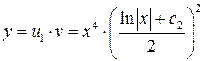 .
.
Пример 2: 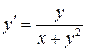
Решение:
1. Перевернем уравнение, чтобы почленно поделить числитель на знаменатель в правой части:
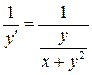
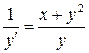
т.к.  , то
, то
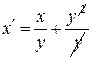
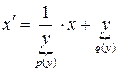 - линейное (
- линейное (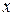 )
)
2. Пусть общее решение уравнения имеет вид (делаем подстановку):

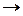 в уравнение
в уравнение
Получим
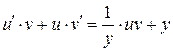
Перенесем все слагаемые в левую часть равенства:
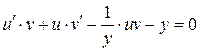
Сгруппируем первое и третье слагаемое:
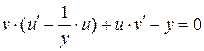 (*)
(*)
Согласно методу скобку приравниваем к нулю:
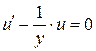
 - УРП
Заменяем - УРП
Заменяем 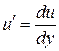 (т.к. (т.к.  ): ):
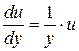

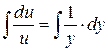
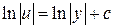 Выражаем функцию
Выражаем функцию 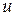 , используя свойства логарифмов: , используя свойства логарифмов:


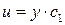 Зададим произвольным образом константу
Зададим произвольным образом константу 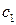 : :
 в (*) в (*)
| 
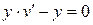
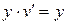
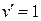 - УРП
Заменяем - УРП
Заменяем 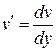 (т.к. (т.к.  ): ):

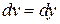
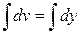
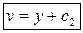
|
3. Записываем общее решение исходного уравнения (возвращаемся к исходной переменной 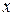 ):
):
 .
.
№4
Тема: Уравнения в полных дифференциалах
I. Основные теоретические положения
Определение. Дифференциальное уравнение
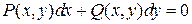
называется уравнением в полных дифференциалах (УПД), если функции 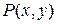 и
и 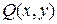 удовлетворяют тождеству
удовлетворяют тождеству
|
|
|
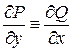 , (4.1.)
, (4.1.)
т.е. левая часть уравнения есть полный дифференциал некоторой функции  .
.
В этом случае исходное уравнение можно записать в виде
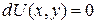 ,
,
общий интеграл которого имеет вид

Задача: найти функцию  .
.
Алгоритм решения УПД:
1. Из исходного уравнения выписать функции 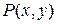 и
и 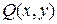 ;
;
2. Проверить выполнение условия (4.1.):
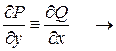 УПД
УПД
3. Составить систему и решить ее:
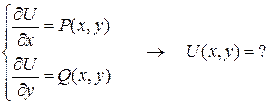 (4.2.)
(4.2.)
4. Записать общий интеграл исходного уравнения:

|
|
|


