 |
II. Вычислить неопределённый интеграл
|
|
|
|
I. Основные теоретические положения
Основные понятия
Определение. Функция 
называется первообразной для функции 
на некотором промежутке изменения аргумента, если в каждой точке этого промежутка выполняется равенство
Определение. Неопределённым интегралом от функции называется совокупность всех первообразных этой функции на заданном промежутке.
Обозначени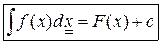е: 
, где
– подынтегральная функция;
– подынтегральное выражение;
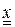– переменная интегрирования;
– произвольная постоянная.
Определение. Операция нахождения неопределённого интеграла от некоторой функции называется интегрированием этой функции.
Свойства неопределённого интеграла:
10. 
! 
(почленное деление числителя на знаменатель)
! 
20. 
, где 
30. 
(интегрирование и дифференцирование – это взаимно
обратные операции).
Таблица основных интегралов (ТОИ)
1. 
, 
, 
, 
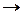
2. 
3. 
4. 
5. 
6. 
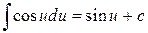
7. 
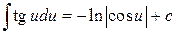
8. 
9. 
10. 
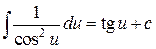
11. 
12. 
13. 
14. 
15. 
16. 
Почти” табличные интегралы и их вычисление
Интегралы вида 
будем называть “почти” табличными, для вычисления которых используются преобразования дифференциала
(1.1.)
(1.2.)
Данные правила легко запомнить:
· если под знаком дифференциала к выражению (переменной) прибавить любое число, то перед дифференциалом коэффициентов не появиться (1.1.);
· если под знаком дифференциала выражение (переменную) умножить на число, то перед дифференциалом появиться коэффициент, обратный к этому числу (1.2.).
К “почти” табличным интегралам можно отнести, к примеру, интегралы
, 
, 
, …
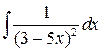II. Вычислить неопределённый интеграл
1. Используя таблицу основных интегралов (ТОИ):
а)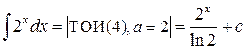 
;
б) 
;
в) 
;
г) 
;
|
|
|
д) 
;
е) 
.
2. Используя ТОИ и свойства неопределённого интеграла (непосредственное интегрирование):
Пример 1: 
раскрываем скобки, применяя свойства степеней, и разбиваем на разность интегралов, вынося постоянный множитель за знак интеграла
.
Пример 2: 
в числителе раскрываем квадрат разности и используем почленное деление числителя на знаменатель, затем разбиваем на сумму и разность интегралов
.
3. Используя преобразования дифференциала:
Пример 3: 
данный интеграл является “почти” табличным (мешает “3”), поэтому используем преобразование дифференциала (1.2.)
.
Пример 4: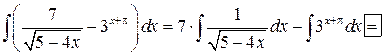 
оба интеграла являются “почти” табличными (в первом мешает “–4” и “5”, во втором интеграле “ 
”), используем преобразования дифференциала
для первого интеграла:
(правила (1.1.) и (1.2.))
для второго интеграла:
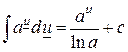
(правило (1.1.))
.
№2
Тема: Подведение (внесение) под знак дифференциала
(введение новой переменной)
I. Основные теоретические положения
или 
Если под знаком интеграла стоит произведение нескольких функций и интеграл от одного из множителей – табличный, то для вычисления интеграла применяется подведение (внесение) под знак дифференциала:
| (2.1.) |
Суть: формула (2.1.) “избавляет” от одного из множителей под знаком интеграла, а интеграл от оставшегося множителя сводится к табличному или к “почти” табличному интегралу после введения новой переменной.
Необходимо помнить:
1. вносим ту функцию под знак дифференциала, интеграл от которой –
табличный;
2. при вычислении интеграла в правой части формулы (2.1.) “ 
” не
пишется.
II. Вычислить неопределённый интеграл
Пример 1: 
представим дробь в виде произведения двух множителей и выделим тот, интеграл от которого – табличный, его вносим под знак дифференциала
разбиваем на разность интегралов, причем, интеграл от первого слагаемого – “почти” табличный, поэтому для его вычисления используем преобразование дифференциала (правило (1.1.))
|
|
|
.
Пример 2: 
под знаком интеграла стоит произведение двух множителей, причем интеграл от первого множителя – табличный, его и вносим под знак дифференциала
полученный интеграл является “почти” табличным, поэтому используем преобразование дифференциала (правила (1.1.) и (1.2.))
.
Пример 3: 
представим дробь в виде произведения множителей и выделим тот, интеграл от которого – табличный, вносим под знак дифференциала тот множитель, интеграл от которого более простой
в полученном интеграле стоит произведение, причем, интеграл от первого множителя – табличный, вносим его под знак дифференциала
.
№3
Тема: Интегрирование по частям
|
|
|
