III. Для самостоятельной работы

1.
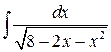
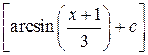
2.
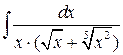
3.
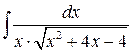
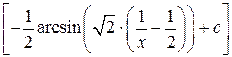
4.
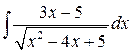
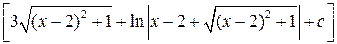
5.

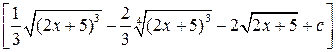
№ 6

Ø Определенный интеграл

Пусть на промежутке [ a; b ] задана функция f (x). Будем считать функцию непрерывной, хотя это не обязательно. Выберем на промежутке [ a; b ] произвольные числа x ₁, x ₂, x ₃, ¼, x_{n -1}, удовлетворяющие условию:
a < x ₁,< x ₂<¼< x_{n -1},< b. Эти числа разбивают промежуток [ a; b ] на n более мелких промежутков: [ a; x ₁], [ x ₁; x ₂], ¼, [ x_{n -1}; b ]. На каждом из этих промежутков выберем произвольно по одной точке: c ₁Î[ a; x ₁], c ₂Î[ x ₁; x ₂], ¼, c_n Î[ x_{n -1}; b ].

Введем обозначения:D x ₁ = x ₁ – a; D x ₂ = x ₂ – x ₁; ¼, D x_n = b – x_{n- 1}.

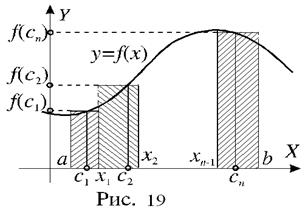Составим сумму: .

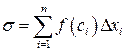Она называется интегральной суммой функции f (x) по промежутку [ a; b ]. Очевидно, что интегральная сумма зависит от способа разбиения промежутка и от выбора точек c_i.

Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рисунке.

Введем обозначение: l = max(D x_i), i = 1, 2, ¼, n.. Величину l иногда называют параметром разбиения.

Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина l стремится к нулю. Определенным интегралом

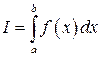
от функции по промежутку [ a; b ] называется предел, к которому стремится интегральная сумма при этом процессе, если предел существует:

.

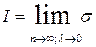Если такой предел существует, то он не зависит от первоначального разбиения промежутка [ a; b ] и выбора точек c_i.

Рис.

Число a называется нижним пределом интегрирования, а число b ¾ верхним пределом интегрирования.

Рассмотрим фигуру, ограни­ченную графиком непрерывной, неотрицательной на промежутке [ a; b ] функции f (x), отрезком [ a; b ] оси X, и прямыми x = a; x = b. Такую фигуру называют криволинейной трапецией. На рисунке криволинейная трапеция выделена штриховкой. Площадь S этой трапеции определяется формулой

Рис.

.

Если f (x) < 0 во всех точках промежутка [ a; b ] и непрерывна на этом промежутке (например, как изображено на рисунке), то площадь криволинейной трапеции, ограниченной отрезком [ a; b ] горизонтальной оси координат, прямыми x = a; x = b и графиком функции y = f (x), определяется формулой

.

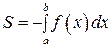Перечислим свойства определенного интеграла:

1) 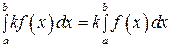(здесь k ‑ произвольное число);

2) ;

3) ;

4) Если cÎ [ a; b ], то .

Из этих свойств следует, например, что .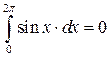

Все приведенные выше свойства непосредственно следуют из определения определенного интеграла.

Рис. 22

Оказывается, что формула из пункта 4 справедлива и тогда, когда cÏ [ a; b ]. Пусть, например, c>b, как изображено на рисунке. В этом случае верны равенства

.

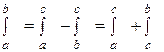Ø Определенный интеграл как функция верхнего предела

Пусть функция f (t) определена и непрерывна на некотором промежутке, содержащем точку a. Тогда каждому числу x из этого промежутка можно поставить в соответствие число

,

Рис.

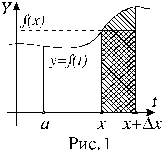
определив тем самым на промежутке функцию I (x), которая называется определенным интегралом с переменным верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x. Для этого сначала рассмотрим приращение функции в точке x при приращении аргумента D x:

D I (x) = I (x + D x) – I (x) =

.

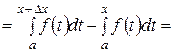
Как показано на рисунке, величина последнего интеграла в формуле для приращения D I (x) равна площади криволинейной трапеции, отмеченной штриховкой. При малых величинах D x (здесь, так же как и везде в этом курсе, говоря о малых величинах приращений аргумента или функции, имеем в виду абсолютные величины приращений, так как сами приращения могут быть и положительными и отрицательными) эта площадь оказывается приблизительно равной площади прямоугольника, отмеченного на рисунке двойной штриховкой. Площадь прямоугольника определяется формулой f (x)D x. Отсюда получаем соотношение

.

В последнем приближенном равенстве точность приближения тем выше, чем меньше величина D x.

Из сказанного следует формула для производной функции I (x):

.

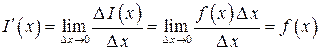Производная определенного интеграла по верхнему пределу в точке x равна значению подынтегральной функции в точке x. Отсюда следует, что функция 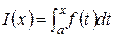является первообразной для функции f (x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде

. (*)

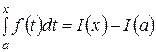Пусть F (x) тоже является первообразной для функции f (x), тогда по теореме об общем виде всех первообразных функции I (x) = F (x) + C, где C — некоторое число. При этом правая часть формулы (*) принимает вид

I (x) – I (a) = F (x) + C – (F (a) + C) = F (x) – F (a). (**)

Из формул (*) и (**) после замены x на b следует формула для вычисления определенного интеграла от функции f (t) по промежутку [ a; b ]:

,

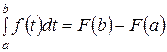которая называется формулой Ньютона-Лейбница. Здесь F (x) — любая первообразная функции f (x).

Для того, чтобы вычислить определенный интеграл от функции f (x) по промежутку [ a; b ], нужно найти какую-либо первообразную F (x) функции f (x) и подсчитать разность значений первообразной в точках b и a. Разность этих значений первообразной принято обозначать символом .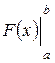

Приведем примеры вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.

Примеры. 1. .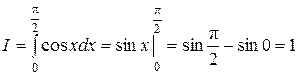

2. .

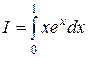Сначала вычислим неопределенный интеграл от функции f (x) = xe^x. Используя метод интегрирования по частям, получаем: . В качестве первообразной функции f (x) выберем функцию e^x (x –1) и применим формулу Ньютона-Лейбница:

I = e^x (x 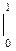–1) =1.

При вычислении определенных интегралов можно применять формулу замены переменной в определенном интеграле:

.

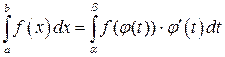Здесь a и b определяются, соответственно, из уравнений j (a) = a; j (b) = b, а функции f, j, j¢ должны быть непрерывны на соответствующих промежутках.

Пример: .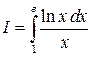

Сделаем замену: ln x = t или x = e^t, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим:

 

.

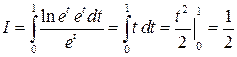При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.

Ø Несобственные интегралы с бесконечными пределами

Если положить промежуток интегрирования бесконечным, то приведенное выше определение определенного интеграла теряет смысл, например, потому что невозможно осуществить условия n ®¥; l®0 для бесконечного промежутка. Для такого интеграла требуется специальное определение.

Пусть функция y = f (x) определена и непрерывна на полубесконечном промежутке [ a;¥), тогда несобственным интегралом с бесконечным пределом называется 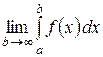, если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.

Аналогично

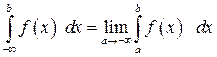и .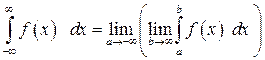

Примеры: 1. 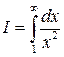. Очевидно: , откуда следует

.

2. ; этот предел не существует, следовательно, не существует или расходится интеграл I.

3. 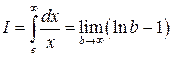; здесь предел также не существует, и интеграл расходится.

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: