 |
Интегрирование рациональных дробей
|
|
|
|
Если исходная рациональная дробь не относится к простейшим, то ее интегрирование проводится по следующему алгоритму.
Алгоритм:
Дано: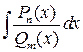 
1) Установить, является ли дробь правильной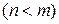 
. Если дробь неправильная 
, то числитель разделить на знаменатель уголком
;
2) Знаменатель правильной дроби разложить на множители;
3) Представить правильную дробь с разложенным знаменателем в виде суммы простейших дробей с неопределёнными коэффициентами. При этом вид разложения определить познаменателю
1 случай: 
2 случай: 
, 
3 случай: 
, 
4) Найти неопределённые коэффициенты:
а) обе части полученного разложения (см. пункт 3)) умножить на знаменатель дроби в левой части, получим равенство (*);
б) выбрать метод нахождения неопределённых коэффициентов
· метод частных значений 
Условие применения: число корней знаменателя дроби (см. пункт 2)) равно числу неопределённых коэффициентов.
Суть:в равенство (*) поочередно подставляем корни из пункта 2).
· метод сравнивания коэффициентов
Условие применения: знаменатель дроби действительных корней не имеет. Суть:в равенстве (*) раскрываем все скобки и приравниваем коэффициенты при одинаковых степенях в слева и справа, решить полученную систему уравнений.
· комбинированный метод
Условие применения: число корней знаменателя дроби (см. пункт 2)) меньше числа неопределённых коэффициентов.
Суть:применяется сначала метод частных значений , затем метод сравнивания коэффициентов.
в) найденные коэффициенты поставить в разложение п.3).
5) Вычислить интеграл от целой части (см. пункт 1)) и простейших рациональных дробей с найденными коэффициентами (см. пункт 4)).
II. Вычислить неопределённые интегралы
|
|
|
Пример 1: 
дробь под знаком интеграла относиться к простейшим дробям второго типа, используем преобразование дифференциала
.
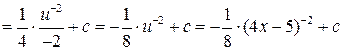Пример 2: 
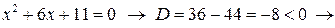простейшая дробь третьего типа,
действуем по указанному в таблице (4.1.) алгоритму
в первом интеграле внесем числитель под знак дифференциала, затем используем правило (1.1.); второй интеграл является табличным
.
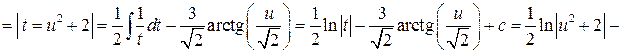
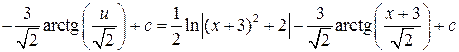Пример 3: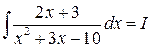 
Легко убедиться, что дискриминант знаменателя положителен, а значит, данная дробь не является простейшей третьего типа, следовательно, действуем по общему алгоритму
1. Степень числителя – 1, степень знаменателя – 2,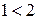 
дробь правильная
2. Разложим знаменатель на множители:
, 
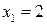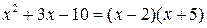
3. Представим дробь с разложенным знаменателем в виде суммы простейших дробей с неопределёнными коэффициентами
4. Домножим разложение (см. пункт 3.) на знаменатель дроби в левой части
(*)
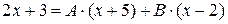число неопределенных коэффициентов равно числу корней знаменателя дроби (см. пункт 2) 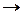метод частных значений
Имеем 
5. Вычисляем интеграл от простейших дробей с найденными коэффициентами
.
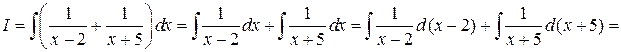
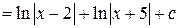Пример 4: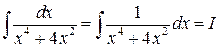 
дробь не относится к простейшим, действуем по общему алгоритму
1. Степень числителя – 0, степень знаменателя – 4, 
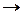дробь правильная
2. Разложим знаменатель на множите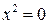ли:
или 
3. Представим дробь с разложенным знаменателем в виде суммы простейших дробей с неопределёнными коэффициентами
4. Домножим разложение (см. пункт 3.) на знаменатель дроби в левой части
(*)
число корней знаменателя дроби (см. пункт 2)) меньше числа неопределённых коэффициентов 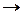комбинированный метод
в равенстве (*) раскрываем все скобки и приравниваем коэффициенты при одинаковых степенях слева и справа
Имеем 
5. Вычисляем интеграл от простейших дробей с найденными коэффициентами
|
|
|
.
III. Для самостоятельной работы
1. 
| 
|
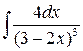
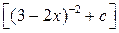
2. 
| 
|
3. 
| 
|
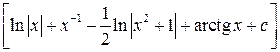
4. 
| 
|
№ 5
Тема: Интегрирование иррациональных выражений
I. Основные теоретические положения
Таблица (5.1.)
| Тип интеграла | Метод вычисления |
1. 
| Подстановка:  , 
|
2. 
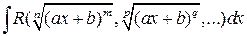
| Подстановка:  , 
|
3. 
| а) выделить полный квадрат в подкоренном
выражении;
б)  выражение под знаком квадрата;
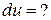в) если интеграл не табличный, то почленное
деление числителя на знаменатель.
|
4. 
| а) подстановка: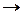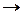   
б) упростить и смотреть пункт 3.
|
|
|
|
