 |
Волновая функция и ее физический смысл
|
|
|
|
Дифракционная картина, наблюдающаяся для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц в различных направлениях - имеются минимумы и максимумы в других направлениях. Наличие максимумов в дифракционной картине означает, что в этих направлениях распределяются волны де Бройля с наибольшей интенсивностью. А интенсивность будет максимальной, если в этом направлении распространяется максимальное число частиц. Т.е. дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности в распределении частиц: где интенсивность волны де Бройля максимальная, там и частиц больше.
Волны де Бройля в квантовой механике рассматриваются как волнывероятности, т.е. вероятность обнаружить частицу в различных точках пространства меняется по волновому закону (т.е. ~ е - iωt ). Но для некоторых точек пространства такая вероятность будет отрицательной (т.е. частица не попадает в эту область). М. Борн (немецкий физик) предположил, что по волновому закону меняется не сама вероятность, а амплитуда вероятности, которую также называют волновой функцией или y-функцией (пси - функцией).
Волновая функция - функция координат и времени.
Квадрат модуля пси-функции определяет вероятность того, что частицабудет обнаружена в пределах объема dV - физический смысл имеет не сама пси-функция, а квадрат ее модуля.
Ψ* - функция комплексно сопряженная с Ψ
(z = a + ib, z* =a- ib, z* - комплексно сопряженное)
Если частица находится в конечном объеме V, то возможность обнаружить ее в этом объеме равна 1, (достоверное событие)
Р = 1 Þ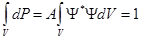 
В квантовой механике принимается, что Ψ и АΨ, где А = const, описывают одно и то же состояние частицы. Следовательно,
|
|
|
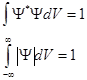
- условие нормировки
интеграл по 
, означает, что он вычисляется по безграничному объему (пронстранству).
y - функция должна быть
1) конечной (так как Р не может быть больше1),
2) однозначной (нельзя обнаружить частицу при неизменных условиях с вероятностью допустим 0,01 и 0,9, так как вероятность должна быть однозначной).
- непрерывной (следует из неприрывности пространства. Всегда имеется вероятность обнаружить частицу в разных точках пространства, но для разных точек она будет разная),
- Волновая функция удовлетворяет принципусуперпозиции: если система может находится в различных состояниях, описываемых волновыми функциями y1,y2...yn, то она может находится в состоянии y, описываемой линейной комбинаций этих функций:
Сn (n=1,2...) - любые числа.
С помощью волновой функции вычисляются средние значения любой физической величины частицы
Уравнение Шредингера
Уравнение Шредингера, как и другие основные уравнения физики (уравнения Ньютона, Максвелла), не выводится, а постулируется. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия точно согласуются с экспериментальными данными.
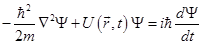(1)
- Временное уравнение Шредингера.
- набла - оператор Лапласа 
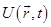- потенциальная функция частицы в силовом поле,
Ψ(y,z,t) - искомая функция
Если силовое поле, в котором движется частица, стационарно (т.е. не изменяется с течением времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера (т.е. Ψ - функция) может быть представлено в виде произведения двух сомножителей - один зависит только от координат, другой - только от времени:
(2)
Е - полная энергия частицы, постоянная в случае стационарного поля.
Подставив (2) ® (1):
|
|
|
(3)
- Уравнение Шредингера для стационарных состояний.
Имеется бесконечно много решений. Посредством наложения граничных условий отбирают решения, имеющие физический смысл.
Граничные условия:
волновые функции должны быть регулярными, т.е.
1)конечными;
2) однозначными;
3) непрерывными.
Решения, удовлетворяющие уравнению Шредингера, называются собственными функциями, а соответствующие им значения энергии - собственными значениями энергии. Совокупность собственных значений называется спектром величины. Если Еn принимает дискретные значения, то спектр - дискретный, если непрерывные - сплошной или непрерывный.
§ 6 Движение свободной частицы
Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.
Уравнение Шредингера для стационарных состояний в этом случае:
Его решение: Ψ(x)= А е ikx, где А = const, k = const
И собственные значения энергии:
Т.к. k может принимать любые значения, то, следовательно, и Е принимает любые значения, т.е. энергетический спектр будет сплошным.
Временная волновая функция
(- уравнение волны)
т.е. представляет плоскую монохромную волну де Бройля.
|
|
|
