Определение остаточных напряжений в сплавах

Упругие остаточные напряжения возникают в металле после пластической деформации и фазовых превращений, термической обработки, облучения частицами высоких энергий и других процессов.

Остаточными напряжениями называются напряжения, которые сохраняются в металле после снятия внешнего воздействия. Различают два вида остаточных напряжений: напряжения I рода (зональные или макронапряжения), которые уравновешиваются в объёме всей детали (изделия). При удалении части детали равновесие между остальными её частями нарушается и деталь под действием макронапряжений деформируется. Напряжения I рода вызывают коробление и растрескивание деталей при их обработке и эксплуатации.

Напряжения II рода (микронапряжения) уравновешиваются в объёмах единичных кристаллов (зёрен) или частей кристаллов, поэтому при разрезании изделия или изготовлении из него образцов микронапряжения не снимаются и не перераспределяются.

Дифракция рентгеновских лучей, как средство определения напряжений, находит широкое применение, так как, по существу, является единственным методом определения остаточных напряжений без разрушения объекта.

Рентгеновский метод позволяет определить только упругие деформации в теле, обусловленные статическими смещениями атомов из положения равновесия. Это вызвано тем, что рентгенографический метод основан на измерении межплоскостных расстояний, которые меняются лишь под действием упругих напряжений, а не в результате пластического сдвига.

Определение макронапряжений в одноосно напряженном теле

Обычно прецизионным методом определяется изменение межплоскостного расстояния в изделии (D d), которое пересчитывается на упругую деформацию e = D d _L / d ₁ = D l / l (рис. 6.1), так как в упруго растянутом теле относительное изменение межплоскостного расстояния d ₁, перпендикулярное приложенной силе, равно общему относительному удлинению тела. Согласно закону Гука, по величине относительной упругой деформации находят величину напряжения, МПа, s = E e, Е – модуль упругости (модуль Юнга).

Р

d ₂

l l ₁

d ₁

Р

 

 

Рис. 6.1

 

 

Для мелкозернистой стали этим методом можно достигнуть высокой точности при D d @ 0,0001Å, s =15…20 МПа.

Первая работа по такой методике была проведена в 1925 г., а в 1929 г. было дано теоретическое обоснование.

 

s₁

N ₁

N ₂ s₂

Плёнка

Нормали к отражающим плоскостям

 

Рис. 6.2

Если на одноосно растянутый образец перпендикулярно к оси приложения нагрузки направить пучок рентгеновских лучей (рис. 6.2), то, изучая отражения под большими углами, можно определить изменение d ₂ (или близкое к нему), связанное с d ₁ посредством коэффициента Пуассона n:

 

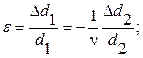(6.1)

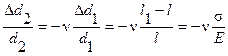. (6.2)

 

Продифференцируем уравнение Вульфа-Брегга 2d sinq =n l по межплоскостному расстоянию d и углу q:

 

D d sinq + d cosqDq = 0;

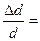- ctgq Dq. (6.3)

Тогда, объединив (6.2) и (6.3), получаем расчетную формулу для одноосно упруго растянутого образца:

 

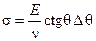. (6.4)

 

В уравнении (6.4) Dq-смещение интерференционной линии на дифракционной картине обусловлено действием макронапряжений.

Измерив смещение линии (с большим углом Вульфа-Брегга ³ 80^о), можно рассчитать s.

Для металлов характеристическое рентгеновское излучение, применяемое в структурном анализе, является малопроникающим. Глубина слоя ~ 50 мкм для любого излучения, включая самое жёсткое Mo (для металлов не легче Ti), поэтому регистрируются напряжения только в поверхностных слоях металла и считается, что при рентгеноструктурном методе исследуется плосконапряженное состояние, так как составляющая к внешней поверхности всегда близка к нулю.