Методы организации поиска отказавших элементов

Основной задачей рациональной организации поиска дефекта является сокращение времени и средств, затрачиваемых на поиск. Это возможно лишь при использовании наиболее совершенных программ поиска дефекта с помощью тестов. Практическая реа­лизация теста состоит в подаче на вход элементов ОД воздейст­вий, имитирующих рабочие сигналы. При этом система выводит­ся из эксплуатации. Предполагается, что исправному состоянию элемента (узла, блока) соответствует наличие сигнала 1 на его вы­ходе, неисправному 0 — его отсутствие. При таком способе поис­ка, как правило, предполагается, что:

■ известны контролируемые параметры (элементы) и формы про­явления отказов, отказ одного из элементов влечет за собой потерю работоспособности ОД;

■ известны экономические характеристики, сопровождающие поиск;

■ подавляющая часть ОД допускает контроль с помощью введе­ния в них контролирующего сигнала.

Среди множества критериев следует выделить две группы: кри­терии информационные и экономические. Физическая интерпре­тация экономических критериев довольно разнообразна: стои­мость проверки или проверочного оборудования, время поиска, число контролируемых элементов, средние потери на решение за­дачи и т. п.

При использовании тестов стремятся к получению минималь­ного числа тестовых воздействий, при которых может быть обнару­жен дефект любого из элементов системы, т. е. наименьшего числа проверок. Нахождению тестов для той или иной системы предше­ствует анализ ее функциональной модели, графическое изображе­ние схемы объекта и построение таблицы неисправностей.

Простейшая схема ОД (ЭА) представлена на рис. 16.2.

Таблица неисправностей этой схемы может быть представлена в виде табл. 16.1 (П обозначает множество всех возможных прове­рок, Е — множество возможных состояний).

Из табл. 16.1 следует, что пять возможных состояний ОД, опре­деляемых состоянием элементов, оказываются полностью различными с помощью четырех проверок.

 

Отказавшие элементы опреде­ляются соответственно кодовыми числами ООН, 1011,1000, 1110.

С ростом числа элементов увеличивается число состояний ОД, а следовательно, и сложность получения оптимальной програм­мы. Минимизация программ может осуществляться известными в теории булевой алгебры методами.

Предположение о равнозначности отказов, что эквивалентно предположению об основной, или последовательной, схеме соеди­нений, дает возможность использовать другие методы построения квазиоптимальных программ поиска дефекта. К ним относятся программы, полученные по методу половинного разбиения. Рас­смотрим особенности этого метода.

Для системы из N последовательно соединенных элементов введем параметры оценки программ поиска дефекта: τ _i — среднее время проверки i -гo элемента; q_i — вероятность отказа системы из-за отказа i -гo элемента.

Величина q_i определяется как вероятность отказа системы при отказе i -гo элемента:

(16.13)

где p_i (t)— вероятность безотказной работы i -гo элемента; p_c(t) — вероятность безотказной работы системы; λ _i — интенсивность от­казов i -гo элемента; λ_с — интенсивность отказов системы.

При малых значениях λt выражение (16.13) приближенно мо­жет быть представлено в виде

(16.14)

или

(16.15)

так как

(16.16)

Задача по поиску неисправного элемента состоит в нахожде­нии такой последовательности проверок, при которой на поиск дефекта затрачивается минимум времени.

Рассмотрим методику построения программы поиска дефек­та при одинаковых значениях q_i и τ _i. Разделим условно систему на две части, содержащие соответственно m и N-m элементов.

Неисправный элемент с вероятностью р ₁= m/N может находить­ся в цепочке из т элементов и с вероятностью p₂ = (N - т)/т в це­почке из N - т элементов.

Математическое ожидание числа неисправных элементов ле­вее/правее точки деления:

(16.17)

Функция (16.17) имеет минимум, т. е. существует такое чис­ло, при котором число неисправных элементов слева и справа от точки деления минимально. Число т,при котором достигается минимум проверок системы, находится из выражения

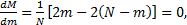(16.18)

в результате т = N/2.

Очевидно, что при этом р ₁ = 0,5 и р ₂ ⁼ 0,5, т. е. отказавший эле­мент с равной вероятностью может находиться как в левой, так и в правой части системы.

Таким образом, при сформулированных условиях оптималь­ный порядок проведения проверок состоит в последовательном делении цепочки элементов пополам. Направление деления каж­дый раз определяется результатом, полученным в точке деления.
При различных q_i и τ_i вероятность неисправности при проверке i -гo элемента составит q.

(16.19)

Для нахождения оптимальной программы поиска дефекта най­дем минимум математического ожидания числа неисправных эле­ментов левее и правее некоторой точки разбиения множества эле­ментов на две части k = т. Математическое ожидание в этом слу­чае составит

или

где

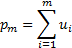
— вероятность нахождения неисправных элементов левее точки m;

— вероятность нахождения неисправных элементов правее точки m. Эти вероятности составляют полную группу несовместных со­бытий

(16.20)

Минимум будет иметь место при

В результате

(16.21)

Решая совместно уравнения (16.20)...(16.21), найдем

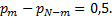(16.22)

Оптимизация программы поиска дефекта состоит в том, что при первом шаге вся цепочка элементов разбивается на две части так, чтобы с вероятностью 0,5 неисправный элемент находился левее или правее некоторой контрольной точки т, в ней произво­дится контроль состояния левой или правой цепочки элементов. Наличие или отсутствие сигнала определяет направление после­дующего деления на отрезки той или иной половины цепочки (с равными значениями вероятностей указанных отрезков цепи элементов).

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Какой процесс называется процессом диагностирования?

2. В чем заключается процесс диагностирования?

3. Для решения каких задач предназначена техническая диагностика?

4. Какими моделями можно описать переход диагностируемого объек­та из одного состояния в другое?

5. Расскажите о математических моделях дискретных систем.

6. Какими моделями описываются системы диагностирования при слу­чайных воздействиях?

7. Назовите методы, с помощью которых организуется поиск отказав­ших элементов.

 

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: