При случайных воздействиях

Рассматриваемые в данном разделе модели свойственны, в ча­стности, некоторым типам систем автоматического управления. К ним относятся, прежде всего, системы со случайно изменяю­щимся управляющим сигналом, а также системы, в которых не­исправности вызывают случайное изменение параметров работо­способности.

Изменение параметров работоспособности данных систем в от­личие от детерминированных не является рядом следующих друг за другом переходов из одного установившегося состояния в дру­гое, но представляет собой случайную функцию. Функция работо­способности, изменяющаяся по случайному закону, определяется статистическими характеристиками — математическими ожида­ниями выходных координат, их дисперсиями, функциями распре­деления вероятностей случайного процесса и другими более слож­ными функционалами, имеющими случайную природу. Эти ха­рактеристики в общем случае зависят от структуры системы, ее элементов и от случайных функций времени, определяющих слу­чайные воздействия на систему.

Математическая модель работоспособности может быть пред­ставлена дифференциальными уравнениями в форме

(16.10)

где t — время; Y_i — компоненты векторной функции работоспособ­ности — координаты системы, по которым производится оценка работоспособности; X_1,..., Х_m — функции времени, изменяющие­ся по случайному закону и характеризующие случайные возмуще­ния и управляющие сигналы; η₁, …,η _l — случайные возмущения, возникающие в системе при неисправности; x₁,..., x_k — случай­ные величины, характеризующие значения параметров элементов системы при той или иной неисправности; — линейные и не­линейные функции соответствующих аргументов.

Математическая модель (16.10) включает практически все си­туации, возможные при оценке влияния неисправностей на рабо­тоспособность системы.

Можно сформулировать основные задачи по анализу работо­способности систем:

1. Анализ работоспособности должен быть направлен на опре­деление степени влияния контролируемых параметров на работо­способность системы и необходим при выборе указанных парамет­ров и при классификации состояний системы по принципу «рабо­тоспособна/неработоспособна».

2. Для системы по заданным вероятностным характеристикам управляющего случайного сигнала при известных вероятностных характеристиках контролируемых параметров необходимо найти вероятностные характеристики работоспособности системы при
заданных ограничениях на условия эксплуатации.

В соответствии с существующими способами упрощения мате­матических моделей систем модель в форме (16.10) может быть представлена как

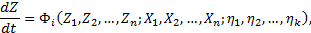
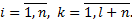(16.11)

Переход к модели (16.11) выполнен в результате замены слу­чайных начальных условий нулевыми при помощи линейного представления переменных в форме

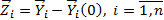и приве­дения случайных функций x_i (t)к выходу.

Анализ работоспособности системы, таким образом, сводится к решению дифференциальных уравнений случайных величин в форме (16.11). Поскольку указанные дифференциальные уравне­ния содержат не только случайные величины, но и случайные функции, возникает задача выбора метода решения. В условиях случайности процессов исследование влияния контролируемых параметров на работоспособность системы сопряжено с рассмот­рением огромного числа вариантов при решении дифференциаль­ных уравнений случайных величин даже для одной конкретной системы. Отсюда вытекают требования к тем методам, которые в наибольшей мере удовлетворяют нуждам практики. Методологи­чески это вынуждает использовать в практике анализа современ­ные ЭВМ. Основным исходным условием, влияющим на весь анализ, является форма представления случайной функции. В класси­ческой теории случайных процессов известны две такие формы.

Случайная функция может рассматриваться как функция двух переменных — времени t и номера опыта s, в котором наблюдает­ся ее реализация:

(16.12)

Очевидно, что реализация случайной функции X (t)во време­ни может рассматриваться либо как совокупность выборочных функций x_s (t), либо как совокупность сечений x_t (s), полученных для фиксированных значений времени. Таким образом, возника­ет альтернативное решение представления функции: либо пред­ставлять ее множеством реализаций x_s (t), либо множеством сече­ний x_t (s), которое может рассматриваться как множество случай­ных величин { x_t (s)}.При прочих условиях, влияющих на выбор формы представления, важным оказывается соображение по прак­тичности представления. В этом случае предпочтение следует от­дать второй форме — представлению случайной величины в виде совокупности случайных величин, реализация которой по ее за­данным вероятностным характеристикам сводится к использова­нию тех или иных ее представлений в виде детерминированных функций случайных величин. При отмеченном подходе, во-пер­вых, появляется возможность широкого использования хорошо разработанных методов получения выборочных значений случай­ных величин по их заданным характеристикам с помощью ЭВМ и, во-вторых, можно пользоваться теми результатами, которые име­ются в теории анализа соответствующих систем.

16.5