 |
Цель: научиться кодировать растровые графические файлы; научиться измерять информационный объем графических файлов.
|
|
|
|
Методические указания.
Графическая информация на экране дисплея представляется в виде изображения, которое формируется из точек (пикселей). Всмотритесь в газетную фотографию, и вы увидите, что она тоже состоит из мельчайших точек. Если это только чёрные и белые точки, то каждую из них можно закодировать 1 битом. Но если на фотографии оттенки, то два бита позволяет закодировать 4 оттенка точек: 00 - белый цвет, 01 - светло-серый, 10 - тёмно-серый, 11 - чёрный. Три бита позволяют закодировать 8 оттенков и т.д.
Количество бит, необходимое для кодирования одного оттенка цвета, называется глубиной цвета.

В современных компьютерах разрешающая способность (количество точек на экране), а также количество цветов зависит от видеоадаптера и может изменяться программно.
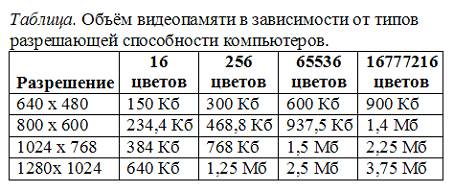
Цветные изображения могут иметь различные режимы: 16 цветов, 256 цветов, 65536 цветов (high color), 16777216 цветов (true color). На одну точку для режима high color необходимо 16 бит или 2 байта.
Наиболее распространённой разрешающей способностью экрана является разрешение 800 на 600 точек, т.е. 480000 точек. Рассчитаем необходимый для режима high color объём видеопамяти: 2 байт *480000=960000 байт.
Для измерения объёма информации используются и более крупные единицы:
Следовательно, 960000 байт приблизительно равно 937,5 Кбайт. Если человек говорит по восемь часов в день без перерыва, то за 70 лет жизни он наговорит около 10 гигабайт информации (это 5 миллионов страниц - стопка бумаги высотой 500 метров).
Скорость передачи информации - это количество битов, передаваемых в 1 секунду. Скорость передачи 1 бит в 1 секунду называется 1 бод.

В видеопамяти компьютера хранится битовая карта, являющаяся двоичным кодом изображения, откуда она считывается процессором (не реже 50 раз в секунду) и отображается на экран.
|
|
|
Задачи:
1. Известно, что видеопамять компьютера имеет объем 512 Кбайт. Разрешающая способность экрана 640 на 200. Сколько страниц экрана одновременно разместится в видеопамяти при палитре: а) из 8 цветов, б) 16 цветов; в) 256 цветов?
2. Сколько бит требуется, чтобы закодировать информацию о 130 оттенках?
3. Подумайте, как уплотнить информацию о рисунке при его записи в файл, если известно, что: а) в рисунке одновременно содержится только 16 цветовых оттенков из 138 возможных; б) в рисунке присутствуют все 130 оттенков одновременно, но количество точек, закрашенных разными оттенками, сильно различаются.
4. Найдите в сети Интернет информацию на тему «Цветовые модели HSB, RGB, CMYK» и создайте на эту тему презентацию. В ней отобразите положительные и отрицательные стороны каждой цветовой модели, принцип ее функционирования и применение.
5. В приложении «Точечный рисунок» создайте файл размером (по вариантам):
А) 200*300, (№ по списку 1, 8, 15, 22, 29)
Б) 590*350, (№ по списку 2, 9, 16, 23, 30)
В) 478*472, (№ по списку 3, 10, 17, 24, 31)
Г)190*367, (№ по списку 4, 11, 18, 25, 32)
Д) 288*577; (№ по списку 5, 12, 19, 26, 33)
Е) 100*466, (№ по списку 5, 13, 20, 27, 34)
Ж) 390*277. (№ по списку 6, 14, 21, 28)
Сохраните его под следующими расширениями:
- монохромный рисунок,
- 16-цветный рисунок,
- 256-цветный рисунок,
- 24-битный рисунок,
- формат JPG.
Используя информацию о размере каждого из полученных файлов, вычислите количество используемых цветов в каждом из файлов, проверьте с полученным на практике. Объясните, почему формула расчета количества цветов не подходит для формата JPG. Для этого воспользуйтесь информацией из сети Интернет.
6. На бумаге в клетку (или в приложении Excel) нарисуйте произвольный рисунок 10*10 клеток. Закодируйте его двоичным кодом (закрашена клетка – 1, не закрашена - 0). Полученный код отдайте одногруппнику для раскодирования и получения изображения.
|
|
|
Лабораторная работа №7. Сжатие текстовой информации. Алгоритм Хаффмана.
Цель работы: научиться сжимать информацию с помощью метода Хаффмана и метода RLE.
Методические указания:
Код Хаффмана
Определение 1: Пусть A={a1,a2,...,an} - алфавит из n различных символов, W={w1,w2,...,wn} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c1,c2,...,cn}, такой что:
| (1) | ci не является префиксом для cj, при i!=j |
| (2) | 
| минимальна (|ci| длина кода ci) |
называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана.
Замечания:
1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.
2. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.
3. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.
Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.
Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.
Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:
1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).
2. Из списка выберем 2 узла с наименьшим весом.
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Добавим сформированный узел к списку.
5. Если в списке больше одного узла, то повторить 2-5.
Приведем пример: построим дерево Хаффмана для сообщения S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".
Для начала введем несколько обозначений:
1. Символы кодируемого алфавита будем выделять жирным шрифтом: A, B, C.
|
|
|
2. Веса узлов будем обозначать нижними индексами: A 5, B 3, C 7.
3. Составные узлы будем заключать в скобки: ((A 5+ B 3)8+ C 7)15.
Итак, в нашем случае A={ A, B, C, D, E, F, G, H }, W={2, 1, 5, 2, 7, 1, 3, 15}.
1. A 2 B 1 C 5 D 2 E 7 F 1 G 3 H 15
2. A 2 C 5 D 2 E 7 G 3 H 15 (F 1+ B 1)2
3. C 5 E 7 G 3 H 15 (F 1+ B 1)2 (A 2+ D 2)4
4. C 5 E 7 H 15 (A 2+ D 2)4 ((F 1+ B 1)2+ G 3)5
5. E 7 H 15 ((F 1+ B 1)2+ G 3)5 (C 5+(A 2+ D 2)4)9
6. H 15 (C 5+(A 2+ D 2)4)9 (((F 1+ B 1)2+ G 3) 5+ E 7)12
7. H 15 ((C 5+(A 2+ D 2)4) 9+(((F 1+ B 1)2+ G 3) 5+ E 7)12)21
8. (((C 5+(A 2+ D 2)4) 9+(((F 1+ B 1)2+ G 3) 5+ E 7)12)21+ H 15)36
В списке, как и требовалось, остался всего один узел. Дерево Хаффмана построено. Теперь запишем его в более привычном для нас виде.
ROOT
/\
0 1
/ \
/\ H
/ \
/ \
/ \
0 1
/ \
/ \
/ \
/ \
/\ /\
0 1 0 1
/ \ / \
C /\ /\ E
0 1 0 1
/ \ / \
A D /\ G
0 1
/ \
F B
Листовые узлы дерева Хаффмана соответствуют символам кодируемого алфавита. Глубина листовых узлов равна длине кода соответствующих символов.
Путь от корня дерева к листовому узлу можно представить в виде битовой строки, в которой "0" соответствует выбору левого поддерева, а "1" - правого. Используя этот механизм, мы без труда можем присвоить коды всем символам кодируемого алфавита. Выпишем, к примеру, коды для всех символов в нашем примере:
| A=0010bin | C=000bin | E=011bin | G=0101bin |
| B=01001bin | D=0011bin | F=01000bin | H=1bin |
Теперь у нас есть все необходимое для того чтобы закодировать сообщение S. Достаточно просто заменить каждый символ соответствующим ему кодом:
S/="0010 1 01000 01001 1 000 011 1 011 1 000 011 0010 1 0011 000 011 011 1 1 1 000 1 1 1 0011 011 0101 1 0101 0101 011 1 000 1 1".
Оценим теперь степень сжатия. В исходном сообщении S было 36 символов, на каждый из которых отводилось по [log2|A|]=3 бита (здесь и далее будем понимать квадратные скобки [] как целую часть, округленную в положительную сторону, т.е. [3,018]=4). Таким образом, размер S равен 36*3=108 бит
Размер закодированного сообщения S/ можно получить воспользовавшись замечанием 2 к определению 1, или непосредственно, подсчитав количество бит в S/. И в том и другом случае мы получим 89 бит.
Итак, нам удалось сжать 108 в 89 бит.
Теперь декодируем сообщение S/. Начиная с корня дерева будем двигаться вниз, выбирая левое поддерево, если очередной бит в потоке равен "0", и правое - если "1". Дойдя до листового узла мы декодируем соответствующий ему символ.
|
|
|
Ясно, что следуя этому алгоритму мы в точности получим исходное сообщение S.
Метод RLE.
Наиболее известный простой подход и алгоритм сжатия информации обратимым путем - это кодирование серий последовательностей (Run Length Encoding - RLE). Суть методов данного подхода состоит в замене цепочек или серий повторяющихся байтов или их последовательностей на один кодирующий байт и счетчик числа их повторений. Проблема всех аналогичных методов заключается лишь в определении способа, при помощи которого распаковывающий алгоритм мог бы отличить в результирующем потоке байтов кодированную серию от других - некодированных последовательностей байтов. Решение проблемы достигается обычно простановкой меток в начале кодированных цепочек. Такими метками могут быть, например, характерные значения битов в первом байте кодированной серии, значения первого байта кодированной серии и т.п. Данные методы, как правило, достаточно эффективны для сжатия растровых графических изображений (BMP, PCX, TIF, GIF), т.к. последние содержат достаточно много длинных серий повторяющихся последовательностей байтов. Недостатком метода RLE является достаточно низкая степень сжатия или стоимость кодирования файлов с малым числом серий и, что еще хуже - с малым числом повторяющихся байтов в сериях.
Сжатие методом Хаффмана
«Какая зима золотая!
Как будто из детских времен...
Не надо ни солнца, ни мая –
пусть длится торжествениый сон.
Пусть я в этом сне позабуду
когда-то манивший огонь,
И лето предам, как Иуда,
за тридцать снежинок в ладонь.
Затем, что и я холодею,
тепло уже страшно принять:
я слишком давно не умею
ни тлеть, ни гореть, ни сжигать…
Все чаще, все дольше немею:
К зиме уже дело, к зиме...
И только того отогрею,
кому холоднее, чем мне»
|
|
|


