 |
Формулы связи координат соответственных точек горизонтального и наклонного снимков, полученных из одного центра проекции (формулы трансформирования координат точек снимка)
|
|
|
|
Пусть из точки S получен наклонный Р и горизонтальный Р0 снимки, на которых точка М объекта изобразилась соответственно в точках m и m0 (рис.1.6.1). Найдем зависимости между координатами этих точек.
 |
Рис.1.6.1
На рис.1.6.1 
и 
– векторы, определяющие положение точек m и m0 относительно центра проекции S на снимках Р и Р0.
Векторы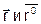 
коллинеарные, поэтому можно записать:
; (1.6.1)
где N - скаляр.
В системе координат горизонтального снимка Sx0y0z0 выражение (1.6.1) имеет вид (полагая х0=у0=0):
; (1.6.2)
где x0y0z0 –координаты вектора 
в системе координат горизонтального снимка.
; (1.6.3)
Из третьего уравнения (1.6.2) следует, что
.
Подставив значение N в первые два уравнения (1.6.2) получим формулы связи координат соответственных точек горизонтального и наклонного снимков:
; (1.6.4)
которые с учетом (1.6.3) имеют вид:
. (1.6.5)
Выведем формулы определения координат точек наклонного снимка по координатам соответственных точек горизонтального снимка.
Из (1.6.1) следует, что
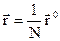. (1.6.6)
В системе координат наклонного снимка Sxyz (1.6.6) имеет вид:
; (1.6.7)
где х*,y*,z* - координаты вектора 
в системе координат наклонного снимка.
; (1.6.8)
Из третьего уравнения (1.6.7) следует, что
Подставив значение 1/N в первые два уравнения (1.6.7), получим формулы связи координат точек наклонного и горизонтального снимков.
(1.6.9)
(1.6.10)
 |
1.7 Формулы связи координат точек местности и их изображений на стереопаре снимков (прямая фотограмметрическая засечка).
Рис.1.7.1
p=x1-x2 – продольный параллакс; q=y1-y2 – поперечный параллакс.
 |
Рис.1.7.2
На рис.1.7.2 показана стереопара снимков Р1 и Р2, на которых точка местности М изобразилась соответственно в точках m1 и m2. Будем считать, что элементы внутреннего и внешнего ориентирования снимков известны.
|
|
|
Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков.
Из рис.1.7.2 следует, что векторы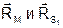 
определяют соответственно положение точки местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор 
определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.
Векторы 
определяют положение точек m1 и М относительно центра проекции S1. Векторы 
определяют положение точек m2 и М относительно центра проекции S2.
Из рис.1.7.2 следует, что
(1.7.1)
Так как векторы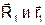 
коллинеарные, то
; (1.7.2)
где N – скаляр.
С учетом (1.7.2) выражение (1.8.1) будет иметь вид
. (1.7.3)
В координатной форме выражение (1.7.3) будет иметь вид
; (1.7.4)
где X1’,Y1’,Z1’ –координаты вектора 
в системе координат объекта OXYZ.
.
Найдем значение N, входящее в выражение (1.7.4). Из рис.1.7.2 следует, что
;
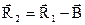или с учетом (1.7.2)
. (1.7.5)
Так как векторы 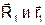коллинеарны, то их векторное произведение
. (1.7.6)
С учетом (1.7.5) выражение (1.7.6) можно представить в виде
;
или
. (1.7.7)
Выражение (1.7.7) можно представить в виде
;
или
; (1.7.8),
где
- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;
BX, BY, BZ, X1’, Y1’, Z1’, X1’, Y1’, Z1’ – координаты векторов 
в системе координат объекта OXYZ.
;
где i – номер снимка, а
. (1.7.9)
Так как векторы 
коллинеарные (потому что векторы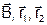 
компланарны), значение N можно найти как отношение их модулей, то есть
; (1.7.10)
В координатной форме выражение (1.7.10) с учетом (1.7.8) имеет вид
; (1.7.11)
У коллинеарных векторов отношение их координат равно отношению их модулей, поэтому можно записать, что:
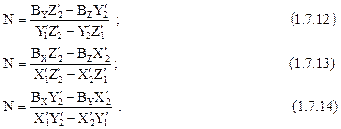
Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках координаты сооветственныхточек x1,y1 и x2,y2, то сначала надо определить по одной из формул (1.7.12)-(1.7.14) значение скаляра N, а затем по формуле (1.7.4) вычислить координаты точки местности X,Y,Z.
|
|
|
|
|
|
