Внешнее ориентирование модели. Элементы внешнего ориентирования модели.

Рис.1.13.1

 

О_МХ_МY_MZ_M - система координат фотограмметрической модели;

OXYZ - система координат объекта;

А  - точка объекта

А_М - соответствующая точке А объекта точка фотограмметрической модели.

Векторы определяют положение начала системы координат модели О_МХ_МY_MZ_M и точки А местности относительно начала системы координат объекта OXYZ.

Векторы определяют соответственно положение точек А_М и А относительно системы координат фотограмметрической модели.

Из рис.1.13.1 следует, что

. (1.13.1)

Векторы коллинеарные, поэтому

 

; (1.13.2)

 

где t – знаменатель масштаба модели.

С учетом (1.13.2) выражение (1.13.1) имеет вид:

 

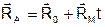; (1.13.3)

 

В координатной форме выражение (1.13.3) имеет вид:

 

; (1.13.4)

или

. (1.13.5)

 

В выражениях (1.13.4) и (1.13.5):

X, Y, Z – координаты точки объекта в системе координат объекта;

Х_М, Y_M, Z_M - координаты соответствующей точки модели в системе координат фотограмметрической модели;

А_М – матрица преобразования координат, элементы a_ij которой являются функциями углов w_М, a_М, À_М, определяющих ориентацию системы координат модели относительно системы координат объекта;

t – знаменатель масштаба модели.

7 параметров: - называют элементами внешнего ориентирования модели.

 

1.14 Определение элементов внешнего ориентирования модели по опорным точкам.

Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения (1.13.5), которые представим в виде:

. (1.14.1)

Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения (1.14.1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения (1.14.1), а каждая высотная опорная точка (Z) – третье уравнение из выражения (1.14.1).

Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.

Так как уравнения (1.14.1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.

 

. (1.14.2)

 

В уравнении поправок:

a_i, b_i, c_i – частные производные от уравнений (1.14.1) по соответствующим переменным;

ℓ_X, ℓ_Y, ℓ_Z – свободные члены.

Значения коэффициентов уравнений поправок a_i, b_i, c_i вычисляют по известным значениям координат Х_М, Y_M, Z_M и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓ_X, ℓ_Y, ℓ_Z вычисляют таким же образом по формулам (1.14.1).

Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием V^TPV=min).

 

1.15 Определение элементов внешнего ориентирования снимков стереопары.

 

По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.

Линейные элементы внешнего ориентирования снимков определяют по формулам:

; (1.15.1)

 

в которых - координаты центра проекции i-го снимка стереопары в системе координат модели.

Угловые элементы внешнего ориентирования снимков w_i, a_i, À_i определяют в следующей последовательности:

1. Сначала получают матрицу преобразования координат i-го снимка

 

; (1.15.2)

 

А_М – матрица, в которой элементы a_ij вычисляют по угловым элементам внешнего ориентирования модели w_М, a_М, À_М;

A_i’ – матрица, в которой элементы a_ij вычисляют по угловым элементам взаимного ориентирования i-го снимка w_i’, a_i’, À_i’.

2. Затем по элементам a_ij матрицы A_i вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:

 

.

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: