 |
Примеры контрольных вопросов
|
|
|
|
Литература с указанием страниц, необходимая для ответов на контрольные вопросы, приведена в разделе 6. Смысловое деление материала в контрольных вопросах такое же, как при изложении содержания теоретической части (раздел 6).
О п р е д е л е н и е, п а р а м е т р ы, с в о й с т в а ЛЭ и ЛЦ, о с н о в н ы е з а к о н ы и ММЦ л и н е й н ы х ц е п е й:
1) дайте определение линейного элемента и линейной цепи; укажите их свойства;
2) назовите режимы работы электрических цепей, дайте определение, поясните условия их существования;
3) запишите компонентные уравнения и выражение мгновенной мощности для линейных L -, C -, R -элементов;
4) запишите уравнения баланса токов, баланса напряжений и баланса мощностей через мгновенные значения токов и напряжений и поясните:
а) в каком режиме, при каком характере воздействия, для какого типа цепей они справедливы,
б) каким образом каждое из балансных уравнений участвует в анализе цепей;
5) дайте понятие математической модели цепи и укажите ее возможные варианты;
6) запишите в общем виде дифференциальное уравнение ЛЦ (с сосредоточенными параметрами), охарактеризуйте его;
7) сформулируйте принцип наложения, дайте графическую иллюстрацию;
8) запишите выражение для гармонического колебания, укажите его параметры, покажите на основе компонентных уравнений линейных элементов замечательное свойство гармонических колебаний сохранять свою форму;
9) изобразите три гармонических колебания с амплитудой 10 В, частотой 1 кГц и начальными фазами 0о, 60о, -60о;
10) укажите, к какому значению стремится косинусоидального колебания с параметрами U = 20 B, частота 10 кГц, φ0=00 увеличении периода колебания (Т ®¥);
11) дайте определение идеальных и реальных источников (генераторов) тока и напряжения, независимых и зависимых источников сигнала;
|
|
|
12) запишите выражения всех токов и напряжений на элементах при действии п о с т о я н н ы х э.д.с. (e (t) = E), если параметры схем и значения Е заданы (рис. 9.1);
13) запишите ММЦ по МТВ для схем рис. 9.1 при действии источников e (t):
а) произвольной формы,
б) гармонического характера одинаковой частоты.
.
М е т о д к о м п л е к с н ы х а м п л и т у д:
14) изложите общие принципы символических методов, алгоритм работы, преимущества символических методов;
15) сформулируйте, какие изменения и почему претерпевает ММЦ в виде дифференциального уравнения при использовании метода комплексных амплитуд;
16) изложите суть перехода от гармонической функции времени к комплексному числу, т.е. цепочку «гармоническое колебание – его представление через проекцию вращающегося вектора – представление в виде точки на комплексной плоскости», поясните взаимную неподвижность векторов, отображающих любые токи и напряжения в цепи, на которую действует источник гармонического колебания;
17) 
A, запишите İ, İm, I, Im и правильно их назовите, укажите, как связаны I и Im;
18) поясните, что такое оператор вращения, когда и почему его можно опустить; запишите его по данным предыдущего пункта;
19) запишите i (t), u (t), İm, Ům, если
а) I = 50 А, частота 104 Гц, начальная фаза 75о,
б) Um = 70 B, частота 105 рад/c, начальная фаза p/2,
в) 
А, частота 500 Гц;
20) сформулируйте, что такое комплексное сопротивление участка цепи, закон Ома в комплексной форме, покажите общность вида компонентных уравнений для R -, L -, C -элементов в комплексной форме;
21) индуктивность L =10 мГн находится под гармоническим напряжением с параметрами: амплитуда 10 В, частота 1 кГц, начальная фаза 0о; вычислите сопротивление индуктивности, ток через индуктивность и фазовый сдвиг между током и напряжением двумя способами;
|
|
|
а) методом комплексных амплитуд,
б) на основе компонентных соотношений для uL, iL;
результаты сравните и поясните;
22) через емкость С = 0,1 мкФ протекает косинусоидальный ток с параметрами: амплитуда 10 мА, частота 104 рад/с, начальная фаза 0о; вычислите сопротивление емкости, падение напряжения и фазовый сдвиг между током и напряжением двумя способами:
а) методом комплексных амплитуд,
б) на основе компонентных уравнений для uC, iC;
результаты сравните и поясните;
23) запишите законы Кирхгофа в комплексной форме и укажите, при каких условиях справедлива такая запись;
24) три источника гармонических колебаний одинаковой частоты, действуя по отдельности, создают на линейном сопротивлении R следующие напряжения:
В,
В,
В,
определите падение напряжения от одновременного действия сразу трех источников, изобразите схему подключения источников к сопротивлению R;
25) с узлом схемы связаны три тока (рис. 9.2), используя МКА, вичислите ток i 3(t), если
,
;
26) дайте определение средней мощности РСР, получите выражение РСР, укажите значение РСР для индуктивности, емкости и сопротивления, поясните, почему средняя мощность называется активной;
27) запишите все возможные выражения для комплексной мощности в двухполюснике Z=R+jX, если гармонический ток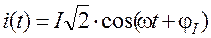 
вызывает на нем падение напряжения 
;
28) запишите баланс мощностей в комплексной форме;
29) изобразите треугольники сопротивлений, проводимостей, мощностей, обозначьте активные и реактивные составляющие, запишите типовые соотношения между модулем, аргументом, активной и реактивной составляющими в любом из перечисленных треугольников;
30) вычислите значения 
каждого элемента схемы рисунка 9.3, если сопротивления указаны в омах, 
A, 
A, 
B.
Э к в и в а л е н т н ы е п р е о б р а з о в а н и я:
31) сформулируйте условие эквивалентности двух участков цепи;
32) докажите, что полное сопротивление цепи, состоящей из n последовательно соединенных сопротивлений Zi, определяется как
;
33) докажите, что полная проводимость двухполюсника из n параллельно соединенных ветвей с проводимостями Yi определяется как
;
34) найдите полную емкость двухполюсника, состоящего из последовательно соединенных четырех разных емкостей, четырех одинаковых емкостей, двух разных емкостей, двух одинаковых емкостей;
|
|
|
35) сформулируйте правило для определения сопротивления двухполюсника, содержащего четыре параллельные ветви с разными сопротивлениями Z, выделите частный случай параллельного соединения двух равных сопротивления, выделите частный случай параллельного соединения k одинаковых сопротивлений;
36) найдите полную емкость двухполюсника, состоящего из параллельно соединенных трех одинаковых емкостей, трех разных емкостей;
37) аналогичный вопрос для индуктивности;
38) назовите условия, лежащие в основе пересчета звезды в треугольник сопротивлений и наоборот, сделайте необходимые обозначения на моделях;
39) поясните, почему нельзя эквивалентно пересчитать источник тока в источник напряжения;
40) пересчитайте генератор напряжения в генератор тока так, чтобы число узлов не увеличилось (рис. 9.4);
41) вычислите входное (эквивалентное) сопротивление для следующих двухполюсников:
42) на моделях рис. 9.6 сопротивления отдельных участков указаны в омах, вычислите входное сопротивление двухполюсников;
43) поясните смысловое значение чисел, указанных для индуктивностей и емкостей на рис. 9.5 и рис. 9.6;
44) вычислите входные сопротивления двухполюсников рис. 9.5, 9.6 и рис. 9.10 на крайних частотах диапазона w = 0 и w®¥;
45) участок цепи на частоте 103 рад/с имеет сопротивление Z =2× e -j60º Ом, изобразите последовательную модель замещения для этого участка, постройте в относительном масштабе треугольник сопротивлений, определите эквивалентные параметры этого участка;
46) по данным предыдущего вопроса рассчитайте параллельную модель замещения участка, постройте с соблюдением относительного масштаба треугольник проводимостей, рассчитайте эквивалентные параметры для параллельной схемы замещения;
47) постройте векторную диаграмму токов и напряжений для параллельной модели участка цепи с сопротивлением Z = 0,25×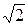 
× ej 45º Ом, если входной ток этого участка 
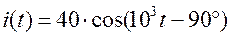мА;
48) обозначив встречное включение «*», согласное «×» изобразите последовательное соединение двух связанных индуктивностей L 1 и L 2, запишите выражение для расчета LЭКВ;
|
|
|
49) тот же вопрос для параллельного соединения.
М е т о д ы р а с ч е т а э л е к т р и ч е с к и х ц е п е й:
50) запишите типовую ММЦ по методу контурных токов с необходимыми пояснениями обозначений и знаков
а) в виде системы линейных уравнений,
б) в матричной форме;
51) тот же вопрос по методу узловых потенциалов;
52) сформулируйте закон, лежащий в основе каждого уравнения, составленного
а) по методу контурных токов,
б) по методу узловых потенциалов;
53) дайте определение независимого контура, покажите на конкретном примере, как практически в сложной схеме определить число независимых контуров;
54) поясните, почему в методе узловых потенциалов можно сказать «узловой потенциал» и «узловое напряжение», ведь потенциал и напряжение - это разные понятия;
55) для контура, указанного преподавателем на схеме рис. 2.1, составьте уравнение по второму закону Кирхгофа, а затем преобразуйте его к типовой форме, поясните получившееся правило знаков и условия, когда оно выполняется;
56) для узла, указанного преподавателем на схеме рис. 2.1, составьте уравнение по первому закону Кирхгофа и преобразуйте его к типовой форме, поясните получившееся правило знаков и условия, когда оно выполняется;
57) поясните, почему в схеме с n узлами составляется только (n-1) уравнение по первому закону Кирхгофа;
58) на рис. 9.7 приведена топология (структура) фрагмента цепи с указанием направления токов, выразите токи ветвей через контурные, определите, с какими знаками взаимные сопротивления войдут в систему уравнений по МКТ и почему;
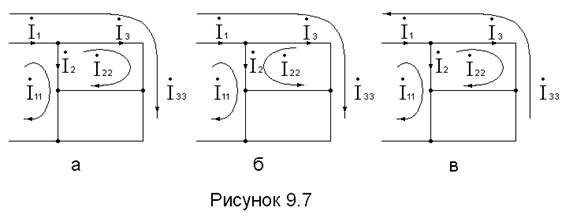
59) выразите токи ветвей (рис. 9.8) через узловые потенциалы;
60) являются ли вспомогательные расчетные величины «контурные токи» и «узловые потенциалы» физически существующими, можно ли их измерить; каков смысл использования их для расчета?
61) если рассчитывается ток одной ветви, выгоднее опорным выбрать узел, соединенный с этой ветвью, поясните, почему; как следует выбирать опорный узел в общем случае, когда рассчитываются все токи?
62) изложите порядок действий при расчете методом контурных токов при использовании типовой системы;
63) то же при расчете методом узловых напряжений;
64) изобразите схему цепи по заданной типовой ММЦ
(R 1 +R 2) ×İ 11 – R 2 ×İ 22 = Ė 1
– R 2 ×İ 11 + (R 2 +j w L 1 + 
) ×İ 22 – j w L×İ 33 = Ė 2
– j w L 1 ×İ 22 + (R 3 + j w L 1 + j w L 3) ×İ 33 = Ė 2 – Ė 3
65) изобразите схему цепи по заданной типовой ММЦ
66) изложите алгоритм получения ММЦ по МУП (МКТ), если в схеме имеется зависимый источник; поясните как получить матрицу проводимостей (сопротивлений), включающую параметры зависимого источника;
|
|
|
67) в схему между узлами 3 и 4 (рис. 9.9) включен зависимый источник тока jк, управляемый током iЭ (jK=α×iЭ) или напряжением uЭ (jK=S×uэ)
а) выразите ток зависимого источника jK через соответствующие узловые потенциалы,
б) в какие уравнения системы по МУП и с какими знаками войдет зависимый источник jK,
в) каким образом войдет крутизна зависимого источника S в собственные и взаимные проводимости узлов?
68) зависимый источник 
включен между первым и опорным (нулевым) узлом, «подтекая» к опорному узлу; поясните, каким образом (в какие ячейки и с какими знаками) крутизна S войдет в матрицу проводимостей при расчете по МУП;
69) матрица проводимостей, поставленная по МУП, включает крутизну зависимого источника S следующим образом: Y 22– S, Y 32+ S, дайте два правильных варианта ответа как и между какими узлами на схеме включен зависимый источник тока и «протекает» управляющий ток;
70) сформулируйте теорему об эквивалентном генераторе; изложите возможные способы определения ĖЭГ и ZЭГ.
71) пусть для схемы рис. 9.10 с заданными параметрами L, С, R ток через индуктивность на некоторой частоте f 0 источника гармонического колебания Ė известен (измерен или рассчитан по теореме об эквивалентном генераторе); изложите порядок расчета всех остальных токов на этой же частоте, введя необходимые обозначения.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРЫ
1. Попов В.П. Основы теории цепей. – М.: Высш.шк.,1985.-496с.
2. Лосев А.К. Теория линейных электрических цепей. – М.: Высш. шк., 1987.-511с.
3. Атабеков Г.И. Основы теории цепей. – СПб.: Лань.2006.-424с.
4. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. – Л.:
Энергия,1972.-816с.
5. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. – М.: Л.:
Энергия, 1965.-892с.
6. Белецкий А.Ф. Теория линейных электрических цепей. – М.:
Радио и связь,1986.-543с.
7. Матханов П.Н. Основы анализа электрических цепей.
Линейные цепи. – М.: Высш.кш.,1972.-335с.
8. Афанасьев Б.П., Гольдин О.Е., Кляцкин И.Г., Пинес Г.Я.
Теория линейных электрических цепей. – М.:Высш.шк., 1973.-592с.
9. Попов В.П. Основы теории цепей. – М.: Высш.шк.,2000.-575с.
10. Попов В.П. Основы теории цепей. – М.: Высш.шк.,2003.-576с.
Учебное издание
И.В. Мельникова
МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ
И РАСЧЕТА СЛОЖНОЙ ЛИНЕЙНОЙ
|
|
|
