 |
2.4.3. Определение передаточной функции произвольной схемы
|
|
|
|
2. 4. 3. Определение передаточной функции произвольной схемы
| R0 |
| R1 |
| C |
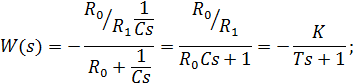

Таким образом, эта схема имеет свойства апериодического звена.
Рассмотрим более сложную схему
| R2 |
| R1 |
| C2 |
| C1 |


2. 4. 4. Реализации фильтровых звеньев
Существует два типа таких структур с многопетлевыми обратными связями:
Структура Рауха
| A1 |
| Z1 |
| Z2 |
| Z3 |
| Z4 |
| Z5 |
| UВХ |
| UВЫХ |
Её передаточная функция

Если подставить вместо Z резисторы и конденсаторы, то получим:
Колебательное звено (ФНЧ второго порядка):
| C1 |
| C2 |
| R3 |
| R1 |
| A1 |
| R2 |
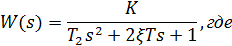

Полосовой фильтр:
| C1 |
| C2 |
| R3 |
| R1 |
| A1 |
| R2 |
| UВХ |
| UВЫХ |

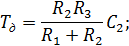
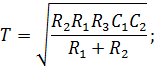

С комбинированной обратной связью (структура Саллен-Ки, Sallen-Key)
| Z1 |
| Z2 |
| Z3 |
| Z4 |
| UВХ |
| UВЫХ |
| Z5 |
| Z6 |

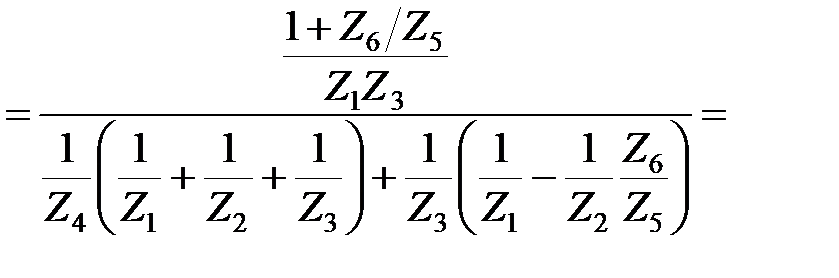
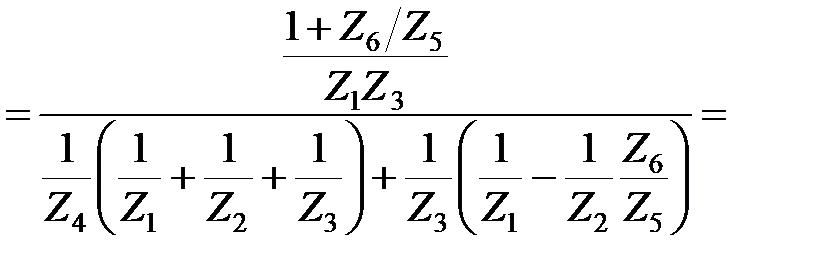
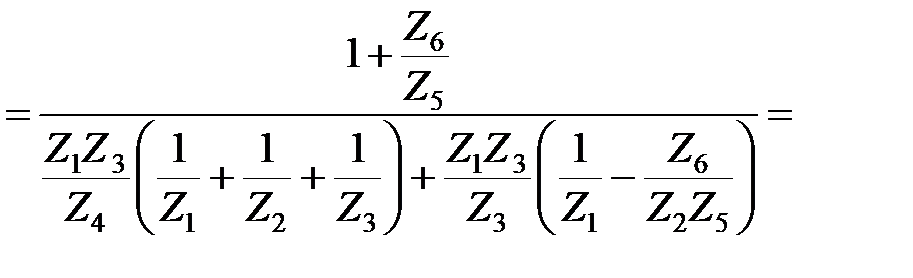


| Z1 |
| Z3 |
| Z2 |
| Z4 |
| UВХ |
| UВЫХ |

ФНЧ: 
| R1 |
| C1 |
| R2 |
| C2 |
| UВХ |
| UВЫХ |
| R3 |
| R4 |

Для усилителя с единичным коэффициентом передачи  и
и
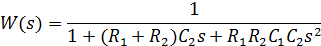
| R1 |
| C1 |
| R2 |
| C2 |
| UВХ |
| UВЫХ |
примем: 
Тогда 
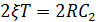

Алгоритм расчёта:
Выбираем R из стандартного ряда.
Тогда  ;
;
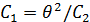
2. 5. Аналоговая реализация произвольных передаточных функций
Методика воспроизведения динамики объектов (например, корректирующих звеньев) средствами аналоговой схемотехники была разработана применительно к моделированию динамических систем на аналоговых вычислительных машинах. Эта методика с минимальными изменениями применима к современным условиям при реализации динамических звеньев с помощью интегральных операционных усилителей, а также и при моделировании динамики систем с помощью цифровых вычислительных машин.
|
|
|
Можно выделить следующие основные этапы подготовки задачи моделирования.
1. Предварительная подготовка – приведение исходных математических соотношений к виду, удобному для моделирования.
Должны быть заданы или определены на данном этапе:
цель исследования
математическая модель;
размерности параметров (переменных),
начальные значения, оценки диапазонов изменения переменных и их производных;
указаны параметры, которые должны варьироваться в процессе работы схемы;
известные решения данной (подобной) задачи и методы оценки правильности решения.
2. Составление функциональной схемы моделирования:
Для этого исходные уравнения необходимо преобразовать к виду, удобному для представления с применением аналоговых функций - обычно в виде систем уравнений первого порядка, либо уравнения, разрешённого относительно старших производных.
Иногда исходная математическая модель может быть представлена как совокупность передаточных функций (дифференциальных уравнений) типовых звеньев.
В процессе преобразования исходных уравнений могут быть введены новые (промежуточные, вспомогательные) переменные.
По мере возможности осуществляется упрощение схемы, и проверяется её соответствие заданным математическим соотношениям.
3. Выбор масштабов переменных и масштаба времени.
При этом осуществляется запись машинных уравнений (с учётом масштабных коэффициентов и машинных переменных). Должны быть заданы также масштабы начальных условий и ограничений.
4. Расчет коэффициентов передачи решающих блоков.
Осуществляется с учётом масштабных соотношений, критериев аналогии и схемы реализации математических соотношений. На этом этапе может осуществляться коррекция значений масштабных коэффициентов.
5. Составление принципиальной схемы.
Осуществляется выбор конкретных решающих элементов, элементов входных цепей и цепей обратной связи, цепей задания начальных условий и др. с учётом удобства задания и изменения параметров в процессе решения задачи.
|
|
|
Примечание:
Следует избегать:
замкнутых контуров, в которые не входят интеграторы;
Коэффициентов передачи более 10…30
Использования числа интеграторов большего, чем необходимо.
ПРИМЕР:
|
|
|


