 |
При последовательном соединении звеньев их передаточные функции перемножаются.
|
|
|
|
Понятие чувствительности
Чувствительность автоматических систем характеризует влияние изменений параметров элементов на их свойства. Вариации элемента автоматической системы приводит к изменению его передаточной функции, а это в свою очередь вызывает изменение передаточной функции всей замкнутой автоматизированной системы, а значит, в конечном итоге, и изменение величин, характеризующих ее состояние. Для количественного учета всех этих служат функции чувствительности
Из выражения видно, что чем меньше чувствительность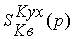 
или функция чувствительности, тем меньше влияние передаточной функции Kв(p) рассматриваемого элемента на свойства автоматической системы. Говоря об уменьшении или увеличении чувствительности, мы всегда будем подразумевать уменьшение или увеличение ее модуля. Естественно, что чем меньше чувствительность автоматической системы, тем система более высококачественна. Поэтому большой интерес представляют такие структуры автоматических систем, которые обладают малой чувствительностью.
Из основной формулы чувствительности можно установить два пути уменьшения чувствительности автоматических систем.
Первый путь состоит в таком изменении передаточной функции системы Kyx(p), при котором она приближалась бы к передаточной функции части системы, не зависящей от варьируемого элемента. По существу этот путь связан с компенсацией изменений варьируемого элемента, т.е. с изменением эффекта, вызываемого вариацией элемента, и созданием соответствующего компенсирующего воздействия. Классическим примером реализации этого пути является известная мостовая схема компенсации.
Второй путь состоит в увеличении усиления элементов контура обратной связи. При стремлении усиления к бесконечности чувствительность по отношению к управляемому объекту будет стремиться к нулю.
|
|
|
Математические модели объектов и систем управления
Под моделью понимают такой материально или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал и отражает отдельные, ограниченные в нужном направлении стороны явления рассматриваемого процесса. Таким образом, математическая модель – это приближенное отображение моделируемой системы с помощью уравнений и ограничивающих условий. Математическое описание основывается на физических, химических, энергетических и других закономерностях.
В общем случае порядок исследования САУ включает математическое описание системы и изучение ее переходных и установившихся режимов. Получение математической модели начинается с разбиения системы на звенья и описания этих звеньев.
Звеном направленного действия называют звено, передающее воздействие только в одном направлении – со входа на выход, так что изменение состояния такого звена не влияет на состояние предшествующего звена, работающего на его вход. Соответственно математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.
В результате разбиения САУ на звенья направленного действия и получения математического описания отдельных звеньев составляется структурная схема системы, которая и является ее математической моделью.
Преобразование Лапласа
В настоящее время под операционным исчислением понимают совокупность методов прикладного математического анализа, позволяющих экономными средствами получать решения линейных дифференциальных уравнений, а также разностных и некоторых типов интегральных уравнений.
|
|
|
Операционное исчисление нашло широкое применение в теории автоматического регулирования, где с его помощью производится анализ переходных и установившихся процессов в автоматических системах. Сущность операционного метода заключается в использовании прямого преобразовании Лапласа (ППЛ ), которое некоторой функции 
действительной переменной t ставит в соответствие функцию 
комплексной переменной p:
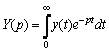, где 
– переменная (множитель) Лапласа.
Передаточная функция
Таким образом, передаточная функция полностью характеризует динамические свойства системы и поэтому является ее важнейшей характеристикой. Зная передаточную функцию системы, можно определить процесс изменения выходной координаты системы при наличии входного воздействия и заданных начальных условиях.
Преобразование структурных схем САУ. Отдельные звенья САУ могут быть соединены друг с другом в различных комбинациях. Зная передаточные функции звеньев, образующих сложную систему c заданной структурной схемой, можно получить передаточную функцию системы в целом, учитывая следующие правила преобразования.
При последовательном соединении звеньев их передаточные функции перемножаются.
|
|
|
