Особенности математического описания цифровых систем управления, анализа и синтеза систем управления с ЭВМ в качестве управляющего устройства

Возрастание требований к качеству работы САУ, увеличение объема перерабатываемой информации, усложнение объектов управления привели к тому, что средствами аналоговой техники и непрерывной автоматики нельзя решить многие практические задачи. В результате в современных САУ стали широко использовать цифровые системы, в состав которых входят ЦВМ или специализированные цифровые устройства. Быстрое внедрение в технику цифровых систем объясняется тем, что они по сравнению с аналоговыми имеют значительно большие вычислительные возможности. В цифровых системах, выполненных на базе микроэлектроники (интегральных схемах, микропроцессорах и мини-ЭВМ), при небольших массах и габаритах можно использовать более сложные алгоритмы обработки сигналов. При этом точность реализации алгоритмов определяется только периодом дискретизации, числом разрядов цифровых кодов и может быть сделана весьма высокой. Важным преимуществом цифровых систем является высокая стабильность их работы, в них отсутствует дрейф нуля дискретизаторов и других цифровых устройств систем. Кроме того, в цифровых системах просто осуществляется перестройка их структуры и регулировка параметров.

В процессе преобразования непрерывных сигналов 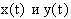в цифровые происходит дискретизация этих сигналов, то есть осуществляется выборка непрерывных сигналов, соответствующих дискретным моментам времени (обычно выборка производится через равные промежутки времени Т). В процессе преобразования сигналов в цифровую форму происходит также их квантование по уровню. В результате из всех возможных дискретных сигналов выбираются только разрешенные уровни, кратные шагу квантования, равному значению младшего разряда ЦВМ. Если преобразователь НК имеет a разрядов, то число уровней квантования, отличных от нуля, составляет

Квантование сигналов по уровню – нелинейная операция, поэтому цифровые системы относятся к классу нелинейных.

Цифровые системы с дискретизацией в них сигналов по времени относятся к дискретным. Дискретизация сигналов – линейная операция, поэтому, пренебрегая шумом квантования, цифровую систему можно рассматривать как линейную дискретную систему, методы анализа которой рассматриваются в данном разделе.

Входные и выходные сигналы цифровой части системы являются числовыми последовательностями. При анализе можно отвлечься от физических принципов работы цифровых устройств и считать основной характеристикой ЦВМ алгоритм, в соответствии с которым входные сигналы преобразуются в выходные. Тогда ЦВМ в САУ можно представить как последовательное соединение цифрового фильтра, осуществляющего преобразование сигналов, и звена запаздывания с передаточной функцией . Звено запаздывания учитывает время прохождения сигнала через цифровой фильтр. Время запаздывания зависит от решаемого алгоритма и быстродействия ЦВМ, в общем случае оно не равно периоду выдачи данных с ЦВМ. Очевидно, что эти величины связаны соотношением . Знак равенства имеет место в том случае, когда ЦВМ обслуживает один канал.

Для математического описания преобразования непрерывного сигнала в дискретный удобна следующая математическая модель сигнала:

Cигнал называют обобщенным дискретным сигналом. Этот сигнал представляет собой последовательность d-функций, площади которых равны значениям непрерывного сигнала в дискретные моменты времени t=0,T,2T,.... Преобразование непрерывного сигнала в последовательность мгновенных импульсов (141) можно рассматривать как модуляцию последовательности единичных импульсов непрерывным сигналом (рис. 28). На структурных схемах цифровых САУ процесс преобразования сигнала x(t) в отображается введением ключа, который называют дискретизатором или простейшим импульсным элементом.

Последовательность мгновенных импульсов подается на цифровое устройство системы, в котором перерабатывается в соответствии с алгоритмом в выходную последовательность мгновенных импульсов 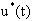. В САУ с непрерывными объектами управления последовательность импульсов 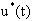преобразуется в непрерывный сигнал. Для этой цели применяются преобразователи, сигнал на выходе которых меняется дискретно. В этом случае каждый мгновенный импульс последовательности 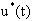преобразуется в прямоугольный длительностью Т, амплитуда которого равна площади мгновенного импульса.

Устройство, которому соответствует передаточная функция (142), называют формирующим элементом или экстраполятором нулевого порядка.

Представление цифровой части САУ в виде дискретизатора, цифрового фильтра и формирующего элемента используется для анализа и синтеза цифровых систем.

Основа автоматизированного проектирования математическое описание функционирования системы. В настоящее время преобладают и широко используются три способа математического описания автоматических систем: 1) метод передаточных функций и тесно связанные с ними частотные характеристики; 2) метод переменных состояния; З) структурно-топологические методы.

Метод передаточных функций, по существу, представляет собой применение преобразования Лапласа и частотной теории для изучения качественного поведения решений обыкновенных дифференциальных уравнений. В основе метода переменных состояния лежит представление дифференциальных уравнений в нормальной форме Коши, которое дополняется алгебраическими уравнениями, связывающими выходные переменные с переменными состояния

Математическим аппаратом метода переменных состояния (МПС) являются матричное исчисление и вычислительные методы линейной алгебры. Метод переменных состояния содействовал значительному развитию теории управления. На языке МПС выполнена большая часть работ по оптимальному управлению, фильтрации, оцениванию. В настоящее время в теории автоматических систем управления наметилось плодотворное сочетание метода переменных состояния с частотными методами. Оба способа описания взаимосвязаны и дополняют друг друга.

Топологические методы опираются на использование методов теории графов. Они получают все большее распространение, однако эффективность их применения во многом зависит от принципиальных результатов, полученных в теории графов.