 |
Лекция. Большие системы и методы их анализа
|
|
|
|
Цель: ознакомить обучающихся с понятием «большая система», методами анализа их, блочно-итерационного подхода и показать, что телекоммуникационные системы – это «большие системы».
Содержание: определение больших систем; свойства; блочно-итерационный подход к анализу БС; управление БС; математическое описание большой системы.
Понятие о больших системах, их свойства.
Большая система — управляемая система, рассматриваемая как совокупность взаимосвязанных управляемых подсистем, объединенных общей целью функционирования.
Примерами больших систем могут служить: энергосистема, включающая природные источники энергии (реки, месторождения химического или ядерного горючего, солнечную и ветровую энергию), электростанции, преобразовательные подстанции, обслуживающий персонал, линии передачи энергии, потребителей энергии; производственное предприятие, куда входят источники снабжения сырьем и энергией, персонал, технологическое оборудование, средства его ремонта, техническая документация, финансы, сбыт продукции, учет и отчетность;торговая сеть, включающая поставщиков товаров, склады, торговые точки, персонал, финансы, учет и отчетность; живой организм с его системами питания, дыхания, движения, нервной и гуморальной регуляции, восстановления разрушающихся элементов (клеток) и воспроизведения дочерних организмов.
При системном подходе, с целью изучения и совершенствования больших систем используются только такие методы, которые не игнорируют наличия тесной взаимосвязи между большим числом факторов, определяющих поведение рассматриваемой системы. Учитывается большая или меньшая неопределенность поведения системы в целом и отдельных ее частей как результат действия случайных факторов и участия в системе людей; принимается во внимание взаимовлияние системы и окружающей ее среды; учитываются изменения во времени свойств системы и внешней среды.
|
|
|
Свойства БС.
БС широко распространены в природе, технике, обществе, но, несмотря на многообразие, имеют ряд общих свойств.
Эмерджентность – свойство большой системы порождать новые свойства и качества, которых нет у ее элементов. Например, работоспособность коллектива выше суммы работоспособности его членов. Эмерджентность не дает возможности ограничиваться изучением свойств элементов БС, а требует целостного анализа всей системы.
Поведение больших систем носит вероятностный характер.
Поведение больших систем имеет единственную траекторию в прошлом и многовариантность альтернатив – в будущем.
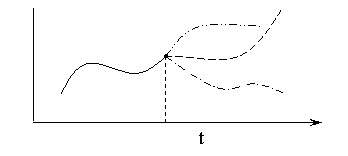
Рисунок 2.1 – Траектория поведения БС
Многоцелевое поведение БС. При управлении БС ставится и достигается несколько целей. Нередко отдельные цели конфликтны, поэтому в процессе жизненного цикла БС может происходить изменение приоритетов и установление компромиссных решений.
БС не поддаются многократному целенаправленному эксперименту, поэтому их изучение возможно только с помощью моделей (чаще всего – математических).БС не имеют четких границ и выделяются по отдельным локальным признакам.БС организованы по иерархическому признаку. Это уникальное свойство больших систем позволяет выделять в системах иерархически увязанные подсистемы, находящиеся на различных уровнях управления. Это свойство позволяет производить упрощение моделей, отображающих БС, представляя ее в виде иерархически увязанных подсистем.
При этом на каждом иерархическом уровне используются свои модели, согласованные с возможностями анализа.
Стремление уменьшать сложность моделей на каждом иерархическом уровне приводит к расчленению представлений о проектируемых (анализируемых) объектах на большое число уровней. При этом увеличивается количество и сложность задач по согласованию результатов, полученных на разных уровнях.
|
|
|
Число фактически используемых уровней зависит от объекта, традиций проектирования, возможностей математического и программного обеспечения.
Управление БС.
Управление большой системой основывается на совместном участии в процессе людей и технических средств, основу которых составляют ЭВМ и средства сбора, передачи, представления и хранения информации. Управленческий персонал в совокупности с техническими средствами образует автоматизированную систему управления, которая выполняет функции: информационно-справочные, планирования, учета, отчетности, оперативного управления, управления ресурсами и запасами. При этом выполнение формализуемых операций возлагается на ЭВМ, а принятие решений на основе неформальных методов — на руководителей.
Управление большой системой строится, как правило, в виде иерархической системы, высший орган которой управляет несколькими подразделениями низшей ступени, каждой из которых, в свою очередь, подчинены подразделения еще более низкой ступени и т.д. Такая структура управления позволяет использовать преимущества централизованных и децентрализованных систем и в значительной мере освободиться от их недостатков.
Характерная особенность современного направления развития техники управления большими системами — слияние систем управления технологическими процессами и систем организационного управления в объединенные системы управления, в которых обеспечивается наиболее эффективное и экономное использование информации и технических средств.
Блочно–иерархический подход.
Проектирование и анализ больших систем основывается на методологии блочно-иерархического подхода (БИП), представленного тремя концепциями:
- разбиение и локальная оптимизация;
- абстрагирование;
- повторяемость.
Концепция разбиения позволяет свести сложную задачу проектирования объекта к решению более простых задач с учетом взаимодействия между ними. Локальная оптимизация подразумевает улучшение параметров внутри каждой простой задачи.
|
|
|
Абстрагируемость заключается в построении формальных математических моделей, отражающих только значимые в данных условиях свойства объекта.
Повторяемость заключается в использовании существующего опыта проектирования.
Основное достоинство блочно-иерархического подхода – упрощение процесса проектирования за счет решения более простых задач на каждом иерархическом уровне.
Математическое описание большой системы.
Одна из задач исследования систем состоит в построении приближенных зависимостей между различными показателями, описывающими конкретную систему, в целях прогнозирования их состояния, имитации различных вариантов развития системы, поддержки принятия управленческих решений и т.д. Зависимость между показателями, характеризующими состояние системы, может быть представлена в виде:
y=F(x1, …, xn), (2.1)
где y, x1, …, xn - показатели, описывающие систему;
F- реальная зависимость между показателями.
Обычно для построения моделей систем, приближенно описывающих реальные зависимости, используется алгебраический многочлен некоторой степени от многих переменных.
Однако использование алгебраических многочленов в качестве моделей систем обладает определенными недостатками, следующими непосредственно из аналитического вида алгебраического многочлена.
1. Одной из характерных особенностей рассматриваемых систем является большое количество показателей, поэтому для увеличения адекватности модели необходимо увеличивать число переменных модели и степень алгебраического многочлена.
2. Другая характерная особенность рассматриваемых объектов состоит в большой изменчивости их структуры.
3. Построение моделей систем в виде алгебраических многочленов основано на предположении независимости переменных системы.
При традиционном подходе к построению приближенных зависимостей ослабить или даже “обойти” перечисленные требования невозможно.
Актуальной задачей, следовательно, является нахождение таких приемов обработки ограниченных массивов числовых данных, которые позволили бы преодолеть упрощенность модельных построений, вытекающую из традиционно используемых методов.
|
|
|
Многие трудности построения моделей систем в значительной степени связаны с аналитическим видом приближенных моделей. Поэтому возникает задача поиска новых аналитических видов приближенных зависимостей, свободных от указанных выше недостатков.
Будем использовать в качестве приближенной зависимости выражение вида:
y=a0+a1 f1 (x)+…am fm(x), (2.2)
где x=(x1, …, xn) - вектор показателей системы;
a0, a1,…, am - коэффициенты модели;
f1(x),…, fm(x) - некоторые функции.
Построение приближенной зависимости в виде (2.2) имеет значительные преимущества по сравнению с построением приближенной зависимости в виде алгебраического многочлена.
|
|
|


