 |
Лекция. Задача синтеза централизованной сети
|
|
|
|
Цель: ознакомить студентов с постановкой задачи синтеза централизованной сети, ее экономико-математической моделью и алгоритмом её решения.
Содержание: описание постановки задачи синтеза централизованной сети, формирование ее модели и методы ее реализации.
Постановка задачи.
Централизованной называется сеть, если в ней существует два иерархических уровня:
- терминалы Тi, i =1, 2,..., n, которые могут подключаться к удаленному концентратору Кj, 
, или непосредственно к ЭВМ;
- удаленные концентраторы Кj, которые соединяются с центральной ЭВМ.
Местоположение терминалов и их количество известно, известны и места возможного расположения концентраторов. Определить количество концентраторов, сеть, соединяющую терминалы с концентраторами и ЭВМ таким образом, чтобы стоимость сети была минимальна, вся информация передана от терминалов к ЭВМ – непосредственно или через концентраторы. Таким образом, должна быть решена задача синтеза сети при выполнении определенных условий – по времени задержки потоков, уровню надежности, капитальным и эксплуатационным затратам. В качестве критерия принимается стоимостная функция, а остальные требования в виде ограничений, сформулированных в том или ином виде. Например, ограничения на время задержки сформулировать сложно, но можно их представить ограничениями на поток. Например, предварительными расчетами определяются пропускные способности концентраторов, задаваемые в виде числа возможного подключения терминалов.
Итак, заданными являются:
- множества терминалов Тi и концентраторов Кj (
), ЭВМ – К 0;
- стоимости линий связи
, ;
- стоимость создания концентраторов и их пропускная способность fj, rj.
|
|
|
Определить: схему подключения терминалов к концентраторам или ЭВМ, число и расположения задействованных концентраторов, учитывая, что каждый терминал может быть соединен только с одним концентратором.
Обозначим такие соединения Тi с Кj переменной xij =1, при отсутствии связи – хi =0.
Будем называть концентратор Кj открытым, если он используется, и закрытым – в противном случае. Эта ситуация отражается переменной yj:
Очевидно, что
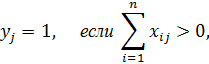
(8.1)
Тогда целевая функция стоимости запишется в виде:
(8.2)
Минимизацию целевой функции необходимо выполнить с учетом ограничений
(8.3)
(8.4)
Каждый терминал должен быть подключен либо к ЭВМ (j =0), либо к одному из концентраторов.
Второе ограничение связано с заданной возможностью подключения к концентратору ограниченного числа терминалов.
Задача представлена целочисленной (ноль-единичной) моделью линейного программирования.
Для данной модели разработано большое количество приближенных методов, т.к. получение точного решения весьма трудоемко.
Алгоритм метода добавления.
Алгоритм основан на идее последовательного улучшения плана и представляет итерационный процесс.
Шаг 0. Первоначально план прикрепления терминалов представлен множеством
,
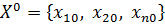т.е. все терминалы прикреплены к ЭВМ. Очевидно, что это самое дорогое решение
Итерация 1.
Действия этой итерации оценивают решения открытия одного концентратора (сначала К 1, затем К 2,...), при этом к нему должны быть присоединены те терминалы, для которых такое присоединение даст наибольший эффект, который возникает за счет уменьшения стоимости линий связи. Итерация состоит из числа шагов, равного числу концентраторов.
Шаг 1. Откроем К 1. Эффект от изменения присоединения Тi, к К 1 вместо К 0определим по формуле
. (8.5)
Очевидно, что присоединить к К 1, целесообразно только те Тi, для которых подсчитанные разности (8.5) будут положительными. Однако число таких присоединяемых Тi ограничено 
. Подсчитаем эффект, учитывая затраты f 1 на создание концентратора К 1.
|
|
|
.
(включены только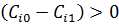 
, число их меньше ).
Аналогичных шагов будет m (по числу концентраторов).
Шаг 
. Определяются наименьшие затраты
.
Следовательно, откроем концентратор Кj, присоединив к нему 
.
Итерация 2.
Считая открытым концентратор Кj, будем открывать по очереди еще по одному концентратору.
Шаг 1. Откроем К 1, при открытом Кj оценим:
,
(8.6)
Выбираются , наибольших разностей (8.6) и подсчитываются затраты
.
Шагов будет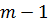 
(по числу закрытых еще концентраторов).
Шаг m. Определяется наименьшее значение функции
.
Итерация 3.
Анализируется возможность открытия третьего концентратора при уже открытых двух.
Последняя итерация состоит в открытии всех концентраторов одновременно.
Применение алгоритма метода добавления.
Проиллюстрируем описанный алгоритм примером. Пусть необходимо построить оптимальную сеть, состоящую из ЭВМ, шести терминалов и нескольких концентраторов.
Исходные данные приведены в матрице 
, векторах 
и 
.
Таблица 1 – Матрица данных
| K 0 | K 1 | K 2 | K 3 | K 4 | ||
| T 1 | 
| |||||
| T 2 | 
| |||||
| T 3 | 
| |||||
| T 4 | 
| |||||
| T5 | 
| |||||
| T 6 |
Шаг 0. Посчитаем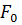 
по формуле 
.
.
Итерация 1.
Шаг 1.Открываем 
. Подсчитаем разность стоимости подключения терминала к ЭВМ или .
,
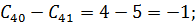
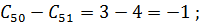
Выберем 
наибольших разностей и определим новое значение целевой функции.
.
Шаг 2.Открываем 
:
.
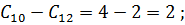
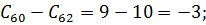
Шаг 3. Открываем 
:
Шаг 4. Открываем 
:
,
.
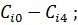
Рисунок 8.1 – Прикрепление терминалов после первой итерации
Итерация 2.
Шаг 1. При открытом 
открываем 
:
Шаг 2. При открытом 
открываем :
Шаг 3. При открытом открываем 
:
=19,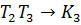 
Прикрепление терминалов показано на рисунке 8.2.
Рисунок 8.2 – Прикрепление терминалов после второй итерации
Итерация 3.
Шаг 1. При открытых и открываем :
;
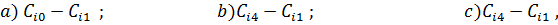
Шаг 2. При открытых и открываем :
Уменьшение целевой функции показывает целесообразность открытия концентратора 
(см. рисунок 8.3).
|
|
|
Рисунок 8.3 – Прикрепление терминалов после третьей итерации
Итерация 4. Проверим целесообразность открытия при открытых 
, и :
Отсутствие положительных разностей свидетельствует о нецелесообразности открытия , следовательно, на рисунке 8.3 приведен оптимальный граф с целевой функцией 
|
|
|
