 |
Лекция. Задача синтеза транспортной сети
|
|
|
|
Под транспортной сетью будем понимать сеть, имеющую вершину-источник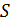 
, производящую информацию с интенсивнстью 
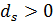, вершину-сток 
, принимающую информацию 
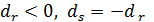и некоторое множество вершин 
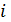– перевалочных пунктов 
. Все вершины связаны сетью, причем емкость сети заведомо больше величины перемещаемого потока. Сеть интерпретируем графом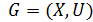 
.
Каждой дуге сети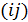 
поставлены в соответствие три характеристики:
- 
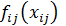– функция стоимости;
- 
– пропускная способность;
- 
– величина перемещаемого потока.
Задача состоит в построении такой сети, которая обеспечит перемещение всего потока из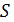 
в 
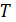с минимальной стоимостью.
Функция стоимости 
представляет собой затраты на создание и перемещение потока, т.е.
,
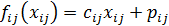где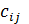 
– себестоимость транспортирования;
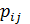– стоимость создания ребра 
.
Для выполнения этих условий вводится специальная функция
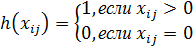
и функция стоимости принимает вид
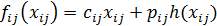. (7.1)
На величины потоков 
накладываются ограничения:
- поток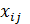 
по ребру 
не может превышать величину пропускной способности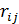 
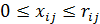; (7.2)
- сумма исходящих из 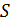потоков должна равняться 
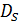, а входящих в 
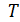– равняться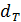 
(7.3)
- сумма входящих в вершину i потоков равна сумме выходящих
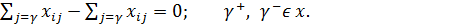(7.4)
Задача построения сети для перемещения всего потока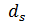 
в с минимальными затратами может быть представлена моделью математического программирования.
Определить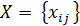 
, удовлетворяющие условиям
(7.5)
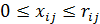, (7.6)
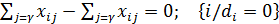, (7.7)
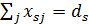, (7.8)
, (7.9)
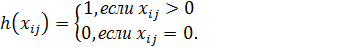(7.10)
Построенная модель относится классу сетевых задач с фиксированными доплатами, не имеющих в настоящее время точных методов решения.
Воспользуемся приближенным итерационным алгоритмом [7], состоящим из последовательности следующих шагов.
Шаг 0. Произвести первоначальное распределение потока, удовлетворяющее ограничениям (7.6 – 7.9).
|
|
|
Шаг 1. Построить дерево графа, включая в него в первую очередь основные дуги (т.е. дуги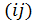 
, на которых 
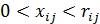). Если таковых меньше, чем дуг дерева (
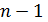где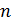 
– число вершин графа), то включаются дуги с нулевым (
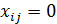) или насыщенным (
) потоком.
Шаг 2. Для каждой хорды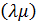 
строится цикл из дуг дерева. Направление обхода цикла определяется из следующих условий:
1) если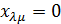 
, то поток на дуге 
можно только увеличить, и направление обхода цикла совпадает с направлением дуги 
;
2) если 
, то поток на ней можно только уменьшить, и направление обхода будет противоположно дуге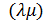 
.
Обозначим совокупность дуг цикла, направление которых совпадают с направлением обхода, положительной полуцепью 
, в противном случае – 
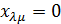. Например, если , то
,
.
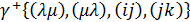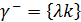На дугах положительной полуцепи возможно увеличение потока до пропускной способности, т.е.
,
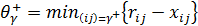а на дугах отрицательной – уменьшение потока до нуля, т.е.
.
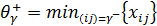Общее изменение потока в цикле
.
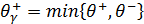Шаг 3. Величина нового потока в цикле определяется соотношением
.
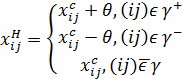Шаг 4. Проверяется целесообразность изменения потока. Изменение потока в цикле целесообразно, если стоимостная функция в цикле уменьшается, т.е. подсчитывается
,
.
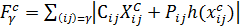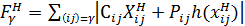Если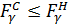 
, поток не меняется, проверяется следующий цикл (шаг 2).
Если 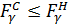, поток 
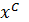заменяется на 
, алгоритм продолжается с шага 1. Расчеты закончены, если ни для одной хорды не произведено уменьшения целевой функции.
В случае, если функции 
– линейны, то проверку целесообразности изменения потока в цикле можно произвести по условиям оптимальности, аналогичным методу потенциалов.
После построения дерева подсчитываются потенциалы вершин.
.
Распределение оптимально, если в каждом цикле 
, построенном на дугах дерева добавлением одной дуги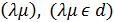 
, выполняются условия:
,
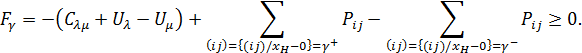
Если эти условия выполнены для всех циклов, значит, задача решена. В противном случае производится перераспределение потока и построение нового дерева.
|
|
|
|
|
|
