 |
Двухконтурный параметрический усилитель
|
|
|
|
Рис. 65. Схема двухконтурного параметрического усилителя с генератором накачки и нелинейной ёмкостью.
|
Рассмотрим конденсатор с переменной ёмкостью
,
меняющейся под действием напряжения накачки uн (t) = Uн cos(wнt). Пусть к этому конденсатору приложено переменное напряжение uС (t) = U 1cos(w 1 t + j), тогда емкостной ток составит
.
Таким образом, в спектре тока имеются компоненты с частотами w 1, wн + w 1 и wн - w 1. Эти частоты можно выделить с помощью достаточно высокодобротных контуров, настроенных на частоты w 1 и w 2 = wн ± w 1 и связанных общей нелинейной ёмкостью (рис. 65).
Полное сопротивление потерь в первом контуре будет R 1 = R '1|| Ri (где Ri - внутреннее сопротивление источника сигнала). Пусть этот контур настроен на частоту близкую к частоте усиливаемого сигнала, т. е. n 1» w 1. Соответственно, второй контур L 2 C 2 R 2 настроен на частоту w 2 = wн ± w 1 (n 2» w 2). Рассмотрим случай, когда парциальные частоты n 1 и n 2 контуров далеки друг от друга так, что связанность мала. В этом случае нормальные частоты близки к парциальным (сдвиг между парциальной и соответствующей нормальной частотами небольшой и мы можем считать, что он лежит в полосе пропускания контуров, т. е. каждый контур резонирует на своей собственной частоте). Таким образом, свою частоту контур резко усилит, остальные ослабит.
При достаточно высокой добротности контуров сопротивления каждого контура для частот, далёких от его парциальной частоты, практически равны нулю. Таким образом, контур является активной нагрузкой лишь в небольшой области частот вблизи своей парциальной частоты. В рассматриваемой нами схеме в основном контуре активная мощность может выделяться только на частоте w 1, а в дополнительном - на одной из частот w 2 = wн ± w 1. Таким образом, раз мы в каждом контуре можем следить только за одной частотой, то для этих частот запишем уравнения гармонического баланса
|
|
|
| (7.20) |
Пусть в качестве нелинейной ёмкости взят варикап. Тогда, как известно,
.
Поскольку uC = u 1 + uн - u 2, тогда в рамках гармонического баланса мы должны положить uн = Aн cos(wнt), u 1 = A 1cos(w 1 t + y 1), u 2 = A 2cos(w 2 t + y 2) (фазы y 1 и y 2 отсчитаны от напряжения накачки). Подставляя эти выражения в выражение для заряда, получим соотношения для составляющих заряда на ёмкости C на частотах w 1 и w 2:
,
.
Здесь (как и далее) верхний знак соответствует случаю w 2 = wн + w 1, а нижний - w 2 = wн - w 1.
В этом случае уравнение гармонического баланса (7.20) при воздействии гармонического сигнала i 1 = I 1cos(w 1 t + j) принимает вид:
 ,
| (7.21) |
 .
| (7.22) |
Немного упростим эти выражения, введя парциальные частоты n 1 и n 2, расстройки x 1 и x 2, добротности Q 1 и Q 2 контуров усилителя:
, 
; 
, 
;
, 
.
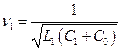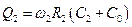Тогда в этих обозначениях уравнение (7.21) примет вид
.
Полученное соотношение должно выполняться в любой момент времени, поэтому в нём следует приравнять в правой и левой частях коэффициенты при cos(w 1 t + y 1) и sin(w 1 t + y 1). Положим в правой части j = y 1 + (j - y 1); ± y 2 = y 1 + (± y 2 - y 1), тогда после простых тригонометрических преобразований правой части, получим
 ,
| (7.23) |
 .
| (7.24) |
Аналогично из (7.22) получаем условие баланса
 ,
| (7.25) |
 .
| (7.26) |
Возведём в квадрат (7.25) и (7.26) и сложим, тогда можно получить
 .
| (7.27) |
Выразим cos(± y 2 - y 1) и sin(± y 2 - y 1) из (7.25) и (7.26) и подставим в (7.23) и (7.24):
,
.
Возведём левые и правые части этих соотношений в квадрат и сложим, а затем вместо A 2 подставим его выражение из (7.27). В результате чего получается выражение для амплитуды колебаний в первом контуре в зависимости от параметров усилителя:
 .
| (7.28) |
Напомним, что верхний знак соответствует случаю w 2 = wн + w 1, а нижний - w 2 = wн - w 1. Полученное выражение показывает, что амплитуда параметрического усилителя с низкочастотной накачкой (wн = w 2 - w 1) существенно отличается от амплитуды усилителя с высокочастотной накачкой (wн = w 2 + w 1). Рассмотрим теперь отдельно каждый из этих случаев.
|
|
|
В первом случае (при преобразовании вверх) точный максимальный сигнал будет достигнут в результате точной настройки контуров, т. е. x 1 = x 2 = 0. В этом случае амплитуды колебаний в первом и втором контурах:
 ,  .
| (7.29) | |
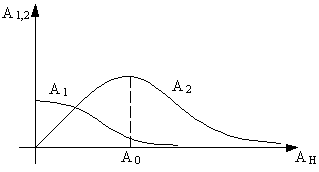Рис. 66. Зависимость амплитуд A 1 и A 2 от амплитуды накачки Aн при точной настройке контуров усилителя.
| На рис. 66 изображена зависимость A 1 и А 2 от Ан при точной настройке контуров усилителя. Из рисунка видно, что амплитуда колебаний в первом контуре монотонно уменьшается по мере увеличения амплитуды накачки. Таким образом, в этом случае усиления сигнала в первом контуре не происходит. Однако, амплитуда колебаний во втором контуре, пропорциональная амплитуде входного сигнала при А н < A 0 растёт с ростом Ан. Поэтому в системе возможно усиление с преобразованием частоты вверх, если в качестве | |
выходного сигнала использовать колебания во втором контуре усилителя. Такой усилитель является нерегенеративным параметрическим усилителем с преобразованием частоты вверх. Определим коэффициент его усиления по мощности. Под коэффициентом усиления по мощности будем понимать отношение мощности на выходе усилителя к мощности входного сигнала, выделяемой на согласованной нагрузке. Если потери первого контура достаточно малы и Ri << R '1, то R 1» R i и источник входного сигнала i 1 отдаёт в согласованную нагрузку мощность
.
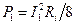Максимальная мощность на выходе усилителя:
.
Тогда коэффициент усиления по мощности нерегенеративного двухконтурного параметрического усилителя равен отношению
 ,
| (7.30) |
Поясним физический смысл этого соотношения. Вспомним квантовую теорию. Мощность на входе равна 
, где n 1 число квантов энергии на входе. Мощность на выходе аналогично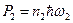 
, тогда по определению коэффициента усиления по мощности, получим
.
Сравнивая это соотношение с (7.30), мы получаем, что число квантов на выходе системы не может превышать число квантов на входе, т. е. n 1 = n 2. Таким образом, увеличение по мощности связано только с увеличением частоты квантов, а не их числа, поэтому шумы такого усилителя минимальны и он довольно устойчив.
|
|
|
Усилитель же с преобразованием частоты вниз (w 2 = wн - w 1) является обычным регенеративным усилителем и не даёт никаких преимуществ по сравнению с регенеративным режимом одноконтурного усилителя.
|
|
|
