Тема 2. Классификация измерений основные этапы измерений. Контроль гладких цилиндрических сопряжений (2часа)

План лекции:

1 Классификация измерений

2 Физические величины. Классификация физических величин

3 Основное уравнение измерений. Измерительное преобразование

4 Постулаты теории измерений

5 Испытание и контроль, предельные возможности измерений

Классификация средств измерений может проводиться по следующим критериям.

1. По характеристике точности измерения делятся на равноточные и неравноточные.

Равноточными измерениями физической величины называется ряд измерений некоторой величины, сделанных при помощи средств измерений (СИ), обладающих одинаковой точностью, в идентичных исходных условиях.

Неравноточньми измерениями физической величины на зывается ряд измерений некоторой величины, сделанных при помощи средств измерения, обладающих разной точ­ностью, и (или) в различныхисходных условиях.

2. По количеству измерений измерения делятся на однократные имногократные.

Однократное измерение — это измерение одной величины, сделанное один раз. Однократные измерения на практике имеют большую погрешность, в связи с этим рекомендуется для уменьшения погрешности выполнять минимум три раза измерения такого типа, а в качестве результата брать их сред­нее арифметическое.

Многократные измерения — это измерение одной или нескольких величин, выполненное четыре и более раз. Мно­гократное измерение представляет собой ряд однократных из­мерений. Минимальное число измерений, при котором изме­рение может считаться многократным, — четыре. Результатом многократного измерения является среднее арифметическое результатов всех проведенных измерений. При многократных измерениях снижается погрешность.

3. По типу изменения величины измерения делятся на ста­тические и динамические.

Статические измерения — это измерения постоянной, неизменной физической величины. Примером такой постоянной во времени физической величины может послужить дли­на земельного участка.

Динамические измерения — это измерения изменяющейся, непостоянной физической величины.

4. По предназначению измерения делятся на технические и метрологические.

Технические измерения — это измерения, выполняемые техническими средствами измерений.

Метрологические измерения — это измерения, выполняе­мые с использованием эталонов.

5. По способу представления результата измерения делятся на абсолютные и относительные.

Абсолютные измерения — это измерения, которые выпол­няются посредством прямого, непосредственного измерения основной величины и (или) применения физической кон­станты.

Относительные измерения — это измерения, при которых вычисляется отношение однородных величин, причем числи­тель является сравниваемой величиной, а знаменатель — ба­зой сравнения (единицей). Результат измерения будет зави­сеть от того, какая величина принимается за базу сравнения.

6. По методам получения результатов измерения делятся на прямые, косвенные, совокупные и совместные.

Прямые измерения — это измерения, выполняемые при помощи мер, т.е. измеряемая величина сопоставляется не­посредственно с ее мерой. Примером прямых измерений яв­ляется измерение величины угла (мера — транспортир).

Косвенные измерения — это измерения, при которых зна­чение измеряемой величины вычисляется при помощи зна­чений, полученных посредством прямых измерений, и неко­торой известной зависимости между данными значениями И измеряемой величиной.

Совокупные измерения — это измерения, результатом ко­торых является решение некоторой системы уравнений, которая с оставлена из уравнений, полученных вследствие из­мерения возможных сочетаний измеряемых величин.

Совместные измерения — это измерения, в ходе которых ичмеряется минимум две неоднородные физические величи­ны с целью установления существующей между ними зави­симости.

Все объекты окружающего мира характеризуются своими свойствами. Свойство – это философская категория, выражающая такую сторону объекта (явления, процесса), которая обуславливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним. Свойство – категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина — это свойство чего-либо, которое может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной. Идеальные величины главным образом относятся к математике, и являются обобщением (моделью) конкретных реальных понятий. Они вычисляются тем или иным способом.

Многие свойства, помимо отношения эквивалентности, проявляют себя и в отношении наличия у них количественной ординаты свойства — интенсивности. При расчленении объекта такие свойства обычно не изменяются и называются интенсивными величинами. Путем сравнения интенсивных величин можно определить их соотношение, упорядочить по интенсивности данного свойства. При сравнении интенсивных величин выявляется отношение порядка (больше, меньше или равно), т.е. определяется соотношение между величинами. Примерами интенсивных величин являются твердость материала, запах и др. Интенсивные величины могут быть обнаружены, классифицированы по интенсивности, подвергнуты контролю, количественно оценены монотонно возрастающими или убывающими числами. На основании понятия "интенсивная величина" вводятся понятия физической величины и ее размера. Размер физической величины — количественное содержание в данном объекте свойства, соответствующего понятию физической величины.

Интенсивные величины отображаются путем количественного, главным образом экспертного, оценивания, при котором свойства с большим размером отображаются большим числом, чем свойства с меньшим размером. Интенсивные величины оцениваются при помощи шкал порядка и интервалов, рассмотренных далее.

Объекты, характеризующиеся интенсивными величинами, могут быть подвергнуты контролю. Контроль — это процедура установления соответствия между состоянием объекта и нормой. Для реализации процедуры простейшего однопараметрового контроля свойства X необходимы образцовые объекты, которые характеризуют параметры, равные соответственно нижней Х_н и верхней Х_в границам нормы, и устройство сравнения. Результат контроля Q определяется следующим уравнением: ниже нормы (X<Х_н); норма (X>Х_н и X<Х_в); выше нормы (X>Х_в).

Если физическая величина проявляется в отношениях эквивалентности, порядка и аддитивности, то она может быть: обнаружена, классифицирована, проконтролирована и измерена. Эти величины, называемые экстенсивными, характеризуют обычно физические вещественные или энергетические свойства объекта, например массу тела, электрическое сопротивление проводника и др. При измерении экстенсивной величины несчетное множество ее размеров отображается на счетное подмножество в виде совокупности чисел Q, которое также должно удовлетворять отношениям эквивалентности, порядка и аддитивности. Числа Q — это результаты измерений, они могут быть использованы для любых математических операций. Совокупность таких чисел Q должна обладать следующими свойствами:

- для проявления в отношении эквивалентности совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это наименование является единицей физическая величина или ее доли. Единица физической величины [Q] — это физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице. Она применяется для количественного выражения однородных физических величин.

- для проявления в отношениях эквивалентности и порядка число q₁, отображающее большую по размеру величину Q₁>Q₂ выбирается большим, чем число q₂, отображающее меньшую по размеру величину Q₂. При этом в обоих случаях используется одна единица физической величины. Для выполнения данного условия в качестве искомой совокупности q₁,…, q_n выбирают упорядоченное множество действительных чисел с естественным отношением порядка.

- для проявления в отношениях эквивалентности, порядка и аддитивности отвлеченное число, равное оценке суммарной измеряемой величины Q, возникающей в результате сложения составляющих однородных величин Q_i, должно быть равно сумме числовых оценок qi этих составляющих. Сумма именованных чисел Q_i, отражающих составляющие, должна быть равна именованному числу Q, отражающему суммарную величину:

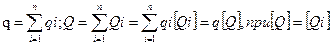(2.1)

Если реализовано условие [Q] = [Q_i], т. е. имеет место равенство размеров единиц у всех именованных чисел, отражающих суммарную величину Q и ее составляющие Q_i, то в этом случае вводятся следующие понятия:

- значение физической величины Q - это оценка ее размера в виде некоторого числа принятых для нее единиц;

- числовое значение физической величины, q — отвлеченное число, выражающее отношение значения величины к соответствующей единице данной физической величины.

Уравнение Q = q[Q] называют основным уравнением измерения. Суть простейшего измерения состоит в сравнении размера физической величины Q с размерами выходной величины регулируемой многозначной меры q[Q]. В результате сравнения устанавливают, что q[Q]<Q<(q+1)[Q]. Отсюда следует, что q = Int(Q/[Q]), где Int(X) — функция, выделяющая целую часть числа X.

Условием реализации процедуры элементарного прямого измерения является выполнение следующих операций:

- воспроизведение физической величины заданного размера q[Q];

- сравнение измеряемой физической величины Q с воспроизводимой мерой величиной q[Q].

Таким образом, на основе использования общих постулатов эквивалентности, порядка и аддитивности получено понятие прямого измерения, которое может быть сформулировано следующим образом: измерение — познавательный процесс, заключающийся в сравнении путем физического эксперимента данной физической величины с известной физической величиной, принятой за единицу измерения.

Как и любая другая наука, теория измерения строится на основе ряда основополагающих постулатов, описывающих ее исходные аксиомы. Построению и исследованию этих аксиом—постулатов посвящено большое число научных исследований.

Следует отметить, что любая попытка сформулировать исходные положения (постулаты) теории измерений встречает принципиальные затруднения. Это связано с тем, что, с одной стороны, постулаты должны представлять собой объективные утверждения, а с другой — предметом метрологии являются измерения, т.е. вид деятельности людей, предпринимаемой ими для достижения субъективных целей. Следовательно, необходимо сформулировать объективные утверждения, которые бы служили фундаментом научной дисциплины, имеющей существенный субъективный элемент. Первым постулатом метрологии является постулат a: в рамках принятой модели объекта исследования существует определенная измеряемая физическая величина и ее истинное значение. Если, например, считать, что деталь представляет собой цилиндр (модель — цилиндр), то она имеет диаметр, который может быть измерен. Если же деталь нельзя считать цилиндрической, например ее сечение представляет собой эллипс, то измерять ее диаметр бессмысленно, поскольку измеренное значение не несет полезной информации о детали. И, следовательно, в рамках новой модели диаметр не существует. Измеряемая величина существует лишь в рамках принятой модели, т.е. имеет смысл только до тех пор, пока модель признается адекватной объекту. Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели, то из постулата, а вытекает следствие a₁: для данной физической величины объекта измерения существует множество измеряемых величин и соответственно их истинных значений.

Итак, из первого постулата метрологии следует, что измеряемому свойству объекта измерений должен соответствовать некоторый параметр его модели. Данная модель в течение времени, необходимого для измерения, должна позволять считать этот ее параметр неизменным. В противном случае измерения не могут быть проведены. Указанный факт описывается постулатом b: истинное значение измеряемой величины постоянно.

Выделив постоянный параметр модели, можно перейти к измерению соответствующей величины. Для переменной физической величины необходимо выделить или выбрать некоторый постоянный параметр и измерить его. В общем случае такой постоянный параметр вводится с помощью некоторого функционала. Примером таких постоянных параметров переменных во времени сигналов, вводимых посредством функционалов, являются средневыпрямленные или среднеквадратические значения. Данный аспект отражается в следствии b1: для измерения переменной физической величины необходимо определить ее постоянный параметр — измеряемую величину.

Измерения, основанные на использовании органов чувств человека (осязания, обоняния, зрения, слуха и вкуса), называется органолептическими. Измерение времени, например, или гравитации (космонавтами) основываются на ощущениях. Еще менее совершенные измерения по шкале порядка строятся на впечатлениях.

Измерения, основанные на интуиции, называются эвристическими.

Измерения, выполняемые с помощью специальных технических средств, называются инструментальными. Среди них могут быть автоматизированные и автоматические. При автоматизированных измерениях роль человека полностью не исключена (проводить съем данных с отчетного устройства измерительного прибора или цифрового табло). Автоматические измерения выполняются без участия человека. Результат их представляется в форме документа и является совершенно объективным.

Индикаторами называются технические устройства, предназначенные для обнаружения физических свойств.

Средствами измерений называются, все технические средства, используемые при измерениях и имеющие нормированные метрологические характеристики.

Вещественные меры предназначены для воспроизведения физической величины заданного размера, который характеризуется так называемым номинальным размером.

Измерительные преобразователи – это средства измерений, вырабатывающие сигналы измерительной информации в форме, удобной для дальнейшего преобразования, передачи, хранения, обработки, но, как правило, недоступной для непосредственного восприятия наблюдателем.

Под единством измерений понимают такое состояние, при котором результаты выражены в узаконенных единицах, а точность измерений документирована.

Метрологическими характеристиками средств измерений называются такие их технические характеристики, которые влияют на результаты и точность измерений.

Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины — это упорядоченная последовательность значений физической величины, принятая по соглашению на основании результатов точных измерений.

В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.

Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности, Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами физической величины. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.

Шкала порядка (шкала рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства. Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк — 1; гипс — 2; кальций — 3; флюорит — 4; апатит — 5; ортоклаз — 6; кварц — 7; топаз — 8; корунд — 9; алмаз — 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) — не остается, то твердость испытуемого материала составляет более 6, но менее 7. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.

Шкала интервалов (шкала разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало — нулевую точку. К таким шкалам относятся летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов. Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Q₀ и Q₁ величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал — основным интервалом (Q₁-Q₀).

Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Их примерами являются шкала массы (второго рода), термодинамической температуры (первого рода). В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения шкала отношений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении физической величины. Шкалы отношений — самые совершенные.

Абсолютные шкалы. Некоторые авторы используют понятие абсолютных шкал, под которыми понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначно с определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Отметим, что шкалы наименований и порядка называют неметрическими (копцептуалъными), а шкалы интервалов и отношений — метрическими (материальными). Абсолютные и метрические шкалы относятся к разряду линейных. Практическая реализация шкал измерений осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.

 

Контрольные вопросы:

1 Дайте определение физической величины. Приведите примеры величин, принадлежащих к различным группам физических процессов.

2 Что такое экстенсивные и интенсивные физические величины? В чем их сходство и различие? Приведите примеры физических величин каждого вида.

3 Что такое шкала физической величины? Приведите примеры различных шкал физических величин.

4 Назовите основные операции процедуры измерения. Расскажите, как они реализуются при измерении размера детали штангенциркулем.

5 Приведите примеры измерительных преобразователей, многозначных мер и устройств сравнения, используемых в известных вам средствах измерений.

6 Что такое средство измерений? Приведите примеры средств измерений различных физических величин.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: