 |
Часть 2 Фундаментальные алгоритмы 5 глава
|
|
|
|
Раздел 6.2
Упражнение 6.5 Покажите, что в каждом вычислении древовидного алгоритма (Алгоритм 6.3) решение принимают ровно два процесса.
Упражнение 6.6 Используя эхо-алгоритм (Алгоритм 6.5), составьте алгоритм, который вычисляет префиксную схему маркировки (см. Подраздел 4.4.3) для произвольной сети с использованием 2|E| сообщений и O(N) единиц времени.
Можете ли вы привести алгоритм, вычисляющий схему маркировки за время O(D)? (D - диаметр сети.)
Упражнение 6.7 Покажите, что соотношение в Лемме 6.19 выполняется, если сообщение потерялось в канале pq, но не выполняется, если сообщения могут дублироваться. Какой шаг доказательства не действует, если сообщения могут дублироваться?
Упражнение 6.8 Примените построение в Теореме 6.12 к фазовому алгоритму так, чтобы получить алгоритм, вычисляющий максимум по целочисленным входам всех процессов.
Каковы сложность сообщений, временная и битовая сложность вашего алгоритма?
Упражнение 6.9 Предположим, вы хотите использовать волновой алгоритм в сети, где может произойти дублирование сообщений.
(1) Какие изменения должны быть сделаны в эхо-алгоритме?
(2) Какие изменения должны быть сделаны в алгоритме Финна?
Раздел 6.3
Упражнение 6.10 Полный двудольный граф - это граф G = (V,E), где V = V1 È V2 при V1 Ç V2 = Æ и E = V1 ´ V2.
Приведите алгоритм 2 x- обхода для полных двудольных сетей.
Упражнение 6.11 Докажите или опровергните: Обход гиперкуба без чувства направления требует Q(N logN) сообщений.
Раздел 6.4
Упражнение 6.12 Приведите пример вычисления алгоритма Тарри, в котором в результате получается не DFS- дерево.
Упражнение 6.13 Составьте алгоритм, который вычисляет интервальные схемы маркировки поиска в глубину (см. Подраздел 4.4.2) для произвольных связных сетей.
|
|
|
Может ли это быть сделано за O(N) единиц времени? Может ли это быть сделано с использованием O(N) сообщений?
Упражнение 6.14 Предположим, что алгоритм поиска в глубину со знанием соседей используется в системе, где каждый процесс знает не только идентификаторы своих соседей, но и множество идентификаторов всех процессов (P). Покажите, что в этом случае достаточно сообщений, состоящих из N бит.
Раздел 6.5
Упражнение 6.15 Адаптируйте эхо-алгоритм (Алгоритм 6.5) для вычисления суммы по входам всех процессов.
Упражнение 6.16 Предположим, что процессы в сетях, изображенных на Рис.6.21, имеют уникальные идентификаторы, и каждый процесс имеет целочисленный вход. Смоделируйте на обеих сетях вычисление фазового алгоритма, вычисляя множество S = {(p, jp): p Î P} и сумму по входам.
Упражнение 6.17 Какова цепочечная сложность фазового алгоритма для клик (Алгоритм 6.8)?
7 Алгоритмы выбора
В этой главе будут обсуждаться проблемы выбора, также называемого нахождением лидера. Задача выбора впервые была изложена ЛеЛанном [LeLann; LeL77], который предложил и первое решение; см. Подраздел 7.2.1. Задача начинается в конфигурации, где все процессы находятся в одинаковом состоянии, и приходит в конфигурацию, где ровно один процесс находится в состоянии лидера (leader), а все остальные - в состоянии проигравших (lost).
Выбор среди процессов нужно проводить, если должен быть выполнен централизованный алгоритм и не существует заранее известного кандидата на роль инициатора алгоритма. Например, в случае процедуры инициализации системы, которая должна быть выполнена в начале или после сбоя системы. Т.к. множество активных процессов может быть неизвестно заранее, невозможно назначить один процесс раз и навсегда на роль лидера.
Существует большое количество результатов о задаче выбора (как алгоритмы, так и более общие теоремы). Результаты для включения в эту главу выбирались по следующим критериям.
|
|
|
(1) Синхронные системы, анонимные процессы, и отказоустойчивые алгоритмы обсуждаются в других главах. В этой главе всегда предполагается, что процессы и каналы надежны, система полностью асинхронна, и процессы различаются уникальными идентификаторами.
(2) Мы сосредоточим внимание на результатах, касающихся сложности сообщений. Алгоритмы с улучшенной временной сложностью или результаты, предполагающие компромисс между временной сложностью и сложностью сообщений, не обсуждаются.
(3) Мы будем уделять внимание порядку величины сложности сообщений, и не будем рассматривать результаты, вносящие в сложность только постоянный множитель.
(4) Т.к. результаты Кораха и др. (Раздел 7.4) подразумевают существование O(N logN)-алгоритмов для нескольких классов сетей, алгоритм для клики с этой сложностью не будет рассматриваться отдельно.
7.1 Введение
Задача выбора требует, чтобы из конфигурации, где все процессы находятся в одинаковом состоянии, система пришла в конфигурацию, где ровно один процесс находится в особом состоянии лидер (leader), а все остальные процессы - в состоянии проигравших (lost). Процесс, находящийся в состоянии лидер в конце вычисления, называется лидером и говорят, что он выбран алгоритмом.
Определение 7.1 Алгоритм выбора - это алгоритм, удовлетворяющий следующим требованиям.
(1) Каждый процесс имеет один и тот же локальный алгоритм.
(2) Алгоритм является децентрализованным, т.е. вычисление может быть начато произвольным непустым подмножеством процессов.
(3) Алгоритм достигает заключительной конфигурации в каждом вычислении, и в каждой достижимой заключительной конфигурации существует ровно один процесс в состоянии лидера, а все остальные процессы - в состоянии проигравших.
Иногда последнее требование ослабляется и требуется только, чтобы ровно один процесс находился в состоянии лидера. В этом случае выбранный процесс знает, что он победил, но проигравшие (еще) не знают, что они проиграли. Если дан алгоритм, удовлетворяющий этим ослабленным действиям, то его можно легко расширить, добавив инициируемую лидером рассылку сообщений всем процессам, при которой все процессы информируются о результатах выбора. В некоторых алгоритмах этой главы это дополнительное оповещение опущено.
|
|
|
Во всех алгоритмах этой главы процесс p имеет переменную statep с возможными значениями leader (лидер) и lost (проигравший). Иногда мы будем предполагать, что statep имеет значение sleep (спящий), когда p еще не выполнил ни одного шага алгоритма, и значение cand (кандидат), если p вступил в вычисление, но еще не знает, победил он или проиграл. Некоторые алгоритмы используют дополнительные состояния, такие как active, passive и др., которые будут указаны в самом алгоритме.
7.1.1 Предположения, используемые в этой главе
Рассмотрим предположения, при которых задача выбора изучалась в этой главе.
(1) Система полностью асинхронна. Предполагается, что процессам недоступны общие часы, и что время передачи сообщения может быть произвольно долгим или коротким.
Оказывается, что предположение о синхронной передаче сообщений (т.е. когда отправление и получение сообщения считается единой передачей) незначительно влияет на результаты, полученные для задачи выбора. Читатель может сам убедиться, что алгоритмы, данные в этой главе, могут применяться в системах с синхронной передачей сообщений, и что полученные нижние границы также применимы в этом случае.
Предположение о существовании глобального времени, также как и предположение о том, что процессам доступно реальное время и что задержка сообщений ограничена, имеют важное влияние на решения задачи выбора.
(2) Каждый процесс идентифицируется уникальным именем, своим идентификатором, который известен процессу изначально. Для простоты предполагается, что идентификатор процесса p - просто p. Идентификаторы извлекаются из совершенно упорядоченного множества P, т.е. для идентификаторов определено отношение £. Количество бит, представляющих идентификатор, равно w.
Важность уникальных идентификаторов в задаче выбора состоит в том, что они могут использоваться не только для адресации сообщений, но и для нарушения симметрии между процессами. При разработке алгоритма выбора можно, например, потребовать, что процесс с наименьшим (или наоборот, с наибольшим) идентификатором должен победить. Тогда задача состоит в поиске наименьшего идентификатора с помощью децентрализованного алгоритма. В этом случае задачу выбора называют задачей поиска экстремума.
|
|
|
Хотя некоторые из алгоритмов, обсуждаемых в этой главе, изначально были изложены для нахождения наибольшего процесса, мы излагаем большинство алгоритмов для выбора наименьшего процесса. Во всех случаях алгоритм для выбора наибольшего процесса можно получить, изменив порядок сравнения идентификаторов.
(3) Некоторые результаты этой главы относятся к алгоритмам сравнения. Алгоритмы сравнения - это алгоритмы, которые используют сравнение как единственную операцию над идентификаторами. Как мы увидим, все алгоритмы, представленные в этой главе, являются алгоритмами сравнения. Всякий раз, когда дается оценка нижней границы, мы явно отмечаем, касается ли она алгоритмов сравнения.
Было показано (например, Бодлендером [Bodlaender, Bod91b] для случая кольцевых сетей), что в асинхронных сетях произвольные алгоритмы не достигают лучшей сложности, чем алгоритмы сравнения. Это не так в случае синхронных систем, как будет показано в Главе 11; в этих системах произвольные алгоритмы могут достигать лучшей сложности, чем алгоритмы сравнения.
(4) Каждое сообщение может содержать O(w) бит. Каждое сообщение может содержать не более постоянного числа идентификаторов процессов. Это предположение сделано для того, чтобы позволить справедливое сравнение сложности сообщений различных алгоритмов.
7.1.2 Выбор и волны
Уже было замечено, что идентификаторы процессов могут использоваться для нарушения симметрии между процессами. Можно разработать алгоритм выбора так, чтобы выбирался процесс с наименьшим идентификатором. Согласно результатам в Подразделе 6.1.5, наименьший идентификатор может быть вычислен за одну волну. Это означает, что выбор можно провести, выполняя волну, в которой вычисляется наименьший идентификатор, после чего процесс с этим идентификатором становится лидером. Т.к. алгоритм выбора должен быть децентрализованным, этот принцип может быть применен только к децентрализованным волновым алгоритмам (см. Таблицу 6.19).
Выбор с помощью древовидного алгоритма. Если топология сети - дерево или доступно остовное дерево сети, выбор можно провести с помощью древовидного алгоритма (Подраздел 6.2.2). В древовидном алгоритме требуется, чтобы хотя бы все листья были инициаторами алгоритма. Чтобы получить развитие алгоритма в случае, когда некоторые процессы также являются инициаторами, добавляется фаза wake-up. Процессы, которые хотят начать выбор, рассылают сообщение < wakeup > всем процессам. Логическая переменная ws используется, чтобы каждый процесс послал сообщения < wakeup > не более одного раза, а переменная wr используется для подсчета количества сообщений < wakeup >, полученных процессом. Когда процесс получит сообщение < wakeup > через каждый канал, он начинает выполнять Алгоритм 6.3, который расширен (как в Теореме 6.12) таким образом, чтобы вычислять наименьший идентификатор и чтобы каждый процесс принимал решение. Когда процесс принимает решение, он знает идентификатор лидера; если этот идентификатор совпадает с идентификатором процесса, он становится лидером, а если нет - проигравшим; см. Алгоритм 7.1.
|
|
|
var wsp : boolean init false;
wrp : integer init 0;
recp[q]: boolean для всех q Î Neighp init false;
vp : P init p;
statep: (sleep, leader, lost) init sleep;
begin if p - инициатор then
begin wsp:= true;
forall q Î Neighp do send < wakeup > to q
end;
while wrp < # Neighp do
begin receive < wakeup >; wrp:= wrp + 1;
if not wsp then
begin wsp:= true;
forall q Î Neighp do send < wakeup > to q
end
end;
(* Начало древовидного алгоритма *)
while # {q: Ørecp[q]} > 1 do
begin receive < tok,r> from q; recp[q]:= true;
vp:= min (vp,r)
end;
send < tok,vp> to q0 with Ørecp[q0];
receive < tok,r> from q0;
vp:= min (vp,r); (* decide с ответом vp *)
if vp = p then statep:= leader else statep:= lost;
forall q Î Neighp, q ¹ q0 do send < tok,vp> to q
End
Алгоритм 7.1 Алгоритм выборов для деревьев.
Теорема 7.2 Алгоритм 7.1 решает задачу выбора на деревьях, используя O(N) сообщений и O(D) единиц времени.
Доказательство. Когда хотя бы один процесс инициирует выполнение алгоритма, все процессы посылают сообщения < wakeup > всем своим соседям, и каждый процесс начинает выполнение древовидного алгоритма после получения сообщения < wakeup > от каждого соседа. Все процессы завершают древовидный алгоритм с одним и тем же значением v, а именно, наименьшим идентификатором процесса. Единственный процесс с этим идентификатором закончит выполнение в состоянии лидер, а все остальные процессы - в состоянии проигравший.
Через каждый канал пересылается по два сообщения < wakeup > и по два сообщения < tok,r>, откуда сложность сообщений равна 4N-4. В течение D единиц времени после того, как первый процесс начал алгоритм, каждый процесс послал сообщения < wakeup >, следовательно, в течение D+1 единиц времени каждый процесс начал волну. Легко заметить, что первое решение принимается не позднее, чем через D единиц времени после начала волны, а последнее решение принимается не позднее D единиц времени после первого, откуда полное время равно 3D+1. Более тщательный анализ показывает, что алгоритм всегда завершается за 2D единиц времени, но доказательство этого оставлено читателю; см. Упражнение 7.2.
Если порядок сообщений в канале может быть изменен (т.е. канал - не FIFO), процесс может получить сообщение < tok,r> от соседа прежде чем он получил сообщение < wakeup > от этого соседа. В этом случае сообщение < tok,r> может быть временно сохранено или обработано как сообщения < tok,r>, прибывающие позднее.
Количество сообщений может быть уменьшено с помощью двух модификаций. Во-первых, можно устроить так, чтобы не-инициатор не посылал сообщение < wakeup > процессу, от которого он получил первое сообщение < wakeup >. Во-вторых, сообщение < wakeup >, посылаемое листом, может быть объединено с сообщением < tok,r>, посылаемым этим листом. С этими изменениями количество сообщений, требуемое алгоритмом, уменьшается до 3N-4+k, где k - количество нелистовых стартеров [Tel91b, с.139].
Выбор с помощью фазового алгоритма. Фазовый алгоритм можно использовать для выбора, позволив ему вычислять наименьший идентификатор за одну волну, как в Теореме 6.12.
Теорема 7.3 С помощью фазового алгоритма (Алгоритм 6.7) можно провести выбор в произвольных сетях, используя O(D*|E|) сообщений и O(D) единиц времени.
Алгоритм Пелега [Peleg; Pel90] основан на фазовом алгоритме; он использует O(D*|E|) сообщений и O(D) времени, но не требует знания D, т.к. включает в себя вычисление диаметра.
Выбор с помощью алгоритма Финна. Алгоритм Финна (Алгоритм 6.9) не требует, чтобы диаметр сети был известен заранее. Длина O(N*|E|) сообщений, используемых в алгоритме Финна, гораздо больше, чем допускаемая предположениями в этой главе. Следовательно, каждое сообщение в алгоритме Финна должно считаться за O(N) сообщений, откуда сложность сообщений составляет O(N2|E|).
7.2 Кольцевые сети
В этом разделе рассматриваются некоторые алгоритмы выбора для однонаправленных колец. Задача выбора в контексте кольцевых сетей была впервые изложена ЛеЛанном [LeLann; LeL77], который также дал решение со сложностью сообщений O(N2). Это решение было улучшено Чангом (Chang) и Робертсом (Roberts) [CR79], которые привели алгоритм с наихудшей сложностью O(N2), но со средней сложностью только O(N logN). Решения ЛеЛанна и Чанга-Робертса обсуждаются в Подразделе 7.2.1. Вопрос о существовании алгоритма с наихудшей сложностью O(N logN) оставался открытым до 1980 г., когда такой алгоритм был приведен Hirschberg и Sinclair [HS80]. В отличие от более ранних решений, в решении Hirschberg-Sinclair требуется, чтобы каналы были двунаправленными. Предполагалось, что нижняя граница для однонаправленных колец равна W(N2), но Petersen [Pet82] и Dolev, Klawe и Rodeh [DKR82] независимо друг от друга предложили решение, составляющее O(N log N) для однонаправленного кольца. Это решение рассматривается в Подразделе 7.2.2.
Алгоритмы были дополнены соответствующими нижними границами примерно в то же время. Нижняя граница для наихудшего случая для двунаправленных колец, равная» 0.34N logN сообщений, была доказана Бодлендером [Bodlaender; Bod88]. Pachl, Korach и Rotem [PKR84] доказали нижние границы в W(N logN) для средней сложности, как для двунаправленных так и для однонаправленных колец. Их результаты по нижним границам будут рассмотрены в Подразделе 7.2.3.
7.2.1 Алгоритмы ЛеЛанна и Чанга-Робертса
В алгоритме ЛеЛанна [LeL77] каждый инициатор вычисляет список идентификаторов всех инициаторов, после чего выбирается инициатор с наименьшим идентификатором. Каждый инициатор посылает маркер, содержащий его идентификатор, по кольцу, и этот маркер передается всеми процессами. Предполагается, что каналы подчиняются дисциплине FIFO, и что инициатор должен сгенерировать свой маркер до того, как он получит маркер другого инициатора. (Когда процесс получает маркер, он после этого не инициирует алгоритм.) Когда инициатор p получает свой собственный маркер, маркеры всех инициаторов прошли через p, и p выбирается лишь в том случае, если p - наименьший среди инициаторов; см. Алгоритм 7.2.
var Listp : set of P init {p};
statep;
begin if p - инициатор then
begin statep:= cand; send < tok,p> to Nextp; receive < tok,q>;
while q ¹ p do
begin Listp:= Listp È {q};
send < tok,q> to Nextp; receive < tok,q>;
end;
if p = min (Listp) then statep:= leader
else statep:= lost
end
else repeat receive < tok,q>; send < tok,q> to Nextp;
if statep = sleep then statep:= lost
until false
End
Алгоритм 7.2 Алгоритм выбора ЛеЛанна.
Теорема 7.4 Алгоритм ЛеЛанна (Алгоритм 7.2) решает задачу выбора для колец, используя O(N2) сообщений и O(N) единиц времени.
Доказательство. Так как порядок маркеров в кольце сохраняется (из предположения о каналах FIFO), и инициатор q отправляет < tok,q> до того как получит < tok,p>, то инициатор p получает < tok,q> прежде, чем вернется < tok,p>. Отсюда следует, что каждый инициатор p заканчивается со списком Listp, совпадающим с множеством всех инициаторов, и единственным выбираемым процессом становится инициатор с наименьшим идентификатором. Всего получается не больше N маркеров и каждый делает N шагов, что приводит к сложности сообщений в O(N2). Не позднее чем через N-1 единицу времени после того, как первый инициатор отправил свой маркер, это сделали все инициаторы. Каждый инициатор получает свой маркер обратно не позднее, чем через N единиц времени с момента генерации этого маркера. Отсюда следует, что алгоритм завершается в течение 2N-1 единиц времени.
Все не-инициаторы приходят в состояние проигравший, но навсегда остаются в ожидании сообщений < tok,r>. Ожидание может быть прервано, если лидер посылает по кольцу специальный маркер, чтобы объявить об окончании выбора.
Алгоритм Чанга-Робертса [CR79] улучшает алгоритм ЛеЛанна, устраняя из кольца маркеры тех процессов, для которых очевидно, что они проиграют выборы. Т.е. инициатор p удаляет из кольца маркер < tok,q>, если q > p. Инициатор p становится проигравшим, когда получает маркер с идентификатором q < p, или лидером, когда он получает маркер с идентификатором p; см. Алгоритм 7.3.
var statep;
begin if p - инициатор then
begin statep:= cand; send < tok,p> to Nextp;
repeat receive < tok,q>;
if q = p then statep:= leader
else if q < p then
begin if statep = cand then statep:= lost;
send < tok,q> to Nextp
end
until statep = leader
end
else repeat receive < tok,q>; send < tok,q> to Nextp;
if statep = sleep then statep:= lost
until false
End
(* Только лидер завершает выполнение программы. Он передает сообщение всем процессам, чтобы сообщить им идентификатор лидера и завершить их *)
Алгоритм 7.3 Алгоритм выбора Чанга-Робертса.
Теорема 7.5 Алгоритм Чанга-Робертса (Алгоритм 7.3) решает задачу выбора для колец, используя Q(N2) сообщений в наихудшем случае и O(N) единиц времени.
Доказательство. Пусть p0 - инициатор с наименьшим идентификатором. Все процессы являются либо не-инициаторами, либо инициаторами с идентификаторами большими p0, поэтому все процессы передают дальше маркер < tok,p0>, отправленный p0. Следовательно, p0 получает свой маркер обратно и становится выбранным.
Не-инициаторы не могут быть выбраны, т.к. все они приходят в состояние проигравший самое позднее, когда через них передается маркер p0. Инициатор p с p > p0 не может быть выбран; p0 не передаст дальше маркер < tok,p>, поэтому p никогда не получит свой собственный маркер. Такой инициатор p приходит в состояние проигравший самое позднее, когда через него передается маркер < tok,p0>. Таким образом доказано, что алгоритм решает задачу выбора.
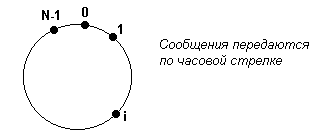
Рис.7.4 Наихудший случай для алгоритма Чанга-Робертса.
Всего используется не более N различных маркеров и каждый маркер делает не более N переходов, что подтверждает границу сложности сообщений O(N2). Чтобы показать, что в самом деле можно использовать W(N2) сообщений, рассмотрим начальную конфигурацию, где все идентификаторы расположены в возрастающем порядке вдоль кольца (см. Рис. 7.4) и каждый процесс является инициатором. Маркер каждого процесса удаляется из кольца процессом 0, таким образом маркер процесса i совершает N-i переходов, откуда следует, что количество пересылок сообщений равно.
Алгоритм Чанга-Робертса не улучшает алгоритм ЛеЛанна в отношении временной сложности или наихудшего случая сложности сообщений. Улучшение касается только среднего случая, где усреднение ведется по всевозможным расположениям идентификаторов вдоль кольца.
Теорема 7.6 Алгоритм Чанга-Робертса в среднем случае, когда все процессы являются инициаторами, требует только O(N logN) пересылок сообщений.
Доказательство. (Это доказательство основано на предложении Friedemann Mattern.)
Предположив, что все процессы являются инициаторами, вычислим среднее количество пересылок маркера по всем круговым расположениям N различных идентификаторов. Рассмотрим фиксированное множество из N идентификаторов, и пусть s будет наименьшим идентификатором. Существует (N-1)! различных круговых расположений идентификаторов; в данном круговом расположении пусть pi - идентификатор, находящийся за i шагов до s; см. Рис. 7.5.
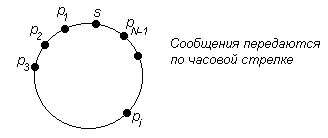
Рис.7.5 Расположение идентификаторов на кольце.
Чтобы вычислить суммарное количество пересылок маркера по всем расположениям, вычислим сначала суммарное количество пересылок маркера < tok,pi> по всем расположениям, а потом просуммируем по i. Маркер < tok,s> при любом расположении передается N раз, следовательно, он пересылается всего N(N-1)! раз. Маркер < tok,pi> передается не более i раз, так как он будет удален из кольца, если достигнет s. Пусть Ai,k - количество циклических расположений, при которых < tok,pi> передается ровно k раз. Тогда суммарное число пересылок < tok,pi> равно.
|
|
|


