 |
Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.
|
|
|
|
Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для других систем. Допустим, что имеется некоторое целое число N8 в 8-ой системе. Оно может быть представлено в виде:
N8 = a1*8n-1 + a2*8n-2 + a3*8n-3 +... + an-2*82 + an-1*81 + an*80.Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.:
N2 = b1*2k-1 + b2*2k-2 +... + bk-2*22 + bk-1*21 + bk*20.Разделим эти выражения на 23 = 8:
a1*8n-2 + a2*8n-3 + a3*8n-4 +... + an-1*80 + an*8-1 ------- дробная часть b1*2k-4 + b2*2k-5 +... + bk-3*20 + bk-2*2-1 + bk-1*2-2 + bk*2-3 ------------------------- дробная частьТак как числа были равны, то получается одинаковые частные и одинаковые остатки:
an*8-1 = bk-2*2-1 + bk-1*2-2 + bk*2-3.Если снова разделим целые части на 23 = 8, то опять получим равные частные и равные остатки.
При этом видим, что каждой восьмеричной цифре соответствует её двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы её двоичным эквивалентом и обратно.
Пример:
62,7538 = 110010,1111010112Аналогично для 4-ой системы:
321,22334 = 111001,101011112Аналогично для 16-ой системы:
1D876,72 = 00011101100001110110,011100102Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись.

| bk-2 | bk-1 | bk | an |
Если умножить последние соотношения на 8, то:
an*8-1*8 = (bk-2*2-1 + bk-1*2-2 + bk*2-3)*23an = bk-2*22 + bk-1*21 + bk*20Практически перевод двоичного числа в восьмеричное, шестнадцатеричное и обратно очень прост. Покажем это на примере:




 3 5 0 6 тетрады 350616
3 5 0 6 тетрады 350616
|
|
|
 0 0 1 1 0 1 0 1 0 0 0 0 0 1 1 0
0 0 1 1 0 1 0 1 0 0 0 0 0 1 1 0
 3 2 4 0 6 триады 324068
3 2 4 0 6 триады 324068
Все позиционные системы одинаковы, в том смысле, что арифметические действия выполняются по одним и тем же правилам.
Пример 2.
 |  | ||||||||||||
 |  |  |  |  | |||||||||
 16-теричное 4 D 1 3 A 5 E
16-теричное 4 D 1 3 A 5 E








 2-ичное 0 1 0 0 1 1 0 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 1 0
2-ичное 0 1 0 0 1 1 0 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 1 0
8-ричное 4 6 4 2 3 5 1 3 2
Пример 3
(11010011)2 = Х10
(17)10 =Х2
Проблема представления отрицательных чисел
Основное неудобство построения устройств, реализующих арифметические операции, состоит в сложном характере алгоритма вычитания. Для его преодоления в ЭВМ всегда операция выполняется по иным правилам, чем это делается обычно. В его основе лежит операция сложения. Алгоритмы выполнения такого рода операций требуют специальных кодов представления отрицательных чисел.
Прямой код.
Это естественное и наиболее привычное представление числа в следующем виде:
знак: "+" соответствует 0
"-" соответствует 1
В цифровых разрядах пишется модуль положительного или отрицательного числа.
[X]пк - обозначим таким образом изображение числа "X" в прямом виде.

Рассмотрим диапазоны представляемых чисел:
X+min = 0,000....0 - изображение положительного нуля
X+max = 0,111....1 = 1 - 2-n
X-min = 1,111....1 = -(1-2-n)
X-max = 1,000....0 - изображение отрицательного нуля.
Таким образом, нуль имеет двоякое изображение.
Замечания.
1. Перед выполнением операции вычитания чисел с одинаковыми знаками и сложения с разными, необходимо сравнить по модулю два кода и, если нужно, сделать перестановку кодов местами, затем можно выполнять собственно операцию вычитания кодов.
2. При выполнении операции умножения отдельно и независимо находятся модули произведений кодов, а знак находится как результат операции сложения по модулю два:
3. [X]пк * [Y]пк = sign Z. |Z|4. |Z| = |X|*|Y|5. sign Z = sign X sign Y или Sz = Sx
sign Y или Sz = Sx  Sy
Sy Собственно умножение выполняется с применением микроопераций сложения и сдвига.
|
|
|
Аналогично умножению выполняется операция деления с использованием микроопераций вычитания и сдвига.
Вследствие ряда неудобств в ЭВМ операции вычитания, сложения чисел с разными знаками и деления в прямом коде практически не выполняются.
Дополнительный код.
Дополнительным называется код, в котором для положительного числа в знаковом разряде пишется "0", в цифровых - модуль числа, а для отрицательного в знаковом разряде пишется "1", в цифровых - дополнение числа до единицы.

Если некоторое X- = -0,  1
1  2…
2…  n нужно представить в дополнительном коде, то
n нужно представить в дополнительном коде, то

где: 1 - 0,  1
1  2…
2…  n = 0, Z1Z2…Zn
n = 0, Z1Z2…Zn
Диапазоны представленных чисел:
Х+ min = 0,0…0 - положительный нуль
Х+ max = 0,11…1 = 1-2-n - максимальное положительное число.
X- min = 1,11…1 = 2-2-n - минимальное отрицательное число
X- max = 1,0…0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
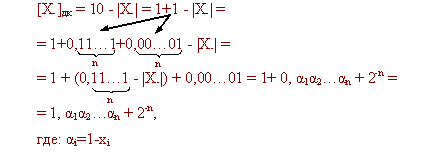
Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
1. X+ + Y+ = S+
2. X+ + Y- = S+
3. X+ + Y- = S-
4. X- + Y- = S-
Необходимо помнить, что нельзя, выполняя операции, выходить за диапазон представляемых в данной разрядной сетке чисел, записанных с фиксированной запятой.
Положим n = 3, 1 - знаковый разряд и 2 - цифровых.
1. X+ = 0,10 2. Y+ = 0,103. В дополнительном коде

То есть, нет никаких особенностей.
4. X+ = 0,105. Y- = -0,016. В дополнительном коде

Переполнение теряется и получается верный результат.
7. X+ = 0,018. Y- = -0,119. В дополнительном коде

12. В дополнительном коде

Возникающее переполнение теряется и общий результат отрицательный.
|
|
|
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровым. Возникающие переносы теряются и не влияют на результат операции.
Обратный код.
Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.

Определим диапазон чисел:
X+ min = 0,00…0 - положительный нуль.
X+ max = 0,111…1 = 1 - 2-n
X- min = 1,11…1 0 = 2 - 2-n+1
X- max = 1,00…00 = 1
В обратном коде есть два изображения нуля:
"Положительный" нуль:
[X]ок = 0,0…0и "отрицательный" нуль:
[X]ок = 1,11…11При этом
X - X = [X+]ок + [X-]ок = |X+| + 10 - (10)-n - |X-| = +10 - (10)-n = 0или 10 ~ (10)-n
То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.
Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.
1. X+ = 0,102. Y- = -0,01 3. X+ + Y- = S+4. В обратном коде:

Возникающее переполнение должно быть добавлено к младшему разряду частичной суммы.
5. X+ = 0,106. Y+ = +0,017. X+ + Y+ = S+8. В обратном коде:

Нет никаких особенностей по сравнению с прямым кодом.
9. X+ = 0,0110. Y- = -0,1011. X+ + Y- = S-12. В обратном коде:

То есть, не возникает циклического переноса.
13. X- = -0,01 14. Y- = -0,10 15. X- + Y- = S-16. В обратном коде:

Возникает переполнение знакового разряда, которое добавляется в младший разряд частичной суммы.
Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперция инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.
Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно под всеми цифровыми разрядами числа.
Дадим практический метод получения двоичного числа в дополнительном коде (без математического обоснования):
|
|
|
1. проинвертировать все биты исходного числа;
2. к полученному результату прибавить 1(или другими словами проинвертируем все цифры вплоть до последнего разряда).
Пример:
Пусть требуется получить двоичное значение десятичного числа: - 510. Формат числа 16-ти разрядное слово.
Итак:
510 = 0000 0000 0000 0101
инверсия 1111 1111 1111 1010
добавим +1, получим требуемое двоичное число, эквивалентное -510
1111 1111 1111 10112
Здесь необходимо особое внимание уделять старшему разряду, он называется «знаковым».
0 – для знака плюс и 1 – для знака минус. При определении величины числа знак разряда не используется, т.е. мы имеем 15-ти разрядное двоичное число. Сложение двоичного числа с его дополнительным кодом всегда дает нулевой результат.
Таким образом, можно сказать, что если исходное число положительное, то в знаковый разряд записываем «0», а информационную часть числа записываем без изменений.
Если число отрицательное, тогда в знаковый разряд записываем «1», а информационную част числа инвертируем до последней значащей цифры.
Иногда находит применение обратный код.Что касается положительного числа, то здесь правила записи не отличаются от правил записи чисел в прямом и обратном коде. Если число отрицательное, то в знаковый разряд записывается «1», а информационная часть числа полностью инвертируется.
Однако, двоичная запись числа не всегда удобна (длинная), поэтому в компьютерной технике часто применяют сокращенную нотацию двоичных чисел – восьмеричную и шестнадцатеричную системы счисления.
Вопросы и задания:
1. Преобразуйте (1001101001)2 в Х10, Х8 и Х16.
2. Примеры на действия с двоичными числами.
|
|
|


