 |
Векторная алгебра и аналитическая геометрия
|
|
|
|
Математика
Программа, методические указания и задания контрольной и самостоятельной работы для студентов заочной формы обучения направления:
«Торговое дело-100700.62», «Менеджмент-080200.62»
Сокращенная образовательная программа
Квалификация выпускника - бакалавр
Новосибирск 2011
Кафедра общегуманитарных дисциплин
Математика: Программа, методические указания и задания контрольной работы 1 для студентов заочной формы обучения направления «Торговое дело-100700.62», «Менеджмент-080200.62»
Составитель: Вахромеева Т.В., доцент, Новосибирск: НФ РГТЭУ - 2011, 33 стр.
Рецензент: Бертик И.А.,доцент кафедры общегуманитарных дисциплин НФ РГТЭУ
Методические указания рекомендованы к изданию кафедрой общегуманитарных дисциплин, протокол от «17» ноября 2011г.
Содержание
1. Правила выбора варианта контрольной работы................ 4
2. Объем дисциплины............................... 5
3. Содержание дисциплины................................... 6
4. Вопросы для подготовки к экзамену.......................... 11
5. Варианты контрольной работы............................ 24
6. Методические указания для решения задач................... 36
Правила выбора варианта контрольной работы, ее оформление и зачета
1. В процессе изучения высшей математики студент первого курса должен выполнить две контрольные работы, задачи второй из которых содержатся в разделе «Варианты контрольной работы». Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
|
|
|
2. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины (высшая математика), номер контрольной работы, номер варианта и домашний адрес студента. В конце работы следует поставить дату ее выполнения и расписаться.
5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.
7. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.
Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа p, e и т. д.
Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Так, например, вычислив неопределенный интеграл, нужно проверить, равна ли подынтегральная функция производной от полученной первообразной. Полезно также, если это возможно, решить задачу несколькими способами и сравнить полученные результаты.
8. Срок проверки контрольных работ – 10 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 10 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.
|
|
|
9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. В связи с этим рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается.
10. Прорецензированные контрольные работы вместе со всем.и исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять.
На экзамен студент должен явиться с рецензией на выполненную контрольную работу. Без предъявления преподавателю прорецензированных контрольных работ студент к экзамену не допускается.
ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
| Вид учебной работы | Всего часов / зачетных единиц | Семестр | |
| Аудиторные занятия (всего) | |||
| В том числе: | - | - | |
| Лекции | |||
| Практические занятия (ПЗ) | |||
| Семинары (С) | - | - | |
| Самостоятельная работа (всего) | |||
| В том числе: | - | - | |
| Подготовка к экзамену | |||
| Подготовка к зачету | |||
| Другие виды самостоятельной работы | - | - | |
| Выполнение контрольных работ | |||
| Работа с учебным материалом | |||
| экзамен | |||
| Общая трудоемкость часы зачетные единицы | |||
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Содержание разделов дисциплины
Линейная алгебра
Системы линейных уравнений (СЛУ). Понятие матрицы, ранг матрицы. Метод Гаусса. Теорема Кронекера – Капелли.
Понятие определителя n-го порядка. Способы вычисления и свойства определителей. Формулы Крамера для решения систем линейных уравнений. Операции с матрицами и их свойства. Обратная матрица и способы ее нахождения. Матричная запись системы линейных уравнений. Решение системы линейных уравнений с помощью обратной матрицы.
|
|
|
Формируемые компетенции: ПК-1, ПК-3.
Векторная алгебра и аналитическая геометрия
Понятие n-мерного вектора и n-мерного арифметического пространства 
. Свойства операций с векторами. Геометрический смысл пространств 
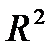и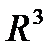 
. Скалярное произведение векторов в и его свойства. Длина вектора, угол между векторами.
Координатный метод. Различные виды уравнения прямой в пространстве и на плоскости. Угол между прямыми, условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой. Понятие о кривых второго порядка: эллипсе, гиперболе, параболе. Уравнения прямой и уравнения плоскости в пространстве 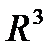. Расстояние от точки до плоскости.
Формируемые компетенции: ПК-1, ПК-3.
3. Введение в математический анализ. Понятие функции. Предел и непрерывность функций
Цели, задачи, предмет и метод дисциплины. Межпредметные связи дисциплины “Математика”, ее роль и место в естественнонаучном цикле дисциплин.
Понятие функции. Способы задания функций. Элементарные функции. Простейшие неэлементарные функции. Числовая последовательность и ее предел. Предел функции. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции. Односторонние пределы. Два замечательных предела. Непрерывность функции. Свойства непрерывных функций.
Формируемые компетенции: ПК-1, ПК-3.
|
|
|
