 |
Методические рекомендации к выполнению контрольной работы
|
|
|
|
Линейная алгебра и элементы аналитической геометрии
Для решения задачи 1 и задачи 2 необходимо изучить следующую литературу: [1,4,5,6]
Теперь рассмотрим применение изученных формул на примерах.
ЗАДАЧА 1.
Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

Решение.
а) Метод Крамера состоит в решении системы линейных уравнений по формулам Крамера  ,
,
где  (Подробности смотрите в пункте з) задачи 1.
(Подробности смотрите в пункте з) задачи 1.
Так как 


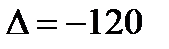 ; то
; то 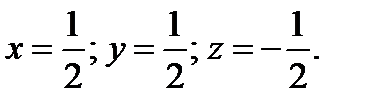
б) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последнего уравнения легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.


Поменяем местами первую и вторую строки матрицы, чтобы в ее левом верхнем углу была единица. Получим матрицу,


Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид,

 =
= 

Умножим каждый элемент первой строки матрицы на – 3 и прибавим полученные числа к соответствующим элементам третьей строки. Получим:

 =
= 
 .
.
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.

 .
.
Умножим каждый элемент второй строки матрицы на – 8 и прибавим полученные числа к соответствующим элементам третьей строки:



 .
.
Данная матрица соответствует системе уравнений  , решение которой совпадает с решением исходной системы. Начиная с последнего уравнения несложно найти все неизвестные.
, решение которой совпадает с решением исходной системы. Начиная с последнего уравнения несложно найти все неизвестные.
|
|
|
Действительно, так как  и
и 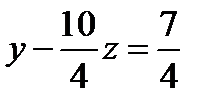 , то
, то 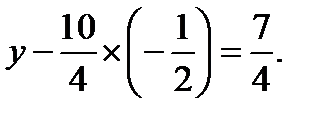
Отсюда,  Из
Из  имеем
имеем 
Ответ:  .
.
в) решение системы в этом случае равно 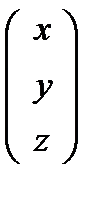 =
= 
 , где
, где  =
=  – обратная матрица для матрицы
– обратная матрица для матрицы  =
=  ,
,  – столбец свободных членов,
– столбец свободных членов,  – определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
– определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
Составим матрицу состоящую из коэффициентов при неизвестных данной системы:
А =  .
.
Вычислим ее определитель  = – 4
= – 4  – 4
– 4  – 6
– 6  =
= 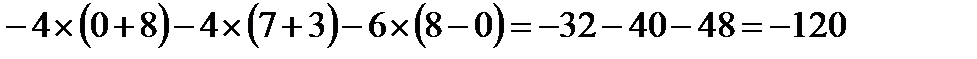 .
.
Вычислим алгебраические дополнения для всех элементов матрицы А:








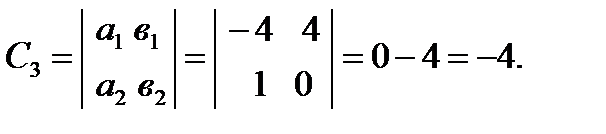
Тогда 
 =
=  =
=  и
и  =
= 

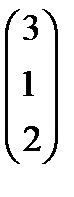 =
=
=  =
=  =
=  =
= 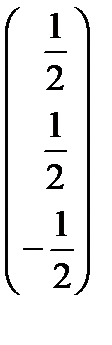 .
.
Отметим, что ответы, полученные при решении разными методами совпадают между собой.
Ответ: 
ЗАДАЧА 2.
В декартовой прямоугольной системе координат даны вершины пирамиды А1 В1 С1 D1. Найдите:
а) длину ребра А1 В1;
б) косинус угла между векторами  ;
;
в) уравнение ребра А1 В1;
г) уравнение грани А1 В1 С1;
д) уравнение высоты, опущенной из вершины D1 на грань А1 В1 С1;
е) координаты векторов  ,
,  ,
,  , и докажите, что они образуют линейно независимую систему;
, и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где
, где 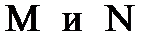 — середины ребер А1 D1 и В1 С1, соответственно;
— середины ребер А1 D1 и В1 С1, соответственно;
з) разложение вектора  по базису
по базису  если А1(- 2,2,2), В1(1, - 3,0), С1(6,2,4), D1(5,7, - 1).
если А1(- 2,2,2), В1(1, - 3,0), С1(6,2,4), D1(5,7, - 1).
Решение.
а) найдем координаты вектора  по формуле:
по формуле:
 =
=  XВ
XВ  - XА
- XА  ; YВ
; YВ  - YА
- YА  ; ZВ
; ZВ  - ZА
- ZА 
 , где (ХА
, где (ХА  , YА
, YА  , ZА
, ZА  ) – координаты точки А1, (ХВ
) – координаты точки А1, (ХВ  , YВ
, YВ  , ZВ
, ZВ  ) – координаты точки В1.
) – координаты точки В1.
Итак,  =
=  Тогда
Тогда  =
=  .
.
Итак, длина отрезка  (или длина вектора
(или длина вектора  ) равна
) равна  . Это и есть искомая длина ребра.
. Это и есть искомая длина ребра.
б) координаты вектора  =
=  уже известны, осталось определить координаты вектора
уже известны, осталось определить координаты вектора  :
:  =
=  .
.
Угол между векторами  и
и 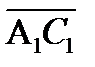 вычислим по формуле:
вычислим по формуле:
cos  =
=  ,
,
где скалярное произведение векторов  и
и 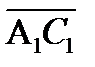 равно (
равно ( ,
,  )= 3 ´ 8 + (- 5) ´ 0 + (- 2) ´2 =24 + 0 - 4=20,
)= 3 ´ 8 + (- 5) ´ 0 + (- 2) ´2 =24 + 0 - 4=20,  =
=  ,
,  =
=  Итак, cos
Итак, cos  =
=  =
=  .
.
в) координаты точки А1(- 2,2,2) обозначим соответственно Х0 = - 2, У0 = 2, Z0=2, а координаты точки В1 (1, - 3,0) через Х1=1, У1 = - 3, Z1=0 и воспользуемся уравнением прямой в пространстве, проходящей через две точки:  .
.
Следовательно, уравнение ребра А1В1 имеет вид  или
или 
|
|
|
г) обозначим координаты векторов  и
и 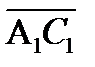 через Х1=3, У1= - 5,
через Х1=3, У1= - 5, 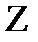 1= - 2 и Х2=8, У2= 0,
1= - 2 и Х2=8, У2= 0, 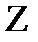 2=2, соответственно. Векторное произведение данных векторов определяется формулой
2=2, соответственно. Векторное произведение данных векторов определяется формулой

Так как данный вектор перпендикулярен грани А1 В1 С1, то можно воспользоваться уравнением плоскости, проходящей через точку (Х0, У0, 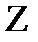 0) перпендикулярно вектору
0) перпендикулярно вектору  , которое имеет вид:
, которое имеет вид:
А  .
.
Подставим координаты точки А1 (Х0= - 2, У0=2, 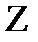 0=2) и координаты перпендикулярного вектора А= - 10, В= - 22, С=40 в это уравнение:
0=2) и координаты перпендикулярного вектора А= - 10, В= - 22, С=40 в это уравнение:
– 10 (Х + 2) - 22 (У - 2) + 40 (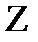 - 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (- 20 + 44 - 80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: - 10х - 22у + 40 z - 56=0 или - 5х - 11у + 20 z - 28=0.
- 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (- 20 + 44 - 80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: - 10х - 22у + 40 z - 56=0 или - 5х - 11у + 20 z - 28=0.
д) вектор  является направляющим вектором высоты, опущенной из вершины D 1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку
является направляющим вектором высоты, опущенной из вершины D 1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку  с заданным направляющим вектором:
с заданным направляющим вектором:  , где
, где  – координаты точки D1. Отсюда искомое уравнение:
– координаты точки D1. Отсюда искомое уравнение:  или
или 
е) координаты вектора  =
=  =
=  .
.
Обозначим 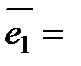
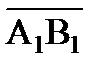 =
=  ,
, 
 =
= 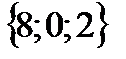 ,
,  .
.
Чтобы доказать, что векторы  образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
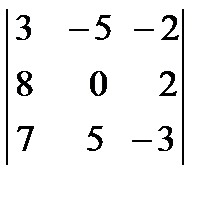 отличен от 0. Определитель третьего порядка равен
отличен от 0. Определитель третьего порядка равен
 =
= 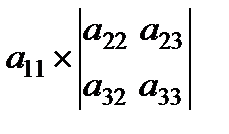 -
-  +
+  =
=
= 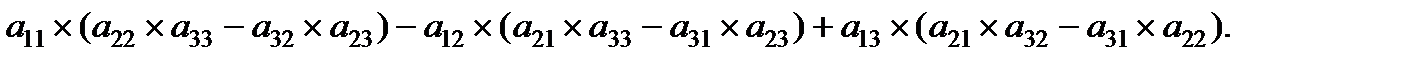
Вычислим определитель
 =3
=3  – (– 5)
– (– 5)  +(– 2)
+(– 2)  = 3
= 3  (0
(0  (– 3) – 5
(– 3) – 5  2)+5
2)+5  (8
(8  (– 3) – 7
(– 3) – 7  2) –
2) –
- 2  (8
(8  5 – 7
5 – 7  0) =3
0) =3  (– 10)+5
(– 10)+5  (– 24 – 14) – 2
(– 24 – 14) – 2  40= – 30 – 190 – 80 = – 300.
40= – 30 – 190 – 80 = – 300.
Так как данный определитель отличен от 0, то вектора  образуют линейно независимую систему.
образуют линейно независимую систему.
ж) сначала найдем координаты точек М и N, соответственно. Координаты точки
М = 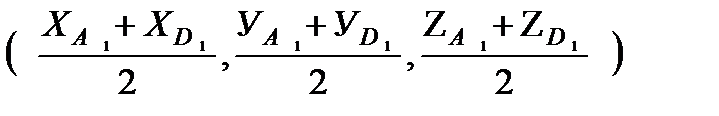 =
=  =
=  N =
N =  =
=  =
=  .
.
Получаем вектор  =
=  .
.
з) обозначим через  координаты вектора
координаты вектора  в базе
в базе  .
.
Тогда  =
=  =
=  .
.
Так как:  =
= 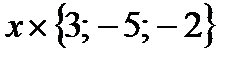 +
+  +
+ 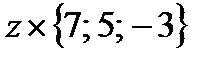 ;
; 
= 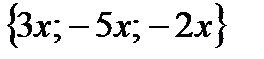 +
+  +
+  =
=  ,
,
то приравнивая соответствующие координаты, получим систему трех линейных уравнений с тремя неизвестными:
(1) 
Решим данную систему уравнений с помощью формул Крамера (см.  глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
(2) 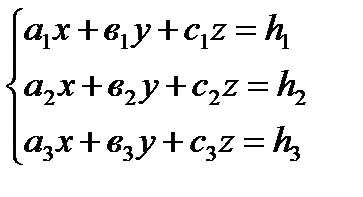
Тогда  =
= 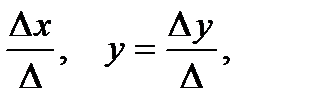 z
z 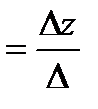 , где:
, где:

Для системы (1) определитель:
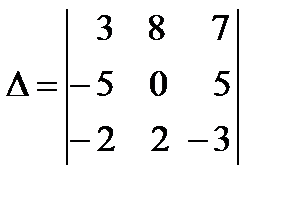 =3
=3  – 8
– 8 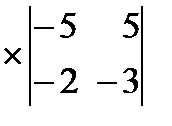 +7
+7  =
=
= 3 (– 10) – 8  (15 + 10) + 7 (– 10) = – 30 – 200 – 70 = – 300;
(15 + 10) + 7 (– 10) = – 30 – 200 – 70 = – 300;
 = 2
= 2 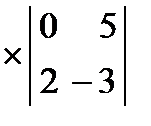 – 8
– 8  +7
+7 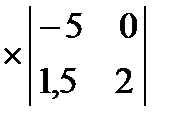 =
=

 =3
=3  – 2
– 2 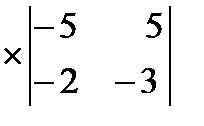 +7
+7  =
=
=3 
 =3
=3  – 8
– 8  +2
+2  =
=
= 
По формулам Крамера 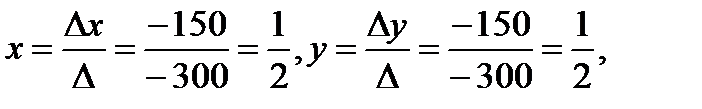
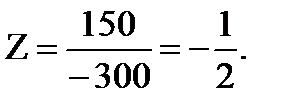
Итак, разложение вектора  по базису (
по базису ( ) имеет вид
) имеет вид
 =
= 
Задача 3. Для решения задачи 3 необходимо изучить  .
.
|
|
|
Задача 4. Найти производную функции z = x2 – xy + y2 в точке М0(1; 1):
а) в направлении вектора  ;
;
б) определить градиент z в точке М0(1; 1), его величину и направление.
Решение:
а) Функцией z = x2 – xy + y2 определено плоское скалярное поле в точке (х; у). Производная функции z = f(x; y) по данному направлению 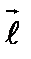 определяется формулой:
определяется формулой:
 , где cos a, cos b – направляющие косинусы вектора
, где cos a, cos b – направляющие косинусы вектора 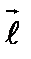 .
.
В задаче направление определено вектором  , его направляющие косинусы
, его направляющие косинусы
 .
.
Определим частные производные функции в точке М0(1; 1):
 .
.
Тогда производная по направлению равна 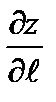 = 1×0,6+1×0,8 = 1,4 > 0. Производная по направлению определяет скорость изменения функции z(x, y) в этом направлении. Так как
= 1×0,6+1×0,8 = 1,4 > 0. Производная по направлению определяет скорость изменения функции z(x, y) в этом направлении. Так как 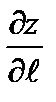 > 0, то в этом направлении функция z возрастает.
> 0, то в этом направлении функция z возрастает.
б) grad z есть вектор, указывающий направление набольшего возрастания поля в данной точке и имеющий модуль, равный скорости этого возрастания. Этот вектор определяется по формуле:
grad z = 
Следовательно, grad z =  .
.
|
|
|


