 |
Дифференциальное исчисление функций одной переменной
|
|
|
|
Определение производной. Дифференцируемость и непрерывность функций. Геометрический, физический и экономический смысл производной. Правила дифференцирования (включая производные сложной и обратной функции). Теоремы Ферма, Ролля, Лагранжа, Коши. Правило Лопиталя. Дифференциал функции, его связь с производной. Геометрический смысл дифференциала и его использование в приближенных вычислениях. Производные и дифференциалы высших порядков.
Исследование функций с помощью дифференциального исчисления. Условия возрастания и убывания функций. Экстремум функции. Необходимые и достаточные условия существования экстремума. Выпуклость графика функции. Точки перегиба и их нахождение. Асимптоты. Общая схема исследования функции.
Формулы Тейлора и Маклорена. Примеры разложения элементарных функций по формуле Маклорена.
Формируемые компетенции: ПК-1, ПК-3.
Дифференциальное исчисление функций нескольких переменных
Понятие функции нескольких переменных. Предел и непрерывность функций нескольких переменных. Частные производные 1-го и 2-го порядка. Дифференциал функции. Производная по направлению. Градиент и его свойства.
Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточные условия для случая двух независимых переменных. Нахождение наибольшего и наименьшего значения функции нескольких переменных. Условный экстремум. Метод множителей Лагранжа.
Формируемые компетенции: ПК-1, ПК-3.
Интегральное исчисление функций одной переменной
Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов. Основные методы интегрирования: замена переменной, интегрирование по частям..
|
|
|
Определенный интеграл как предел интегральных сумм. Свойства определенного интеграла. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Геометрические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения. Несобственные интегралы.
Формируемые компетенции: ПК-1, ПК-3.
Числовые и функциональные ряды
Числовые ряды. Сумма ряда. Необходимое условие сходимости ряда. Свойства рядов. Теорема сравнения. Признаки сходимости Даламбера, Коши. Знакочередующиеся ряды. Абсолютная и условная сходимость. Признак Лейбница.
Функциональные ряды. Степенные ряды. Радиус, интервал и область сходимости. Разложение элементарных функций в ряд Маклорена или Тейлора. Использование рядов для приближенных вычислений.
Формируемые компетенции: ПК-1, ПК-3.
Обыкновенные дифференциальные уравнения
Понятие о дифференциальном уравнении. Семейство решений. Теорема существования и единственности решения (без доказательства). Задача Коши. Геометрическое истолкование решения. Общее и частное решение дифференциального уравнения.
Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Линейное дифференциальное уравнение первого порядка. Метод вариации постоянной.
Линейные дифференциальные уравнения второго порядка. Структура общего решения. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Подбор частного решения при специальном виде правой части.
Формируемые компетенции: ПК-1, ПК-3.
Разделы дисциплины и виды занятий.
| № п/п | Наименование раздела дисциплины | Лек. | Практ. зан. | Сем. | СРС | Всего |
| 1. | Введение. Понятие функции. Предел и непрерывность функций | - | ||||
| 2. | Дифференциальное исчисление функций одной переменной | - | ||||
| 3. | Дифференциальное исчисление функций нескольких переменных | - | ||||
| 4. | Интегральное исчисление функций одной переменной | - | ||||
| 5. | Числовые и функциональные ряды | - | ||||
| 6. | Обыкновенные дифференциальные уравнения | - | ||||
| 10. | Линейная алгебра | - | ||||
| 11. | Векторная алгебра и аналитическая геометрия | - | ||||
| 12. | Основные понятия и основные теоремы теории вероятностей. Схема Бернулли | - | ||||
| 13. | Случайные величины, их функциональные и числовые характеристики | - | ||||
| 14. | Математическая статистика | - | ||||
| Всего | - |
|
|
|
Вопросы для подготовки к экзамену.
Математический анализ
1. Понятие функции. Способы задания функций. Примеры. Элементарные функции.
2. Числовая последовательность. Предел числовой последовательности. Примеры.
3. Предел функции (два определения). Основные теоремы о пределах. Второй замечательный предел.
4. Бесконечно малые и бесконечно большие функции. Первый замечательный предел, его геометрический смысл.
5. Предел функции. Непрерывность функции в точке. Точки разрыва функции и их классификация. Примеры.
6. Функции, непрерывные на отрезке (определение). Свойства функций, непрерывных на отрезке.
7. Производная функции её геометрический и механический смысл. Дифференцируемость и непрерывность
функции.
8. Производные элементарных функций.
9. Основные правила дифференцирования.
10. Дифференциал функции и его использование в приближенных вычислениях. Производные и дифференциалы
высших порядков.
11. Теорема Ферма (с доказательством).
12. Теорема Ролля (с доказательством).
13. Теорема Лагранжа (с доказательством).
14. Теорема Коши. Правило Лопиталя.
15. Возрастание и убывание функции. Исследование возрастания и убывания функции с помощью производной.
16. Экстремум функции. Необходимое условие экстремума. Достаточные условия экстремума.
17. Формулы Тейлора и Маклорена.
18. Выпуклость графика функции. Исследование выпуклости с помощью второй производной. Точки перегиба.
|
|
|
19. Асимптоты. Общая схема исследования функций.
20. Эластичность функции, анализ спроса и предложения.
21. Простейшие оптимизационные задачи в области коммерции.
22. Решение задачи о хранении вина.
23. Понятие функции нескольких переменных, предел и непрерывность, частные производные и дифференциал.
24. Производная функции двух переменных по направлению. Градиент и его свойства.
25. Необходимое и достаточное условия локального экстремума функции двух переменных.
26. Условный экстремум. Метод множителей Лагранжа.
27. Первообразная. Понятие неопределенного интеграла.
28. Свойства неопределенного интеграла. Табличные интегралы.
29. Замена переменной в неопределенном интеграле. Формула интегрирования по частям.
30. Определенный интеграл, его геометрический смысл и свойства. Формула Ньютона – Лейбница.
31. Замена переменной в определенном интеграле и интегрирование по частям.
32. Геометрические приложения определенного интеграла.
33. Приближенные методы вычисления определенного интеграла.
34. Несобственные интегралы. Определение, примеры.
35. Дифференциальные уравнения 1-го порядка, интегральные кривые. Общее и частное решения. Задача и теорема Коши.
36. Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
37. Линейные дифференциальные уравнения 1-го порядка. Теоремы об общем решении.
38. Метод вариации постоянных.
39. Линейные дифференциальные уравнения 2-го порядка. Теоремы об общем решении.
40. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
41. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
42. Числовые ряды. Необходимое условие сходимости ряда. Свойства сходящихся рядов.
43. Теорема сравнения рядов. Примеры применения теоремы.
44. Признак Даламбера сходимости ряда, интегральный признак Коши.
45. Знакопеременные ряды. Абсолютная и условная сходимость. Признак Лейбница.
46. Функциональные ряды. Область сходимости. Степенные ряды. Радиус и интервал сходимости. Примеры.
|
|
|
47. Ряды Тейлора и Маклорена. Разложение элементарных функций в ряд Маклорена.
Далее приведены варианты контрольной работы. Отметим, что номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки.
Вариант 0.
Задача 1. Решите систему линейных уравнений:
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы:
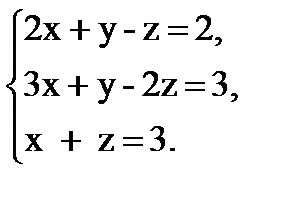
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами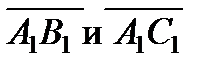 
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 
, 
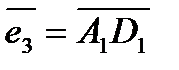и докажите, что они образуют линейно независимую систему;
ж) координаты вектора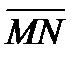 
, где M и N – середины ребер A1D1 и B1C1, соответственно;
з) разложение вектора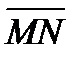 
по базису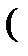 
,
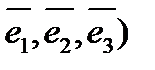если A1(1, - 1, 0), B1(2, 3, 1), C1(- 1, 1, 1), D1(4, - 3, 5).
Задача 3. Исследовать и построить график функции 
Задача 4. Дана функция 
, точка А(1;1) и вектор 
=(2;1). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = –x 2–5 x –6; y = x +2.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
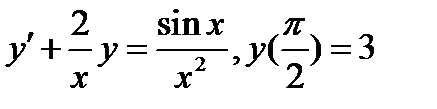
Вариант 1.
Задача 1. Решите систему линейных уравнений:
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
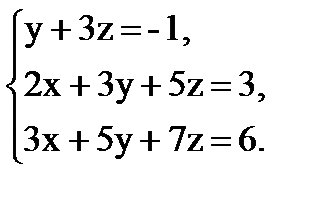
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A 1 B 1;
б) косинус угла между векторами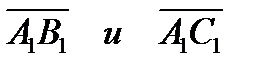 
;
в) уравнение ребра A1B1;
г) уравнение грани A 1 B 1 C 1;
д) уравнение высоты, опущенной из вершины D 1 на грань A 1 B 1 C 1;
е) координаты векторов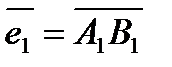 
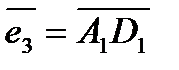, и докажите, что они образуют линейно независимую систему;
ж) координаты вектора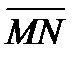 
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 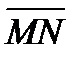по базису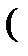 
,
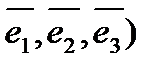если A1(2, 0, - 3), B1(1, 1, 1), C1(4, 6, 6), D1(- 1, 2, 3).
Задача 3. Исследовать и построить график функции y=x 3 - 9 x 2 + 24 x- 16
Задача 4. Дана функция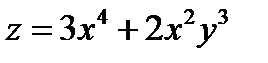 
, точка А(-1;2) и вектор =(4;-3). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–5 x +5; y = x –3.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
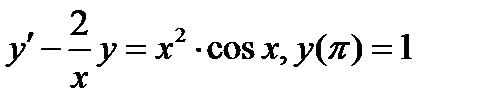
Вариант 2.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
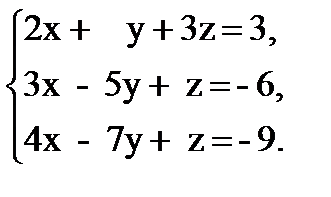
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами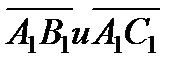 
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
|
|
|
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 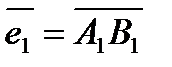, 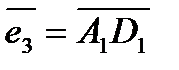и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 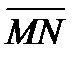, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 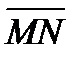по базису ,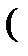
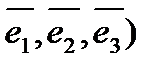если A1(- 3, 1, 1), B1(0, - 4, - 1), C1(5, 1, 3), D1(4, 6, - 2).
Задача 3. Исследовать и построить график функции 
Задача 4. Дана функция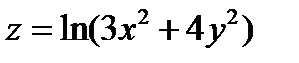 
, точка А(1;3) и вектор =(2;-1). Найти grad z в точке А, производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = –x 2–11 x –30; y = x +5.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
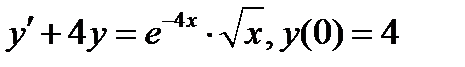
Вариант 3.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами 
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 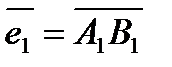, 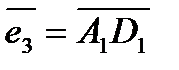и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 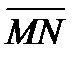, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 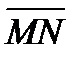по базису ,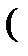
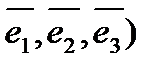если A1(1, 1, 4), B1(2, 1, 2), C1(1, - 1, 2), D1(6, - 3, 8).
Задача 3. Исследовать и построить график функции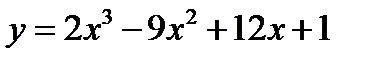 
Задача 4. Дана функция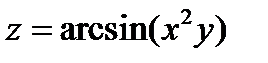 
, точка А(1;2) и вектор =(5;-12). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–5 x +8; y = x.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
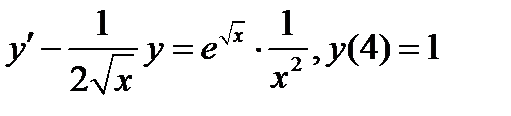
Вариант 4.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
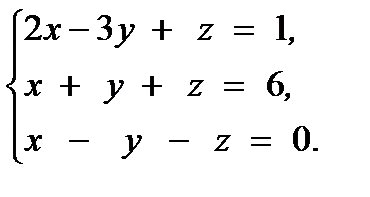
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами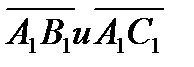 
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 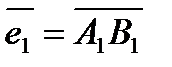, 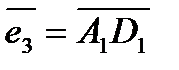и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 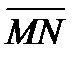, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 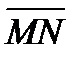по базису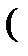 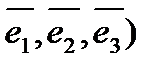, если
A1(2, 1, - 4), B1(- 3, - 5, 6), C1(0, - 3, - 1), D1(- 5, 2, - 8).
Задача 3. Исследовать и построить график функции y=x 3 + 6 x 2 + 9 x+ 4.
Задача 4. Дана функция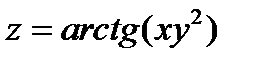 
, точка А(2;3) и вектор =(4;-3). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–5 x +7; y = x –1.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
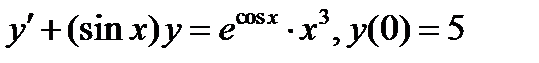
Вариант 5.
Задача 1. Решите систему линейных уравнений:
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
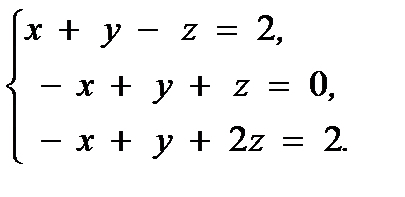
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами ;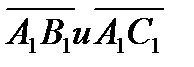
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов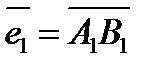 
, 
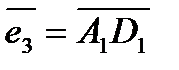и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 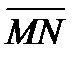, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора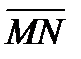 
по базису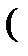 
,
если A1(3, 0, 1), B1(1, 3, 0), C1(4, - 1, 2), D1(- 4, 3, 5).
Задача 3. Исследовать и построить график функции y=x 3 +x 2 -5x+3
Задача 4. Дана функция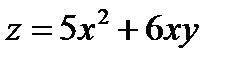 
, точка А(2;1) и вектор =(1;2). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–7 x +12; y = x –3.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
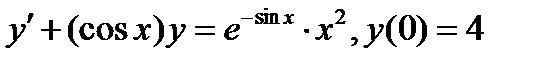
Вариант 6.
Задача 1. Решите систему линейных уравнений:
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
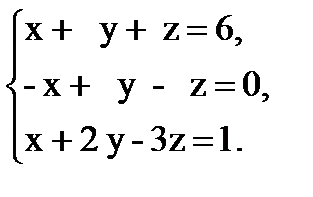
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами ;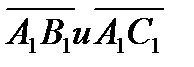
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 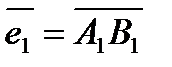, 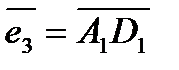и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 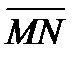, где M и N – середины ребер A1D1 и B1C1, соответственно;
з) разложение вектора 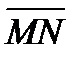по базису ,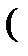
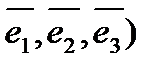если A1(3, 0, - 1), B1(- 1, - 2, - 4), C1(- 1, 2, 4), D1(7, - 3, 1).
Задача 3. Исследовать и построить график функции y=x 3 - 10 x 2 + 28 x- 24
Задача 4. Дана функция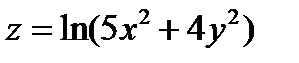 
, точка А(1;1) и вектор =(2;-1). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = –x 2–5 x –1; y = x +7.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
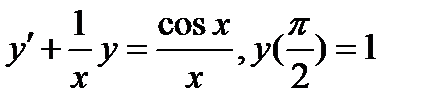
Вариант 7.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами ;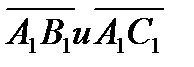
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 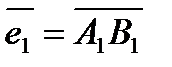, 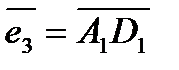и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 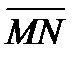, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 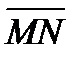по базису ,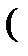
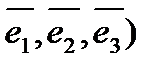если A1(2, - 2, 1), B1(1, 2, - 1), C1(1, 0, 2), D1(2, 1, 0).
Задача 3. Исследовать и построить график функции y=x 3 + 9 x 2 + 24 x+ 20
Задача 4. Дана функция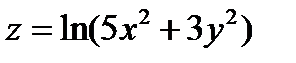 
, точка А(1;1) и вектор =(3;2). Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–3 x +4; y = x +1.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
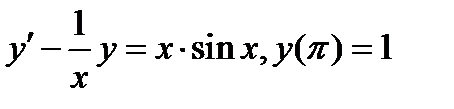
Вариант 8.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
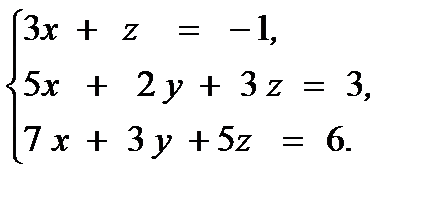
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами ;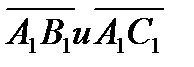
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 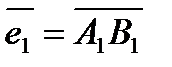, 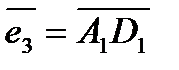и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 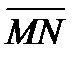, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 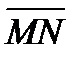по базису ,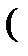
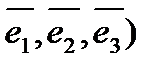если A1(1, - 1, 1), B1(2, 1, - 1), C1(- 2, 0, 3), D1(2, - 2, - 4).
Задача 3. Исследовать и построить график функции y=x 3 - 11 x 2 + 39 x- 45
Задача 4. Дана функция 
, точка А(2;1) и вектор =(3;-4).
Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = –x 2–7 x –12; y = x +3.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
Вариант 9.
Задача 1. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
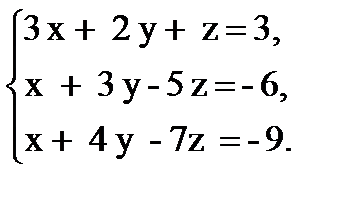
Задача 2. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами ;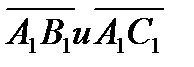
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 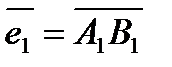, 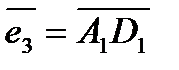и докажите, что они образуют линейно независимую систему;
ж) координаты вектора 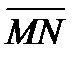, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора 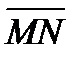по базису ,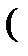
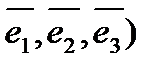если A1(0, 1, - 1), B1(- 3, 0, 1), C1(1, 2, 0), D1(1, - 1, 2).
Задача 3. Исследовать и построить график функции y=x 3 - 12 x 2 + 45 x- 54
Задача 4. Дана функция 
, точка А(1;1) и вектор =(2;-1) Найти grad z в точке А и производную в точке А в направлении вектора .
Задача 5. Найти площадь фигуры, заключенную между линиями.
y = x 2–5 x +6; y = x –2.
Задача 6. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям
|
|
|
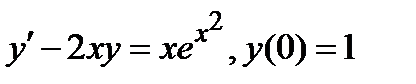
