 |
Основные виды реакции элементов РЭС на механические воздействия
|
|
|
|
| Элементы РЭС | Возможный механический отклик | Возможный электрический отклик | Защитные мероприятия |
| Резисторы и конденсаторы: а) дискретные б) пленочные в) переменные ПП, ИМС Реле, разъемы, переключатели, герконы Провода и кабели | Разрушение мест пайки, обрывы выводов Трещины в пленке Поворот оси ротора и смещение пластин КПЕ Поворот оси резистора Обрывы выводов, разрушение мест пайки. Деформация и растрескивание подложек ИМС Взаимное перемещение контактных элементов Перемещения в пространстве, деформация и обрывы, особенно в местах пайки | Разрыв электрической цепи, тензоэффект Изменение значения емкости Изменение значения сопротивления Пьезоэффект, тензоэффект Переменное значение переходного сопротивления Виброшумы за счет электромагнитной индукции и кабельного эффекта | Исключение резонансных колебаний. Размещение элементов на участках подложек с минимальной деформацией. Стопорение оси контргайками, гровер-шайбами, нитроклеем или лаком Дополнительное крепление компаундом. Размещение элементов на участках плат с минимальной деформацией Определенная ориентация контактных групп относительно вектора воздействующих вибраций Вязка в жгуты, дополнительные точки крепления, использование антивибрационного кабеля, например, типа АВК-6 |
6.2.5. Защита конструкций РЭС от вибраций
ПРОЧНОСТЬ к воздействию механических факторов – это способность изделий выполнять свои функции и сохранять свои параметры в пределах норм, установленных в стандартах, после воздействия механических факторов.
|
|
|
УСТОЙЧИВОСТЬ к воздействию механических факторов – это способность изделий выполнять свои функции и сохранять свои параметры в пределах норм, установленных в стандартах, во время воздействия механических факторов.
К изделиям, предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования по прочности и устойчивости. К изделиям, не предназначенным для функционирования в условиях воздействия механических нагрузок, предъявляют требования только по прочности.
Как следует из приведенных выше определений для прочности и устойчивости, обеспечение устойчивости является более сложной технической задачей, чем обеспечение прочности.
Способы защиты конструкций РЭС от вибраций удобно классифицировать и наглядно представить, если использовать зависимость коэффициента динамичности 
от частоты 
. С использованием этой зависимости способы виброзащиты можно подразделить на три разновидности (рис. 6.24).
Рис.6.24. Способы виброзащиты:
а – увеличение жесткости конструктивных элементов (увеличение 
);
б – использование конструктивных элементов с увеличенной степенью демпфирования; в – использование виброизоляторов
На рис. 6.24 представлено соотношение собственной резонансной частоты защищаемого конструктивного элемента относительно диапазона частот воздействующих вибраций от fн до fв. Как следует из приведенного рисунка, вывод резонансной частоты элемента за пределы диапазона частот воздействующих вибраций в более высокочастотную область позволяет в диапазоне частот воздействующих вибраций обеспечить значение коэффициента динамичности 
. Это означает, что резонансного возбуждения колебаний защищаемого элемента происходить не будет. Подобное смещение значения в более высокочастотную область можно обеспечить увеличением жесткости конструктивных элементов.
|
|
|
Примеры конструктивного исполнения элементов аппаратуры, обладающих повышенной жесткостью, представлены на рис. 6.25.
Рис. 6.25. Конструктивные решения, позволяющие увеличить жесткость:
а – применение дополнительных точек или площадок крепления с помощью клея; б – применение дополнительных точек крепления;
в – применение отбортовок и профилирования (для пластин из металла);
г – применение ребер жесткости
На рис. 6.24, б показано изменение хода зависимости от при использовании конструктивных элементов, обладающих повышенной степенью демпфирования (пунктирная кривая). Большую степень демпфирования колебаний можно обеспечить, например, используя платы с вибропоглощающим покрытием, слоистые конструкции либо используя заливку поверхности платы с элементами демпфирующими материалами.
На рис. 6.26 представлены подобные конструктивные решения.
|
|
Рис. 6.26. Демпфированные конструкции:
а – с вибропоглощающим покрытием 2; б – с вибропоглощающим слоем 2;
в – с вибропоглощающим заливочным материалом 2
Применение демпфирующих покрытий и слоистых конструкций позволяет снизить значения коэффициентов динамичности таких конструктивных элементов, как печатные платы с нескольких десятков до нескольких единиц, причем в области их резонансных колебаний.
К недостаткам этого способа виброзащиты следует отнести ухудшение ремонтоспособности РЭС, зависимость характеристик покрытий и заливок от температуры, возникновение больших внутренних напряжений в компаунде при его полимеризации, изменение свойств покрытий и заливок с течением времени. Кроме того, величина рассеяния энергии механических колебаний полимерными материалами зависит от частоты, амплитуды и формы колебаний, состава компонентов, вида напряженного состояния. Эти обстоятельства усложняют аналитическую оценку эффективности виброзащиты, и в данном случае рациональнее использовать экспериментальные методы определения коэффициента механических потерь η через логарифмический декремент затухания колебаний
или через механическую добротность
Некоторые экспериментальные методы определения логарифмического декремента затухания колебаний конструкции изложены в п. 6.2.3 данного пособия.
|
|
|
Наиболее эффективным способом виброзащиты является виброизоляция, так как только в этом случае удается получить значения коэффициента динамичности < 1 в диапазоне частот воздействующих вибраций (см. рис. 6.24). Подобный способ виброзащиты может быть использован как для блоков, так и для отдельных, чувствительных к вибрациям элементов аппаратуры. Виброизоляция обеспечивается тем, что между защищаемым аппаратом или его элементом и вибрирующей поверхностью устанавливаются специальные элементы - виброизоляторы. Некоторые схемы монтажа блоков на виброизоляторах представлены на рис. 6.27.
Рис. 6.27. Схемы монтажа блоков аппаратуры на виброизоляторах
Установка блоков на виброизоляторах обеспечивает значение их собственных частот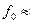 
10...25 Гц. В этом случае, начиная с частот 30–40 Гц, обеспечивается эффективная защита блока от вибраций ( < 1) и чем выше частота воздействующей вибрации, тем эффективнее виброзащита.
Используемые в настоящее время виброизоляторы можно подразделить на 4 основные разновидности:
1) резинометаллические;
2) пружинные с воздушным демпфированием;
3) пружинные с фрикционным демпфированием;
4) цельнометаллические.
В качестве примера конструктивного исполнения виброизолятора на рис. 6.28 показан вид пружинного виброизолятора с воздушным демпфированием. Демпфирование колебаний в данной конструкции обеспечивается движением воздуха через небольшое отверстие в резиновом баллончике 2.
Рис. 6.28. Виброизолятор пружинный с воздушным демпфированием:
1 – пружина; 2 – резиновый баллончик с отверстием;
3 – элемент крепления.
Оценку эффективности виброизоляции в первом приближении можно осуществить следующим образом:
1.Определяют значение собственной резонансной частоты блока на виброизоляторах:
где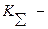 
суммарная жесткость системы виброизоляции;
масса блока.
2. Определяют значения амплитуды вынужденных колебаний блока либо значения коэффициента динамичности блока на виброизоляторах в диапазоне частот воздействующих вибраций:
|
|
|
или 
где 
амплитуда колебаний основания в месте монтажа блока;
текущее значение частоты вибрации;
собственная резонансная частота блока на виброизоляторах.
3. По известным значениям амплитуды колебаний блока и частоты вибрации определяют значение возникающего ускорения и сравнивают его с допустимым:
.
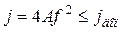Оценку эффективности виброизоляции по такой методике можно осуществить с помощью ЭВМ. Блок-схема алгоритма подобного расчета приведена на рис. 6.29. Она позволяет из совокупности виброизоляторов, данные о которых введены в память ЭВМ, выбрать те, которые обеспечивают необходимую степень виброизоляции по величине амплитуды колебаний блока. В данной блок-схеме может быть использован и другой критерий оценки эффективности виброизоляции – виброускорение.
Риc. 6.29. Блок-схема алгоритма выбора виброизоляторов с помощью ЭВМ
6.2.6. Защита РЭС от ударов, линейных нагрузок и акустических шумов
Реакция элементов и блоков РЭС на ударные нагрузки определяется не только величиной амплитуды ускорения воздействующего ударного импульса, но и соотношением длительности ударного импульса и периода собственных колебаний объекта (рис. 6.30). Большая величина отклика будет наблюдаться у конструктивных элементов, полупериод собственных колебаний которых сравним или меньше длительности ударного импульса. Другими словами, чем короче ударный процесс (меньше 
), тем меньшее число конструктивных элементов РЭС в максимальной степени будет реагировать на такое воздействие.
Этот вывод позволяет рекомендовать к использованию системы виброизоляции для защиты блоков РЭС и от ударных нагрузок, так как установка блоков на виброизоляторы приводит к увеличению значения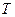 
(значение блока на виброизоляторах мало). При проектировании подобных систем виброизоляции следует иметь в виду то обстоятельство, что установка блока на слишком «мягкие», низкочастотные виброизоляторы может привести при ударной нагрузке к их деформации до упора и к потере эффективности такой защиты. Поэтому для защиты от ударных нагрузок рекомендуется использовать более жесткие, высокочастотные виброизоляторы, обеспечивающие при номинальной их нагрузке значения собственных частот систем виброизоляции в пределах 25... 30 Гц.
Рис. 6.30. Реакция конструктивного элемента или блока РЭС
при различных соотношениях длительности ударного импульса 
и периода собственных колебаний объекта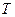
|
|
|
Оценить эффективность защиты блока на виброизоляторах от ударных нагрузок можно по следующей упрощенной методике, в соответствии с которой последовательно определяются динамические характеристики и параметры блока:
1. Частота собственных колебаний блока:
где 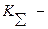суммарная жесткость виброизоляторов;
масса блока.
2. Условная частота воздействующего ударного процесса
где 
длительность ударного импульса.
3. Отношение частот
4. Коэффициент передачи удара (для полусинусоидального ударного импульса):
5. Ускорение блока в момент удара:
6. Максимальное значение смещения блока при ударе:
Защита от линейных нагрузок, которые характеризуются воздействием на РЭС и ее элементы инерционных сил, изменяющихся с течением времени достаточно медленно, сводится к увеличению прочностных свойств конструктивных элементов и их жесткости. Эти мероприятия, которые можно оценить методами технической механики при воздействии на объекты статических сил, предотвращают разрушение конструкций и недопустимые отклонения их частей от статического положения, что может привести к коротким замыканиям, соприкосновениям элементов и т.д.
Защита РЭС от акустических шумов обеспечивается конструкционным демпфированием (вибропоглощающие покрытия и слоистые конструкции для печатных плат) и использованием звукоизолирующих перегородок.
6.2.7. Защита РЭС при транспортировании
РЭС должны доставляться с завода-изготовителя к потребителю неповрежденными при транспортировании. Во время транспортирования и при проведении погрузочно-разгрузочных работ возможны ударные и вибрационные воздействия. Для защиты от подобных воздействий, климатических факторов, а также для сохранения товарного вида используется упаковка РЭС и их элементов.
Наиболее употребительное конструктивное исполнение упаковки включает достаточно жесткий внешний контейнер из картона или дерева и упаковочные прокладки между стенками контейнера и упаковываемым изделием (рис. 6.31).
Рис. 6.31. Упаковка РЭС:
1 – упаковываемое изделие; 2 – прокладка; 3 – внешний контейнер
В качестве материала для изготовления упаковочных прокладок используется пенополистирол, гофрированный картон, пенополиуретан, войлок и др. Основное требование к упаковочным материалам – малая жесткость или, другими словами, возможность относительно легкого деформирования под нагрузкой. Деформирование прокладки при ударе «растягивает» ударный процесс по времени и снижает уровень ударной нагрузки, действующей на упакованный аппарат (рис. 6.32).
Рис. 6.32. Ударные импульсы:
1 – для аппарата без упаковки; 2 – для аппарата в упаковке
Потенциальная энергия изделия в упаковке массой m, поднятого на высоту 
:
При ударе из-за смятия или деформации упаковки упакованное изделие проходит так называемый путь торможения 
. Если считать силу 
постоянной, то работа торможения
Приравняв эту работу к потенциальной энергии, получим:
Отношение 
показывает, насколько «увеличивается вес» упаковочной единицы за счет удара. Для снижения уровня динамических нагрузок на изделие это отношение уменьшают за счет увеличения , т.к. фиксировано. Конструкция упаковки это и обеспечивает. Если же упругость тары недостаточна, то в упаковке предусматривают дополнительные демпфирующие элементы.
В качестве примера на рис. 6.33 представлен вариант упаковки телевизионного приемника.
Рис. 6.33. Вариант выполнения упаковки:
1 – аппарат; 2 – упаковочная прокладка; 3 – картонная коробка
Как видно из рис. 6.33, упаковочные прокладки могут быть не сплошными по всем граням изделия, а, например, состоящими из двух профилированных накладок из пенополистирола, охватывающих только две грани упаковываемого аппарата. Остальные грани аппарата 1 защищены от возможных повреждений выступающими частями прокладок 2. Перед упаковкой аппарат может дополнительно помещаться в пакет из полиэтиленовой пленки.
Одна из методик расчета необходимой величины жесткости материала упаковки изложена в стандарте ФРГ [8].
Поясним суть этой методики на конкретном примере.
Задача
Дано: прибор массой 70 кг должен быть упакован так, чтобы максимальное значение возникающего ускорения не превышало 8 
при предполагаемой высоте падения = 0,4 м.
Определить необходимую жесткость упаковочного материала, величину максимального ускорения и собственную частоту прибора упаковке.
Решение
Для решения задачи используются две номограммы (рис. 6.34, 6.35).
Рис. 6.34. Номограмма для определения собственной частоты
Прибора в упаковке
Рис. 6.35. Номограмма для определения жесткости упаковки:
масса прибора, кг; собственная частота прибора в упаковке, Гц;
жесткость материала упаковки, Н/см
Используя рис. 6.34 по заданным значениям ускорения (j = 8 ) и предполагаемой высоты падения ( = 0,4 м), находим: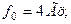 
Используя рис. 6.35, по найденной величине собственной частоты (
) и заданному значению массы прибора (
) находим необходимую для защиты прибора величину жесткости материала упаковки: 
6.2.8. Методы расчета конструкций с использованием ЭВМ
ЭВМ используются для проведения оценочных расчетов конструкций РЭС при механических воздействиях, например, для расчета систем виброизоляции. Вместе с тем есть методы расчетов, реализация которых без ЭВМ даже для решения простейших задач громоздка, а для расчетов сложных объектов вообще невозможна. К таким методам относят метод конечных элементов (МКЭ) и метод конечных разностей (МКР).
Метод конечных элементов широко используется в подсистемах прочностных расчетов современных САПР в авиационно-космической, судостроительной, строительной и других отраслях промышленности. Суть этого метода состоит в разбиении расчетной модели конструкции на конечные элементы, связанные в отдельных узловых точках. Затем формируются матрицы жесткостей [К], масс [М] и демпфирования [С] для отдельных конечных элементов модели и модели в целом, общий вектор силы {Р}. Математическая модель динамической системы может быть представлена системой дифференциальных уравнений второго порядка, которые в матричной форме имеют вид
В результате решения полученной системы уравнений определяют собственные частоты и формы колебаний конструкции, а также значения перемещения узлов 
.
При решении статических задач вышеприведенное уравнение упрощается и в общем случае имеет вид
Применительно же к конструкциям РЭС, где также в отдельных случаях возникает необходимость в проведении прочностных расчетов, в большей степени адаптирован метод конечных разностей, т.к. с его помощью можно решать и другие задачи, типичные для РЭС, например теплообменные.
Для реализации метода конечных разностей необходимо иметь математическую модель – дифференциальное уравнение, описывающее процессы, протекающие в конструкции. Суть метода состоит в записи исходного дифференциального уравнения в разностной форме и в решении его. В качестве примера рассмотрим функцию y = f (x) (рис. 6.36).
Рис. 6.36. Функция, зависящая от одной переменной
Первая производная для этой функции в разностной форме:
Вторая производная и производные более высокого порядка:
Для функции 
, зависящей от двух переменных х и у:
где 
шаг разбиения по осям х и у.
Покажем применение метода конечных разностей к прямоугольной пластине.
Дифференциальное уравнение, описывающее поведение пластины, имеет вид
где 
сила, действующая на пластину;
цилиндрическая жесткость пластины (см. п. 6.2.3).
Так как ранее были найдены значения производных, то окончательный вид уравнения в разностной форме для точки (рис. 6.37):
Рис. 6.37. Система координат и расчетные точки
Представим условно это выражение в виде вычислительного шаблона (рис. 6.38).
При анализе поведения пластин под нагрузкой возможны различные варианты закрепления ее сторон (различные варианты граничных условий).
Особенности вариантов закрепления сторон пластин учитываются введением фиктивных точек за пределами их контура (рис. 6.39).
|
Рис. 6.38. Вычислительный шаблон
Рис. 6.39. Учет граничных условий при различных вариантах
закрепления сторон пластин:
а – сторона пластины жестко защемлена; б – сторона пластины
находится на опоре
Рассмотрим реализацию метода конечных разностей на конкретном примере.
Задача
Квадратная плата с жестким защемлением сторон длиной а подвергается действию статической нагрузки Р 0. Найти прогибы платы от действия нагрузки.
Решение
Производим разбиение платы с шагом 
(рис. 6.40).
Рис. 6.40. Плата с расчетными точками 1, 2, 3
Как следует из рис. 6.40, достаточно найти прогибы платы в трех точках (
), а для остальных точек с теми же номерами прогибы будут одинаковы.
Совместив центр вычислительного шаблона с точкой 1, получим следующее распределение коэффициентов (рис. 6.41) и уравнение
Рис. 6.41. Распределение коэффициентов для точки 1
Совместив центр шаблона с точкой 2 (рис. 6.42), получаем второе уравнение:
Рис.6.42. Распределение коэффициентов для точки 2
Для точки 3 (рис. 6.43) получаем третье уравнение:
Рис. 6.43. Распределение коэффициентов для точки 3
В итоге получаем систему трех уравнений с тремя неизвестными 
:
.
Решая данную систему уравнений, получим:
Такая относительная простота использования МКР для решения практических задач исчезает при анализе объемных элементов конструкций, испытывающих действия динамических сил. Подобные задачи являются наиболее типичными при проектировании РЭС, предназначенных для эксплуатации на подвижных объектах. Используемые в этом случае уравнения теории упругости (уравнения Ламэ) имеют вид
и т.д. по остальным двум координатам,
где 
соответствующие перемещения в направлениях 
;
плотность материала;
и 
коэффициенты Ламэ.
Вторая производная по времени в правой части уравнения Ламэ в конечных разностях имеет вид
где шаг по времени.
Более сложный вид исходных дифференциальных уравнений, большее число узлов, появление еще одной переменной – времени, резко усложняет вычислительный процесс. Кроме того, при решении практических задач необходимо осуществить осреднение механических характеристик объекта, учесть потери энергии на внутреннее трение, граничные условия и т.д.
6.2.9. Общие рекомендации по защите РЭС от механических воздействий
Работа конструктора по обеспечению нормального функционирования РЭС в условиях воздействия вибраций начинается с сопоставления допустимых параметров вибраций для пассивных элементов аппаратуры (резисторы, конденсаторы и др.), транзисторы и микросхемы с требованиями технического задания на проектирование аппарата.
Если применяемые элементы удовлетворяют требованиям технического задания, то задача состоит в устранении резонансных колебаний конструктивных элементов (обеспечение режима, когда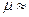 
1).
Если же используемые элементы не удовлетворяют требованиям технического задания или возможны резонансные колебания конструктивных элементов аппарата, то следует применять виброизоляцию (обеспечение режима ( < 1) с последующей оценкой ее эффективности.
Такой же подход при проектировании РЭС рекомендуется применять и для других видов механических воздействий – ударов, линейных нагрузок, акустических шумов.
Приведем пример оценочного расчета РЭС с учетом механических воздействий.
Задача
Блок массой 6 кг установлен на четырех виброизоляторах (нижний монтаж), жесткость каждого из которых 
= 2 Н/мм. Внутри блока параллельно его основанию жестко по контуру закреплена печатная плата из стеклотекстолита (
; 
=0,52; =0,06). Размеры платы 200 · 100 · 1 мм. Масса ЭРЭ и ИМС, размещенных на поверхности платы, составляет 60 г. Амплитуда и частотный диапазон воздействующей на блок вибрации: 
= 10 мм; 
= 40 Гц; 
= 80 Гц. Определить возможность использования в составе конструкции элемента, размещенного на поверхности платы, если его собственная частота 
= 2 кГц, а допустимая величина вибрационной нагрузки 
= 10g.
Решение
1. Поставленную задачу представим в виде следующей физической модели (рис. 6.44).
Рис. 6.44. Модель по условию задачи
2. Определим динамические характеристики составляющих модель элементов:
а) собственная частота блока на виброизоляторах
б) собственная частота печатной платы
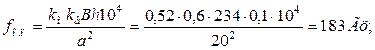
в) собственная частота элемента
(по условию задачи).
3. Определим амплитуду колебаний блока на границах диапазона частот воздействующих вибраций:
где 
мм;
мм.
Эти величины амплитуд являются базовыми для оценки динамического состояния печатной платы.
4. Определим амплитуды колебаний центра платы на границах диапазона частот воздействующих вибраций:
В общем случае
но так как в нашем случае значение платы в несколько раз превышает значение частот воздействующих вибраций и ввиду малости , можно принять .
Тогда
мм;
мм.
5. Определим величину вибрационной нагрузки в центре платы на границах диапазона частот воздействующих вибраций:
g;
g.
Сравниваем полученные значения вибрационной нагрузки с допустимой условиям задачи (jдоп = 10 g) и делаем вывод о возможности использования элемента в составе данной конструкции.
|
|
|
