 |
Методы для угловых и линейных измерений.
|
|
|
|
Измерение углов выполняют способом круговых приемов или способом измерение отдельного угла. Для ослабления влияния погрешностей центровок и редукций полигонометрии применяют трехштативную систему измерения углов.
Способ круговых приемов. Способ применяется тогда, когда на пункте
полигонометрии имеется больше двух направлений. Способ круговых приемов позволяет выразить результаты наблюдений в виде измеренных направлений, т.е. отсчетов, взятых по неподвижному лимбу при визировании на все наблюдаемые пункты. Эти данные позволяют рассчитать любой из углов между направлениями на наблюдаемые пункты как разность измеренных направлений.
Если это исходный пункт. Пусть будет более двух направлений, А и В, тогда одно из направлений выбирается наблюдателем за начальное, например OA. При КL наводят теодолит на А и устанавливают по лимбу отсчёт близким к нулю, отсчёт берут дважды (по барабанчику микрометра). Затем вращают теодолит по часовой стрелке берут отсчёт на B,C,D,A. Повторное наблюдение начального направление (на пункт А) называется замыканием горизонта и служит для контроля неподвижности лимба в течении полуприема. Величина незамыкания горизонта не должна превышать двойной точности отсчетного устройства теодолита 0.2 ' для теодолитов Т5 и 8" - для Т2 и аналогичных им по точности приборов. При больших расхождениях весь полуприем повторяют заново. Затем против часовой стрелки, то есть ё обратном направлении при КП A,D,C,B,A. Эти действия составлякгг один приём. Число приёмов зависит от класса, разряда и от прибора. Например: в полигонометрии первого разряда теодолитом 2Т2 углы надо измерять двумя приёмами.
Способ отдельного угла. Применяют тогда, когда на пункте два направления(все точки, кроме узловых и исходных).Наблюдения выполняют вращая в каждом полуприёме алидаду только в одном направлении (по часовой стрелке).В этом способе не выполняют замыкания горизонта.
|
|
|
| А |
| В |
< К Л = В-А;
< КП = А-В
Кроме этого, в приёме вращения теодолита производят по часовой или против часовой.
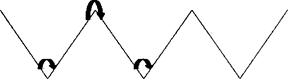
Трехштативная система.
В качестве визирных целей используют специальные марки.
И теодолит и марки при закреплениях закреплены в подставки. Подставки закрепляются на штативах. При измерениях как прибор, так и визирная цель должны быть установлены точно над центрами пунктов, то есть оси марок и теодолита должны проектироваться в центр пункта. Сначала мерим угол ABC. Над пунктами устанавливаем штативы с закреплёнными на них подставками (без теодолита). С помощью оптических центров. В подставки точек А и С ставятся марки, в точку В - теодолит, затем задний штатив переносят с А на D и центрируют. Не трогая штатив с подставкой в точке В и С, вынимаем теодолит и марку, и меняем их местами.
А С
|
В D
В работе мы используем способ круговых приемов и способ отдельного
угла.
Измерение линий светодальномером
Предположим, что в некоторый момент времени Т1 передатчик, расположенный в пункте А получает в направлении к пункту В электромагнитные волны в виде отдельного импульса (т.е. прерывисто), который затем отражается и в момент времени Т2 приходит обратно в пункт А. Измерив промежуток времени Т2-Т1 и зная скорость распространения эл.м. волн v, можно подсчитать расстояние D между пунктами А и В, предполагая при этом, что эл.м. Волны распространяются прямолинейно: 2D=v(T2-Tl), откуда D=v*Г/2, где Г - время распространения эл.м. волн, равное Т2-Т1. Следовательно, установив на одном конце линии приёмопередатчик, излучающий и принимающий эл.м. волны, а так же устройства для измерения времени распространения этих волн, а на другом отражатель, можно определить расстояние D. Такое устройство, состоящее из двух частей, называется дальномером.
|
|
|
ТЕОРИЯ ОШИБОК И УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ
ТЕОРИЯ ОШИБОК
А. Равноточные измерения
Виды ошибок измерения. Любые измерения сопровождаются ошибками. Ошибки зависят от многих причин, в первую очередь от несовершенства применяемых инструментов, от несовершенства органов чувств наблюдателя и от конкретных условий, в которых производятся измерения.
Различают три основных вида ошибок: грубые ошибки или промахи, систематические ошибки и случайные (неизбежные) ошибки.
Грубые ошибки или промахи. Грубые ошибки недопустимы при производстве измерений, так как они «могут весьма значительно исказить результаты измерений. Чаще всего эти ошибки вызваны небрежностью, просчетом наблюдателя (просчет целой ленты при измерении длин, просчет десятков минут или градусов при измерении углов и т. д.). Грубые ошибки могут быть вызваны также неисправностью инструмента или небрежностью при обращении с ним (не закреплен становой винт теодолита при измерении углов, не приведен на нульпункт пузырек уровня при измерении вертикальных углов и т. д.).
При правильной организации измерений грубые ошибки не должны иметь места.
Основным методом выявления грубых ошибок служат контрольные измерения. Результаты измерения, содержащие грубые ошибки, отбрасываются и измерения повторяются вновь. Методика производства измерений, разрабатываемая в специальных курсах — маркшейдерское дело, геодезия, горная геометрия и т. д. — в первую очередь предусматривает возможность выявления грубых ошибок. В теории ошибок грубые ошибки или промахи не рассматриваются.
Систематические ошибки. При производстве данного измерения систематические ошибки остаются постоянными по величине и по знаку или изменяются по определенному закону. Абсолютная величина и знак систематической ошибки могут быть выражены в виде однозначной функции от условий измерения и соотношения отдельных элементов измерительного инструмента. К систематическим ошибкам относятся, например, несовпадение номинальной длины мерной ленты с ее фактической длиной (ошибка компарирования ленты), изменение длины ленты при изменении температуры, ряд инструментальных ошибок, например влияние негоризонтальности оси вращения трубы теодолита при измерении горизонтальных углов в наклонных выработках и т. п. К систематическим ошибкам могут быть отнесены также личные ошибки наблюдателя.
|
|
|
Систематические ошибки, так же как и грубые ошибки, должны быть исключены из результатов измерения. В отличие от грубых ошибок, они практически не могут быть исключены полностью, а только в пределах необходимой и достаточной точности. Методы исключения из результатов измерения систематических ошибок следующие:
1) определение величины и знака систематической ошибки и исправление результата измерения путем введения соответствующей поправки;
2) использование такой организации измерений, при которой систематическая ошибка исключается в процессе наблюдения (отсчет по двум нониусам теодолита для исключения ошибки, вызываемой эксцентриситетом алидады, и т. п.). Методы определения систематических ошибок и конкретная методика измерения для исключения систематических ошибок разрабатываются соответствующими специальными дисциплинами, и в теории ошибок не рассматриваются.
Случайные ошибки. Случайные ошибки органически присущи измерениям. Полностью исключить их из результатов измерения и практически и принципиально невозможно. Поэтому иногда они называются неизбежными ошибками. Изменяя методику, инструменты и условия измерения, можно уменьшить величину случайных ошибок, а принципиально возможно сделать их по абсолютному значению меньше любого наперед заданного значения. В соответствии с проводимыми измерениями различают случайные ошибки отдельных измерительных операций, например, при измерении угла теодолитом — случайные ошибки визирования, отсчета по лимбу, центрирования инструмента и т. д. или в целом всего измерительного действия — случайная ошибка измерения угла. Теория ошибок рассматривает, в основном, только случайные ошибки.
|
|
|
К случайным ошибкам относятся ошибки, обладающие следующим основным свойством. Появление при ряде измерений ошибок 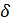 , равных по величине и обратных по знаку, — равновероятно. Как следствие, получаем:
, равных по величине и обратных по знаку, — равновероятно. Как следствие, получаем:
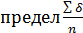 =
= 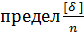 = 0 при n
= 0 при n 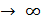 .
.
где n — число отдельных случайных ошибок равноточных независимых измерений одной и той же измеряемой величины, безошибочное значение которой известно;
 — случайная ошибка, получаемая как разность между безошибочным значением и измеренным значением измеряемой величины.
— случайная ошибка, получаемая как разность между безошибочным значением и измеренным значением измеряемой величины.
В отличие от грубых и систематических ошибок при производстве измерений нельзя определить или вычислить величину и знак случайной ошибки 8, за исключением того случая, когда известно безошибочное или «истинное» значение измеряемой величины. Если результаты измерений по
кажут, что — не стремится к нулю при увеличении числа измерений я,
то это будет 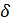 свидетельствовать о наличии систематических ошибок в измерениях.
свидетельствовать о наличии систематических ошибок в измерениях.
Средняя квадратическая ошибка. За меру случайных ошибок чаще всего принимают среднее квадратическое из отдельных случайных ошибок независимых равноточных измерений, которое называют средней квадратической ошибкой или, сокращенно, средней ошибкой. Средняя ошибка m выражается формулой
m = 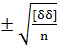
где [  =
= 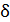 12 +
12 + 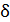 22 +
22 +  +
+ 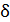 n2
n2
n — число отдельных случайных ошибок 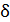 равноточных независимых измерений одной и той же измеряемой величины, безошибочное значение которой известно.
равноточных независимых измерений одной и той же измеряемой величины, безошибочное значение которой известно.
Для вычисления средней ошибки по приведенной формуле необходимо знать безошибочные значения измеряемых величин, так как случайные ошибки 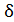 представляют разность между безошибочным значением и измеренным значением измеряемой величины. Применять эту формулу удается весьма редко, так как почти всегда неизвестны безошибочные значения измеряемых величин1
представляют разность между безошибочным значением и измеренным значением измеряемой величины. Применять эту формулу удается весьма редко, так как почти всегда неизвестны безошибочные значения измеряемых величин1
1 Под вероятностью w понимается отношение а — числа случаев, благоприятствующих появлению данного события, к N — общему числу всех возможных случаев:
 =
= 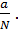
Вероятность, равная 1 (при a = N), свидетельствует о достоверности появления рассматриваемого события. Вероятность, равная 0, свидетельствует о невозможности появления рассматриваемого события.
Вычисление средней квадратической ошибки равноточно измеренных величин. На практике чаще всего среднюю ошибку вычисляют по отклонениям измеренных значений от наиболее вероятных значений измеряемых величин. В этом случае средняя ошибка измерения m выражается формулой
m = 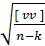 =
= 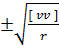 ,
,
где v — отклонение измеренных значений от наиболее вероятных значений измеряемых величин; г — число избыточных (лишних) измерений, равное разности между числом всех произведенных измерений — n и числом необходимых измерений — k (необходимых для однократного получения значений всех измеряемых величин). Под наиболее вероятным значением измеряемых величин понимаются их значения, полученные в результате уравнения по способу наименьших квадратов (по принципу наибольшего веса).
|
|
|
Разность v между измеренным значением и наиболее вероятным значением называется вероятнейшей ошибкой. Таким образом, можно сказать, что средняя ошибка равна корню квадратному из суммы квадратов вероятнейших ошибок, деленной на число избыточных измерений.
Для случая, когда n раз равноточно измерена одна и та же величина, уравнивание измерений сводится к взятию среднего арифметического из измеренных значений и средняя ошибка измерения будет вычисляться по формуле
m = 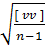
| так как число необходимых измерений в данном случае равно единице. Для этого случая сумма вероятнейших ошибок всегда будет равна нулю: |
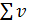 = v 1 + v2 +
= v 1 + v2 +  + vn = 0
+ vn = 0
что может служить контролем вычисления вероятнейших ошибок и среднего арифметического измеряемой величины.
Средняя ошибка уравненных значений измеряемых величин. При равноточных измерениях средняя ошибка уравненных (по способу наименьших квадратов) значений М равна средней ошибке измерений т, умноженной на корень квадратный из числа необходимых измерений k, деленного на число всех измерений п:
M =  m
m 
Средняя ошибка среднего арифметического. Если n раз равноточно измеряется одна и та же величина, то уравнивание измерений сводится к взятию среднего арифметического из измеренных значений. Для этого случая средняя ошибка уравненного значения измеряемой величины, называемая средней ошибкой среднего арифметического М, будет равна
M =  m
m  =
= 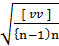 =
= 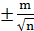 ,
,
| так как число необходимых измерении k для данного случая равно единице. Связь между средней и одиночной ошибками. В практике работ, по результатам измерения при наличии избыточных измерений можно вычислить среднюю ошибку по вероятнейшим ошибкам (поправкам), не зная |
одиночных случайных ошибок. Возникает вопрос, как, зная среднюю ошибку, перейти к случайной ошибке отдельной измеряемой величины или отдельного измерения. Случайная ошибка отдельного измерения может иметь как положительный, так и отрицательный знак, а по абсолютному значению может быть и меньше и больше средней ошибки.
Используя теорию вероятностей, можно установить следующее. Появление случайной ошибки отдельного измерения как со знаком плюс, так и со знаком минус равновероятно. Вероятность1 того, что случайная ошибка отдельного измерения будет по абсолютному значению меньше средней ошибки, равна примерно 2/з, а вероятность того, что она будет больше средней ошибки, равна примерно !/з
Чем больше значение случайной ошибки отдельного измерения, тем меньше вероятность ее появления при прочих равных условиях. Так, например, вероятность появления отдельной случайной ошибки по абсолютному значению большей средней ошибки равна '/з, большей двукратной средней ошибки — 1/22, большей трехкратной средней ошибки — 1/370, большей четырехкратной средней ошибки — 1/15800 и большей пятикратной средней ошибки —1/1 740 000.
Вероятность появления случайной ошибки, лежащей в пределах от
— km до + km, или, что то же, лежащей по абсолютному значению в пределах от нуля до 6-кратной средней ошибке, может быть вычислена по формуле:
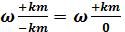 = k
= k 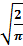 (1 -
(1 -  +
+ 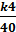 -
- 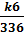 +
+  +
+  ).
).
Для этой же цели может быть использована приводимая ниже таблица, содержащая значение вероятности появления случайной ошибки по
| Предельная ошибка.За предельную ошибку принимается такое значение случайной ошибки, возникновение ошибок больше которого практически мало вероятно.Обычно предельную ошибку mпред выражают величиной, кратной средней ошибке, mпред. = K m, где k – коэффициент кратности, m – средняя ошибка. |
1 Под вероятностью w понимается отношение а — числа случаев, благоприятствующих появлению данного события, к N — общему числу всех возможных случаев:
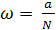 .
Вероятность, равная 1 (при a= N), свидетельствует о достоверности появления рассматриваемого события. Вероятность, равная 0, свидетельствует о невозможности появления рассматриваемого события. .
Вероятность, равная 1 (при a= N), свидетельствует о достоверности появления рассматриваемого события. Вероятность, равная 0, свидетельствует о невозможности появления рассматриваемого события.
|
абсолютному значению большей km (табл. 1).
Таблица 1
|
При принятии за предельную ошибку того или иного значения всегда остается возможность появления случайной ошибки больше принимаемой предельной ошибки. Очевидно, чем большее принять значение k, тем меньше будет вероятность появления ошибки больше предельной. Принимая за предельную ошибку 2т — удвоенную среднюю ошибку, можно ожидать, что в одном случае из 22 наблюдаемых случаев ошибка будет больше принимаемой предельной. Здесь степень риска, очевидно, сравнительно большая. Принимая за предельную ошибку пятикратную среднюю ошибку — 5m, можно ожидать, что только в одном случае из 1 740 000 может появиться случайная ошибка по абсолютной величине больше предельной. Очевидно, вероятность появления ошибки по абсолютному значению большей пятикратной средней ошибки весьма ничтожна, и вряд ли есть основание принимать за предельную ошибку пятикратную среднюю ошибку.
Вероятность появления случайных ошибок, по абсолютному значению превышающих величину принимаемой предельной ошибки, можно вычислить при помощи таблицы, приведенной в предыдущем параграфе (см. табл. 1), Так, если за предельную ошибку принята двукратная средняя ошибка (коэффициент кратности k=2), то вероятность 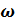 появления случайных ошибок по абсолютной величине больших принятой предельной ошибки найдем по таблице; для k = 2,0 имеем (
появления случайных ошибок по абсолютной величине больших принятой предельной ошибки найдем по таблице; для k = 2,0 имеем ( 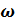 )2m0 = 0,0455, или это будет составлять 4,55 случая из 100 случаев, или примерно 1 случай из 22 случаев
)2m0 = 0,0455, или это будет составлять 4,55 случая из 100 случаев, или примерно 1 случай из 22 случаев
(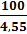 ~ 22). Если за предельную ошибку принять трехкратную среднюю ошибку, то, соответственно, по таблице получим для k = 3,0 значение вероятности(w) 3 0m = 0,0027, что доставит один случай из 370 случаев
~ 22). Если за предельную ошибку принять трехкратную среднюю ошибку, то, соответственно, по таблице получим для k = 3,0 значение вероятности(w) 3 0m = 0,0027, что доставит один случай из 370 случаев
(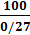 ~ 370).
~ 370).
За предельную допускаемую ошибку или невязку при производстве маркшейдерских и топографическо-геодезических работ обычно принимается двукратная средняя ошибка mпред — 2 т. Вероятность появления фактической ошибки большей двукратной средней составляет 0,0455, или 4,55%. Таким образом, принимая за предельную допускаемую ошибку двукратную среднюю ошибку, мы рискуем напрасно забраковать 4,55% работ, выполненных с требуемой точностью — с заданной средней ошибкой m. В то же время, если фактические невязки и не будут превышать допустимые невязки (двукратных средних), но по своей абсолютной величине большинство из них будет приближаться к предельным допустимым, то это будет свидетельствовать о недостаточной точности производства работ и о необходимости более тщательно производить измерения. Распределение фактических ошибок (невязок) по абсолютной величине, при значительном количестве их, должно примерно соответствовать табл. 2.
При решении специальных задач за предельную ожидаемую ошибку при предрасчете точности, производимом для определения методики работ и выбора необходимых инструментов, обычно принимается утроенная средняя ошибка — 3 m.
При этом необходимо учитывать, что, принимая за предельную ожидаемую ошибку утроенную среднюю, мы допускаем риск в 0,3%, т. е. в трех случаях из тысячи. При предрасчете точности особо ответственных работ за предельную ожидаемую ошибку обычно принимается учетверенная средняя
ошибка, в этом случае риск снижается до 0,006%, т. е. до одного случая из
16 000.
Таблица 2
| Абсолютные значения ошибок - -невязок | Число ошибок (невязок)из 100 случаев |
| От 0 до 0,5 m | |
| От 0 до 1 m | |
| От 0 до 1,5 m | |
| От 0 до 2,0 m | |
| Свыше 2m | |
| От 0 до 3,0 m | 3 из 1000 |
| m – средняя квадратическая ошибка |
С р е д няя а р и ф м е т и ч е с к а я ошибка. Для оценки точности произведенных измерений наряду со средней квадратической ошибкой m. иногда применяется, средняя арифметическая ошибка t. Средней арифметической ошибкой t называется среднее арифметическое из абсолютных значений случайных ошибок  :
:
t = 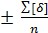 ,
,
где 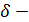 разность между безошибочным значением и измеренным значением юмеряемой величины;
разность между безошибочным значением и измеренным значением юмеряемой величины;
n — число случайных ошибок, что соответствует числу измерений. Среднюю арифметическую ошибку можно вычислить и по значениям
вероятнейших ошибок v, пользуясь формулой
t = 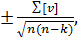
где v — разность между наиболее вероятным и измеренным значением
измеряемой величины;
n —чиcло вероятнейших ошибок, равное числу всех измерений;
k - число необходимых измерений;
(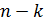 )— число избыточных (лишних) измерений.
)— число избыточных (лишних) измерений.
Вероятность появления случайной ошибки по абсолютному значению большей средней арифметической равна 0,5751.
Вероятная ошибка. Наряду со средней квадратической ошибкой m и со средней арифметической ошибкой t, для оценки точности произведенных измерений иногда применяется вероятная ошибка р. Вероятной ошибкой называется такое значение ошибки, вероятность появления случайной ошибки по абсолютному значению больше или меньше которого равна 1/2, т. е. равновероятно появление случайной ошибки по абсолютному значению больше или меньше вероятной ошибки. Вероятная ошибка по результатам измерений непосредственно не вычисляется, а выражается через среднюю квадратическую или среднюю арифметическую ошибку.
Связь между средней квадратической, средней арифметической и вероятной ошибками. Значения средней квадратической ошибки m, средней арифметической ошибки t и вероятной ошибки р связаны между собой. Эту связь с практически достаточной точностью можно выразить следующими равенствами:
| m=1,25t =1,48p |
t = 0,80m= 1,18 p
p= 0,674m =0,845t.
Приведенные равенства справедливы только при большом числе случайных ошибок  , практически при числе ошибок, большем 10—15.
, практически при числе ошибок, большем 10—15.
Ошибка средней ошибки. Средняя квадратическая ошибка m вычисляется как корень квадратный из суммы квадратов вероятнейших ошибок [vv], деленной на число избыточных измерений г (см. выше, стр. 79). Чем больше число избыточных измерений г, тем точнее получается значение средней квадратической ошибки. Отсюда можно поставить вопрос о средней квадратической погрешности m(m) средней квадратической ошибки m, вычисленной по небольшому числу вероятнейших ошибок. С практически достаточной точностью среднюю квадратическую погрешность средней квадратической ошибки можно
m(m) = 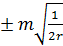 =
= 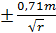 .
.
Таким образом, при одном избыточном измерении средняя квадратическая ошибка определяется сама со средней ошибкой порядка 71%, при двух избыточных измерениях — с ошибкой порядка 50%, при 10 избыточных измерениях — с ошибкой порядка 23% и т. д. Отсюда следует, что значения средних квадратических ошибок, как правило, вполне достаточно вычислять с двумя значащими цифрами. Средняя квадратическая ошибка средней арифметической ошибки т (t) в процентном отношении несколько больше, чем средняя квадратическая ошибка средней квадратической ошибки т (т). Отсюда следует, что при ограниченном числе избыточных измерений средняя квадратическая ошибка m лучше характеризует точность измерений, чем средняя арифметическая ошибка t. квадратической ошибки получено при решении примера 1, с меньшей затратой труда значение средней квадратической ошибки получено при решении примера 2.
Пример 3. Измерена два раза равноточно длина одной и той же стороны теодолитного хода. Получены значения:
l1 = 54,745; l2= 54,737.
Найти среднюю ошибку измерения m и среднюю ошибку наиболее вероятного значения измеряемой длины М.
Решение. Наиболее вероятное значение измеряемой длины L получится как среднее арифметическое из равноточных измерений
L = 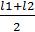 = 54,7 +
= 54,7 + 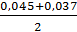 = 54,741.
= 54,741.
Вычисление вероятнейших ошибок измерения v:
V1=l1-L = = 54,745 — 54,741 = + 0,004;
v 2 = l 2 — L = 54,737 — 54,741 = — 0,004.
Контроль вычисления L и v:
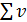 = v1+v2= + 0,004 — 0,004 = 0.
= v1+v2= + 0,004 — 0,004 = 0.
Вычисление средней ошибки измерения m.:
m = 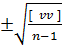 =
=  0,001
0,001  =
= 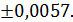
Вычисление средней ошибки наиболее вероятного (уравненного)
значения М,
M = 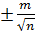 =
= 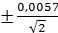 =
=  0,0040.
0,0040.
Эту же задачу можно решить иначе, используя разность двойных равноточных измерений d
d=l1 — l2 = 54,745 — 54,737 =  0,008.
0,008.
Вычисление средней ошибки измерения ш:
m = 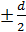 =
= 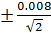 =
=  0,0057.
0,0057.
Вычисление средней ошибки уравненного значения М\ m M =  =
= 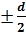 =
= 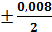 =
=  0,004.
0,004.
П р и м е р За. Если иметь несколько разностей двойных равноточных измерений одной и той же или нескольких однородных величин, то среднюю ошибку таких измерений можно вычислить по формуле
m =  ,
,
где d — разность двойных равноточных измерений;
п — число двойных равноточных измерений или число разностей.
d1=  4"; d2 = ± 6"; d3=± 2";
4"; d2 = ± 6"; d3=± 2";
m = ± 
Если каждая пара измерений выполнена равноточно, но измерения различных пар не равноточны, то средняя ошибка измерения с весом р = 1 будет вычисляться по формуле
m = 
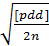 ,
,
где p1, р2,...,рn — веса пар равноточных измерений.
d1 = 8 см, р 1=l; d2= 12 см, р 2 = 1,5; d3= 10 см, р3 = 0,5.
m0 = 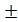
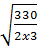 =
=  7,5 c
7,5 c
Пример 4, Измерены равноточно углы теодолитного хода. Средняя квадратическая ошибка измерения углов теодолитного хода т =  15"-
15"-
Найти: а) вероятность того, что случайная ошибка о измерения одного из углов теодолитного хода превысит; 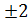 1",
1",
б) вероятность того, что случайная ошибка 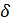 измерения одного из углов теодолитного хода превысит
измерения одного из углов теодолитного хода превысит  36".
36".
Решение, а) Вычисление коэффициента кратности k;
K = 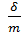 =
= 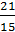 =1,4.
=1,4.
Используя табл. 1, находим вероятность появления случайной ошибки по абсолютному значению большей km.
При k= 1,4
w = 0,1615 =  .
.
Таким образом, вероятность появления фактической ошибки измерения угла в +21" при средней квадратической ошибке измерения углов  15" составляет 0,1615 или 16%, что соответствует одному случаю из шести случаев.
15" составляет 0,1615 или 16%, что соответствует одному случаю из шести случаев.
б) Вычисление коэффициента кратности:
k = 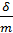 =
=  =2,4.
=2,4.
Используя табл. 1, находим вероятность появления случайной ошибки по абсолютному значению большей km.
При k= 2,4
w = 0,0164 = 1,6% =  .
.
Таким образом, появление фактической ошибки измерения угла в  36" при средней квадратической ошибке измерения углов m =
36" при средней квадратической ошибке измерения углов m =  15" составляет 0,164 или 1,6%, что соответствует одному случаю из 61 случая.
15" составляет 0,164 или 1,6%, что соответствует одному случаю из 61 случая.
Пример 5. Нужно обеспечить с вероятностью 1: 1000, чтобы 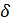 — ошибка измерения каждого из углов теодолитного хода не была больше + 30".
— ошибка измерения каждого из углов теодолитного хода не была больше + 30".
Найти, с какой средней квадратической ошибкой m необходимо измерять углы теодолитного хода.
Решение. Нахождение коэффициента кратности k для вероятности 0,001 производится по табл. 1.
В таблице имеем: при вероятности 0,0014 k = 3,2, при вероятности 0,0007
k = 3,4. Интерполяцией получаем для вероятности 0,001 k = 3,3.
Затем вычисляем среднюю квадратическую ошибку m:
m =  =
=  =
= 
Таким образом, для того, чтобы ошибка измерения каждого из углов теодолитного хода с вероятностью одна тысячная не превзошла величины
 30", углы теодолитного хода необходимо измерять по методике, рассчитанной на среднюю квадратическую ошибку измерения m =
30", углы теодолитного хода необходимо измерять по методике, рассчитанной на среднюю квадратическую ошибку измерения m =  9".
9".
Пример 6. Одним и тем же наблюдателем, одним и тем же инструментом и при одинаковых условиях измерено пять углов теодолитного хода. Каждый угол измерялся независимо два раза. По разности двойных измерений вычислены средние квадратические ошибки:
m1= ± 5"; m2 = ± 15"; m3 = ± 27"; m4 = ± 10"; m5 = ± 20".
Найти среднюю квадратическую ошибку измерения углов теодолитного хода mcр и определить, можно ли считать равноточными произведенные, измерения углов.
Решение. Вычисление средней квадратической ошибки измерения углов теодолитного хода mcр (принимая произведенные измерения углов равноточными):
mcp = ± 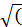 m21 + m22 + m23 + m24 + m25) / 5
m21 + m22 + m23 + m24 + m25) / 5
mcp = ±  (52 + 152 + 272 + 102 + 202) / 5 = ± 17”.
(52 + 152 + 272 + 102 + 202) / 5 = ± 17”.
Вычисление средней квадратической погрешности m (m) средней квадратической ошибки т, полученной по разности двойных измерений (число избыточных измерений г = 1, необходимо измерить угол один раз, а измерялся каждый угол два раза):
m(m) = ± 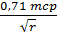 = ±
= ±  = ± 12”.
= ± 12”.
Значения средних квадратических ошибок m1, m2,m3, m4, m5 отличаются от значения mcp в пределах 2т (т) = + 12", 2 = + 24". Следовательно, нет оснований считать произведенные измерения углов нерaвноточными.
Вычисление средней квадратической погрешности средней квадратической ошибки измерения углов теодолитного хода т (mср):
m(mcp) = ± 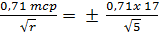 =
=  5”.
5”.
Пример 7. По расчету получено, что при принятом методе работ средняя квадратическая ошибка сбойки, зависящая от ошибок измерения углов, в интересующем направлении тр =  15 см. При этом принималось, что средняя квадратическая ошибка измерения углов m =
15 см. При этом принималось, что средняя квадратическая ошибка измерения углов m =  30".
30".
Найти, с какой точностью (средней квадратической ошибкой тн ) необходимо измерять углы, чтобы с вероятностью w = 0,005 (один случай из 200 случаев) случайная ошибка сбойки 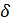 не превзошла величины + 10 сл.
не превзошла величины + 10 сл.
Решение. Нахождение коэффициента краткости k, соответствующего вероятности появления случайной ошибки по абсолютному значению большей km производится по табл. 1.
При w = 0,005 к = 2,8.
Вычисление необходимой точности измерения углов, обеспечивающей с вероятностью 0,005. что ошибка сбойки не превзойдет  15 см:
15 см:
mн.15 = 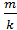 =
= 
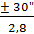 =
=  11”.
11”.
Вычисления необходимой точности измерения углов (средней квадратической ошибки mн), обеспечивающей с вероятностью 0,005, что ошибка сбойки не превзойдет 10 см:
mн = 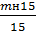 10 =
10 =  10 =
10 = 
Пример 8. Имеем двенадцать равноточно измеренных величин n =12; для определения всех искомых элементов необходимо измерить восемь величин k = 8. В результате уравнивания по способу наименьших квадратов (методом условных уравнений или методом косвенных наблюдений безразлично) получены наиболее вероятные значения поправок к измеренным величинам.
Сумма квадратов поправок= 124,36.
Найти среднюю квадратическую ошибку измерения m и среднюю
квадратическую ошибку уравненных значений М.
Решение. Вычисление средней квадратической ошибки измерения т:
Так как вероятнейшие ошибки по а
|
|
|


