Б. Неравноточные измерения

Понятие о весах. При совместном уравнивании неравноточно из­меренных величин необходимо знать средние ошибки этих измеренных вели­чин. Для упрощения действий при совместном уравнивании неравноточных величин вводится понятие — вес. Весом р называется величина, обратно про­порциональная квадрату средней ошибки.

Если имеем значения неличин l_1, 1₂, средние ошибки этих зна­чений, соответственно, m²₁, m²₂,...,m²_п. то весами величин l₁, 1₂,..., назы­ваются числа р, удовлетворяющие равенствам:

P₁= A/, m²_1; р_{2 =} A/, m²₂ ; 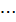р_{n =} A/, m²_n.

где А - произвольное, постоянное число.

Для вычисления весов числу А можно придать любое, произвольное значение, но обязательно одно и то же значение при вычислении весов совместно используемых (уравниваемых) величин. Так же и средние ошибки m₁, m₂,...,m_n совместно уравниваемых однородных величин должны выра­жаться в одних и тех же единицах измерения.

Например, при уравнивании углов средние ошибки всех углов должны быть выражены или в секундах, или в минутах и т. д.; при уравнивания длин средние ошибки всех длин должны быть выражены или в метрах, пли в сантиметрах и т. д.

Веса в извесной мере характеризуют точность измерений, так как чем больше вес, тем точнее известна величина по отношению к другим сов­местно уравниваемым однородным величинам. Если вес p_t измерения в а раз больше веса р₂ измерения l₂, то средняя ошибка m₁ измеренияl₁в меньше средней ошибки т₂ измерения 1₂.

Если р_{1 =} а р_2, то m_{1 =}

Иногда, не зная средних ошибок неравноточно измеренных величин, можно определить веса этих измеренных величин. Например, измерены два угла l₁ и l₂. Уголl₁ измерен один раз одним круговым приемом, угод 1₂ измерен два раза независимо, каждый раз одним круговым приемом тем же инструментом и при тех же условиях. За измеренное значение угла 1₂ при­нято среднее арифметическое из двух приемов. Тогда вес угла 1₂ будет в два раза больше, чем вес угла l₁ так как средняя ошибка т₂ угла 1₂ в раз меньше, чем средняя ошибка т₁ углаl₁.

Если т₂ = то p₂ = ap₁.

Вычисление средней квадратической ошибки при неравноточных измерениях. Если дано n неравноточно измерен­ных величинl₁ , l₂…. l_{n п} и веса этих измерений соответственно равны p₁, p₂….p_nто при совместном уравнивании можно вычислить средние ошибки измерений l₁,l₂, ….. ln.. Средняя квадратическая ошибка m_i измерения с весом Pi по результатам совместного уравнивания вычисляется по фор­муле

mi = = .

где v—вероятнейшие ошибки измерений, равные по абсолютному значе­нию поправкам, полученным в результате строгого уравнивания;

n — число всех измеренных величин;

k — число необходимых измерений;

г — число избыточных измерений, г = nп — k,

р — веса измеренных величин;

pi—вес измерения, средняя ошибка которого вычисляется

[ pvv] = p₁v²₁ + p₂v²₂ =…. p₂nv²_n.

Для упрощения вычислений вводится понятие — средняя квадратиче­ская ошибка единицы веса m₀, т. е. средняя ошибка такого измерения, фактически может быть и не производившегося, вес которого равен единице

m_{0 =}

Ошибка т₀ является величиной не именованной (не имеющей размерности).

Вычисление средней квадратической ошибки mi измерения с весом рi используя среднюю квадратическую ошибку единицы веса т₀, производят по формуле mi _{= =}

Для случая, когда n раз неравноточно измерена одна и та же величина, уравнивание измерений сводится к взятию общего арифметического сред­него (или, что то же, весового среднего, или общей арифметической сере­дины) из измеренных значений, и ошибка единицы веса будет вычисляться по формуле

m_{0 =}

 

а ошибка весового среднего будет вычисляться по формуле

mi _{= =}

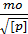
Для этого случая сумма произведений из вероятнейших ошибок v на соответствующие веса р всегда будет равна нулю..

[pv] = p ₁v₁ + p₂v₂ + …. p_nv_n = 0.

Это может служить контролем вычисления вероятнейших ошибок и кон­тролем вычисления весового среднего.

Неоднородные измерения. При строгом совместном уравнива­нии разнородных измеренных величин, например измеренных длин и углов при уравнивании полигонометрических ходов, неизбежно встает вопрос о вы­числении весов измеренных величин. Разнородные величины по существу не могут быть измерены равноточно уже в силу того, что они разнородны, т. е. измеряются в несравнимых единицах (например, длины измеряются в метрах, сантиметрах и т. д., а углы в градах или градусах, минутах и т. д.).

Веса разнородных измеренных величин, при совместном уравнивании их, вычисляются по обычным формулам, т. е. как величины, обратно пропорцио­нальные квадратам средних ошибок.

При этом безразлично, в каких единицах выражать средние ошибки измеренных величин, например, средние ошибки всех измеренных длин с одинаковым правом можно выражать или в метрах, или в сантиметрах, или в миллиметрах и т. д., а средние ошибки всех измеренных углов — или в секундах, или в минутах и т. д.

Необходимо только коэффициенты и свободные члены условных уравне- ' ний (при уравнивании методом условных уравнений) или уравнений ошибок (при уравнивании методом косвенных наблюдений) выражать в той же си­стеме единиц. При этом вероятнейшие поправки v к измеренным величинам также будут получаться в выбранных единицах. Конечно, постоянное про­извольное число А должно быть принято одним и тем же при вычислении весов всех измеренных величин как углов, так и длин и т. д.

Средняя ошибка единицы веса т₀, вычисляемая в результате уравнива­ния по обычной формуле

m_{0 =}

является величиной не именованной, так же как и при уравнивании одно­родных измерений.

Средняя ошибка измерения с весом р,. получаемая по результатам уравнивания, вычисляется также по обычной формуле

mi _{= =}

и имеет наименование, соответствующее наименованию, принятому при вы­числении веса.

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: