 |
Дисперсионный анализ (зависимые и независимые переменные)
|
|
|
|
С SPSS
УЧЕБНОЕ ПОСОБИЕ
(Электронный вид: http://socioline.ru)
Допущено Советом Учебно-методического объединения вузов России по образованию в области менеджмента в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности «Маркетинг»
Москва ИНФРА-М 2009
Рецензент:
Азоев Г.Л., д.э.н., профессор, директор Института маркетинга ГУУ
Моосмюллер Г., Ребик Н.Н. Маркетинговые исследования М74 с SPSS: Учеб. пособие. - М.: ИНФРА-М, 2009. - 160 с. - (Высшее образование).
ISBN 978-5-16-002811-8
В пособии подробно описаны основные методы статистического анализа, применяемые при обработке маркетинговой информации с использованием программного комплекса SPSS. Приводятся детальные инструкции пользования программой, показано, как проводить поэтапную интерпретацию результатов анализа.
| УДК 339.138(075.8) ББК 65.290-2я73 М74 |
Для студентов, обучающихся по специальности «Маркетинг» по дисциплинам «Маркетинговые исследования» и «Технологии маркетинговых исследований», для студентов-магистров и слушателей программы МВА. Может быть рекомендовано для студентов, обучающихся по специальностям «Статистика» и «Социология».
ISBN 978-5-16-002811-8
© Моосмюллер Г., Ребик Н.Н., 2007
ВВЕДЕНИЕ
Данная работа посвящена основным методам статистического анализа, применяемым при обработке маркетинговой информации с использованием программного комплекса SPSS (версия 13.0) для Windows.
SPSS (Statistical Package for Social Sciences или в новой интерпретации — Superior Performing Software Systems) — система (программный пакет) статистической обработки информации, которая предоставляет пользователю широкие возможности преобразования и анализа данных, а также наглядного представления полученных результатов.
|
|
|
Подробное описание структуры редактора данных, детальные инструкции по использованию SPSS, поэтапная интерпретация результатов анализа, содержащиеся в этой книге, предназначены для начинающих пользователей программы.
Наше пособие существенно отличается от многих учебных пособий по SPSS тем, что в нем инструкции для пользователей объединены с подробным описанием механизма действия применяемых методов анализа.
Особенность представления основных методов статистического анализа в данной работе заключается в отсутствии формул расчета статистических показателей. Механизм действия различных методов анализа описан с помощью рисунков и графиков.
Применение каждого из представленных в книге методов анализа иллюстрируется примерами из практики Института исследования рынка CenTouris (производная от словосочетания «центр туризма»), который специализируется на исследованиях туристического рынка Восточной Баварии.
Данное учебное пособие подготовлено по материалам лекций, которые читаются в Университете г. Пассау, и по программе МВА специальности «Маркетинг» в Государственном университете управления (Москва).
1. ОСНОВЫ СТАТИСТИЧЕСКОГО АНАЛИЗА В МАРКЕТИНГОВЫХ ИССЛЕДОВАНИЯХ
1.1. ФОРМИРОВАНИЕ СТАТИСТИЧЕСКОЙ ВЫБОРКИ
В ходе масштабных маркетинговых исследований сбор информации по каждому респонденту, представляющему интерес для исследователей, сопряжен со значительными затратами времени и средств и поэтому является нереальным или экономически нецелесообразным.
Например, если объектом исследования являются способы проведения досуга студентами города Москвы, то собрать информацию о каждом студенте проблематично. В этом случае из общей (генеральной) совокупности (из числа лиц, интересующих исследователей) производится статистическая выборка с целью определения круга лиц для участия в проведении исследований.
|
|
|
Основным требованием, предъявляемым к статистической выборке, является ее репрезентативность. Статистическая выборка считается репрезентативной (представительной), если она представляет собой «уменьшенную копию» генеральной совокупности и, следовательно, по данным, собранным в рамках статистической выборки, можно судить о генеральной совокупности в целом.
Существуют различные виды статистической выборки, которые отличаются по способу ее формирования, т.е. по технике проведения отбора. Различают случайную и эмпирическую выборки (табл. 1.1).
Случайная выборка характеризуется тем, что каждый элемент генеральной совокупности имеет шанс (отличный от нуля) оказаться в статистической выборке. При этом возможно рассчитать вероятность, с которой каждый элемент генеральной совокупности может оказаться в выборке.
Таблица 1.1
|
Существует несколько видов случайной выборки в зависимости от метода ее формирования (Schmalen, 2002. S. 390):
1. Простая случайная выборка предполагает, что все элементы генеральной совокупности имею! равные шансы оказаться в статистической выборке. Выбор производится по принципу лотереи. Элементы выборки извлекаются непосредственно из генеральной совокупности. Достоинство данного метода формирования выборки состоит в том, что не требуется знания структуры генеральной совокупности.
2. Взвешенная случайная выборка используется в том случае, если существует необходимость учитывать разделение генеральной совокупности на группы (слои). При этом известна структура генеральной совокупности (доли отдельных групп).
|
|
|
Статистическая выборка проводится случайным образом отдельно в каждой группе генеральной совокупности с сохранением пропорций соотношения размеров этих групп.
Например, в числе студентов, представляющих собой генеральную совокупность, 47% составляют юноши и 53% — девушки. При формировании взвешенной случайной выборки размером в 100 человек должны быть отобраны 47 юношей и 53 девушки (рис. 1.1). В результате этого, хотя отбор респондентов производится случайно, статистическая выборка имеет структуру, идентичную структуре генеральной совокупности, что повышает степень ее репрезентативности.

Рис. 1.1. Взвешенная случайная выборка
В качестве недостатков этого метода формирования статистической выборки следует отметить необходимость знания структуры генеральной совокупности и сложность организации сбора информации на практике.
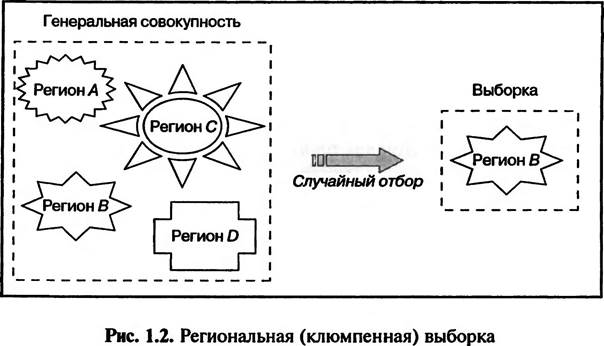
3. Клюмпенная выборка используется также в том случае, если генеральная совокупность разделена на группы (клюмпены). Из общего числа клюмпенов случайным образом выбирается один, который используется как статистическая выборка. Все элементы клюмпена становятся элементами статистической выборки.
Этот метод формирования выборки часто называется «региональным»: генеральная совокупность — страна (город), выборка — республика (район города) (рис. 1.2). Например, если в качестве генеральной совокупности выступают все студенты города Москвы, то для формирования клюмпенной выборки случайным образом может быть выбран один из столичных вузов.
Достоинство клюмпенной выборки состоит в более простой организации процесса сбора информации и снижении затрат (экономия на транспортных расходах).
Основным недостатком данного метода формирования статистической выборки является клюмпенный эффект, который состоит в том, что клюмпены могут существенно отличаться друг от друга по структуре, что обусловливает низкую степень репрезентативности клюмпенной выборки. Едва ли по данным, собранным при участии студентов только одного московского вуза, можно судить обо всех студентах города Москвы.
|
|
|
|
При формировании круга респондентов для проведения маркетинговых исследований использование случайной выборки не всегда возможно или целесообразно. Например, при сборе информации посредством наблюдения не всегда возможно заранее четко определить круг людей, которые окажутся в поле зрения наблюдателя.
Формирование случайной статистической выборки предполагает возможность сбора информации по каждому элементу генеральной совокупности. Однако такая возможность не всегда существует на практике. Например, проведение исследований на территории вуза требует получения согласия его администрации. Одно это обстоятельство может стать серьезным препятствием быстрому и оперативному сбору информации.
На практике часто применяют эмпирическую выборку, когда в круг респондентов для сбора информации включается каждый «первый встречный», согласный принять участие в исследовании (при проведении наблюдения такое согласие не всегда является необходимым условием). В этом случае возможно также использование квотированной выборки, когда структура неэмпирической выборки определена заранее (например, 50% женщин и 50% мужчин).
Эмпирическая выборка характеризуется низкой степенью репрезентативности. Результаты исследований при использовании эмпирической выборки зависят от места и времени сбора информации. Например, при изучении досуга студентов города
Москвы результаты исследования будуг определяться тем, где происходит сбор информации — у входа в ночной клуб или в библиотеку.
Статистическая выборка не используется при проведении качественных маркетинговых исследований, например исследований в форме экспертных опросов или фокус-групп. В этих случаях круг респондентов для проведения маркетинговых исследований формируется при помощи целенаправленной выборки.
При осуществлении целенаправленной выборки для участия в исследовании отбираются респонденты, которые могут предоставить наиболее точную и полную информацию (формирование экспертной группы), при участии которых можно организовать наиболее плодотворную дискуссию (формирование фокус- группы). В данном случае из числа потенциально возможных респондентов выбираются те, которые обладают наиболее ценной информацией и готовы поделиться ею для проведения исследований.
При формировании статистической выборки следует решить следующие вопросы:
1. Определит ь генеральную совокупность.
2. Определить размер выборки.
3. Выбрать метод формирования выборки.
|
|
|
Определение генеральной совокупности позволяет ответить на
вопрос: «Из каких потенциальных респондентов следует производить выборку?» Это не всегда является очевидным. Например, кого следует привлекать для сбора информации при изучении вопросов семейного отдыха: жен, мужей, других членов семьи, работников туристических фирм или, может быть, всех вместе? Чтобы ответить на этот вопрос, исследователям необходимо решить, какого типа информация им нужна и кто ею, скорее всего, обладает (Янкевич, Безрукова, 2002. С.111).
Размер выборки определяется экономической целесообразностью сбора информации. Увеличение размера выборки способствует повышению репрезентативности и, следовательно, точности результатов исследования, однако это сопряжено с дополнительными затратами. В этом случае необходимо взвешивать экономическую ценность получаемой информации и затраты, связанные с ее сбором.
Сбор первичной информации в рамках статистической выборки осуществляется в форме проведения опроса, наблюдения или эксперимента.
1.2. ОСНОВНЫЕ МЕТОДЫ СТАТИСТИЧЕСКОГО АНАЛИЗА
1.2.1. КЛАСТЕРНЫЙ АНАЛИЗ
Кластерный анализ — метод классификации объектов по заданным признакам. Задача кластерного анализа состоит в формировании групп:
• однородных внутри (условие внутренней гомогенности);
• четко отличных друг от друга (условие внешней гетерогенности).
Целью кластерного анализа в маркетинге является определение целевых групп потребителей, для которых было бы целесообразно разработать специальное торговое предложение, т.е. уникальную комбинацию инструментов маркетинга.
Пример. Курильщики сигар, возраст и уровень доходов которых известны, исследуются на предмет возможности их разделения на однородные группы (кластеры) (рис. 1.3).
В варианте В однородные кластеры не выявлены. Следовательно, целенаправленная дифференциация торгового предложения невозможна.
В варианте А выявлены две однородные группы курильщиков сигар: «старые и бедные», «молодые и богатые», которых можно считать двумя целевыми группами потребителей. В этом случае целесообразно разработать два специальных торговых предложения — уникальных по цене, уровню качества продукции, упаковке, системе продвижения товара и т.д. (Schmalen, 2003. S.401).

|
Элементы, включаемые в один и тот же кластер, имеют разную степень схожести (уровень отличия друг от друга). Техника кластерного анализа заключается в выявлении уровня схожести всех исследуемых элементов и последовательном объединении элементов в порядке возрастания уровня различия между ними. Число выявленных кластеров зависит от заданного уровня схожести (различия) элементов, включаемых в один кластер.
Техника кластерного анализа может быть проиллюстрирована дендограммоi, составляемой при помощи статистической компьютерной программы, втом числе SPSS (рис. 1.4).
На рис. 1.4 изображен результат кластерного анализа 18 предприятий розничной торговли, которые предлагают в качестве «особого предложения» (товары со скидками) один и тот же набор продуктов (примерно 50 наименований): молочные продукты, чистящие средства, косметика и т.д.
Целью кластерного анализа в данном случае является ответ на вопрос: возможно ли разделение исследуемых предприятий розничной торговли на кластеры в зависимости от их ценовой политики в плане формирования «особых предложений»
В результате проведения кластерного анализа было выявлено три кластера: А, В и С (рис. 1.4). Предприятия розничной торговли 6, 18, 16, 1,5, 15 (кластер А), так же как и 12, 2, 9, 17, 10 (кластер С), проводят одинаковую ценовую политику при формировании «особых предложений» (это, в частности, магазины торговых сетей EDEKA и REWE).

|
Предприятия розничной торговли, вошедшие в кластер В («Прочие»), не имеют одинаковой ценовой политики, но, тем не менее, их «особые предложения» имеют схожую ценовую структуру. Их можно объединить в одну группу только при задании определенного допустимого уровня их отличия друг от друга (Schmalen, 19. S. 402).
При повышении допустимого уровня отличия исследуемых элементов (снижении требований к однородности кластера) возможно объединение кластеров В и С, а затем присоединения к ним кластера А.
1.2.2. ДИСКРИМИНАНТНЫИ АНАЛИЗ
Дискриминантный анализ проводится с целью выявления различий между исследуемыми группами. Например, могут быть исследованы группы потребителей конкурирующих товаров (или покупатели конкурирующих брендов) на предмет того, существуют ли различия между исследуемыми группами по заданным признакам. Иными словами, цель анализа — выяснить, можно ли составить «типичный портрет покупателя» для каждой исследуемой группы по заданным характеристикам.
Пример. Владельцев BMW и VW возраст и доходы которых известны, исследуют на предмет того, можно ли разделить их (дискриминация) на две группы — «типичных владельцев BMW» и «типичных владельцев VW», так, чтобы группы владельцев характеризовались определенным уровнем дохода и возрастом (рис. 1.5).

|
На рис. 1.5 в системе координат заданных характеристик отмечены сочетания возраста и дохода каждого исследуемого владельца автомобилей (BMW и VW).
В ходе дискриминантного анализа предпринимается попытка разделить существующие группы автовладельцев по возрасту и уровню дохода при помощи дискриминантной линий. Дискрими- нантная линия должна быть проведена таким образом, чтоб комбинации характеристик владельцев автомобилей разных марок оказались расположенными по разные стороны линии и возможных пересечений было бы как можно меньше. В этом случае можно составить портрет «типичного владельца автомобиля определенной марки» по заданным характеристикам.
В варианте В возможны различные положения дискриминантной линии, при которых число пересечений будет в равной степени многочисленным. В данном случае невозможно разделить владельцев BMW и VW по уровню дохода и возрасту, т.е. не существует «портрета типичного владельца» BMW или VW.
В варианте А большая часть комбинаций уровней дохода и возраста владельцев VW лежит слева от дискриминантной линии, а владельцев BMW — справа. Это говорит о том, что владельцы BMW характеризуются более высоким уровнем дохода и относительно молоды по сравнению с владельцами VW (Schmalen, 2002. S. 403).
Характеристики «типичного потребителя», выявленные в результате проведения дискриминантного анализа, используются при прогнозировании поведения покупателей. Руководствуясь выявленными характеристиками «типичного покупателя», можно спрогнозировать, в пользу какого именно товара будет принято решение о покупке. В нашем примере (см. рис. 1.5) молодого человека с высоким уровнем дохода, желающего приобрести автомобиль, можно рассматривать как потенциального владельца BMW.
Если кластерный анализ выявляет возможность разбиения совокупности респондентов на группы, то дискриминантный анализ выявляет возможность установления различий уже существующих групп респондентов.
В настоящее время на практике для прогнозирования поведения потребителей используется более совершенный статистический метод — логистической регрессии. Этот метод позволяет не только ответить на вопрос, какой именно товар потребитель выберет скорее всего, но и определить вероятность, с которой потребитель выберет тот или иной товар.
висимая переменная Y). В варианте В существует много возможностей проведения регрессионной линии, когда сумма квадратов расстояний от точек эмпирических значений до регрессионной линии будет примерно одинаковой. Возникает так называемый эффект пропеллера. В этом случае линейная зависимость между исследуемыми переменными отсутствует.
В варианте А можно найти наилучший вариант положения регрессионной линии при помощи метода наименьших квадратов. В этом случае действительно существует прямая линейная зависимость между уровнем доходов населения и объемом розничной торговли (Schmalen, 2002. S. 405).
Результаты регрессионного анализа используются для составления прогнозов изменения количественных переменных путем перенесения выявленных тенденций на будущие периоды.
В рассматриваемом примере (см. рис. 1.6 — вариант Л) между уровнем дохода населения (X) и объемом торгового оборота (У) существует линейная зависимость У = с + b - X. Если существует достаточно надежный прогноз относительно роста доходов населения (X), тогда исходя из данных прогноза (Л") и регрессионной зависимости (У = а + b • X) можно составить прогноз роста объемов оборота розничной торговли (У).
Использование регрессионного анализа в прогнозировании сопряжено с рядом проблем.
Во-первых, исходя из наличия достаточно устойчивой статистической зависимости не всегда можно делать выводы о существовании каузальной (причинно-следственной) взаимосвязи. В нашем примере результаты регрессионного анализа не доказывают того, что растущий уровень доходов населения является причиной роста объемов оборота розничной торговли.
Во-вторых, результаты регрессионного анализа могут быть использованы для построения прогнозов только в случае верности «гипотезы стабильности во времени», т.е. если не происходит никаких структурных изменений. Гипотеза стабильности во времени предполагает изменение во времени только исследуемых переменных, все прочие величины являются постоянными. В приведенном выше примере рассматривается влияние уровня дохода на оборот розничной торговли. Предполагается, что степень влияния прочих факторов (например, цены, склонности потребителей к накоплению и т.д.) остается неизменной.
На практике результаты регрессионного анализа используются для составления прогнозов, как правило, в сочетании с опросами
1.2.3. РЕГРЕССИОННЫЙ АНАЛИЗ
Регрессионный анализ — метод выявления статистической зависимости между исследуемыми переменными. На основе анализа эмпирических данных (данных, собранных в ходе проведения исследования) описывается не только сам факт существования статистической зависимости, но также описывается и математическая формула функции зависимости исследуемых переменных.
Современная техника регрессионного анализа позволяет описывать функции зависимости исследуемых переменных различных видов. Самая простая — линейная функция, определяемая при помощи линейного регрессионного анализа.
Стандартная модель простой линейной регрессии имеет вид
Y=a+b*X
где X — независимая переменная (фактор, влияющий на объект исследования);
Y — зависимая переменная (объект исследования);
a, b — постоянные величины (параметры модели).
Определение параметров модели (а, b) осуществляется путем применения метода наименьших квадратов. Регрессионная линия должна быть проведена в «облаке эмпирических значений» таким образом, чтобы сумма квадратов вертикальных и горизонтальных расстояний от каждой точки до регрессионной линии была бы минимальной (рис. 1.6).
На рис. 1.6 показана технология выявления зависимости между исследуемыми переменными: уровнем дохода населения (независимая переменная X) и объемом оборота розничной торговли (за-

|
экспертов. Такая комбинация количественных и качественных методов маркетинговых исследований соединяет точность математических расчетов со знаниями и интуицией экспертов.
1.2.4. ФАКТОРНЫЙ АНАЛИЗ
Факторный анализ — метод, который позволяет сгруппировать большое число переменных (факторов, влияющих на предмет исследования) и свести их к минимальному числу «обобщающих факторов». Группировка данных производится по принципу:
· переменные, имеющие между собой высокую степень корреляции (тесную взаимосвязь), объединяются в один фактор;
· переменные, отнесенные к разным «обобщающим факторам», имеют между собой низкую степень корреляции (слабую взаимосвязь).
Факторный анализ производится в том случае, если существует огромный массив данных, который необходимо уменьшить («сжать») для проведения дальнейших исследований.
Например, существует база данных по результатам опроса, в ходе которого туристы, отдыхающие в курортной зоне «Баварский лес», оценивали эту курортную зону. Респонденты оценивали степень важности для них каждого из 13 предложенных мотивов выбора места отдыха (табл. 1.2).
Предположим, исследователям необходимо провести кластерный анализ туристов, отдыхающих в курортной зоне «Баварский лес», по таким характеристикам, как гражданство, уровень дохода и мотив выбора места отдыха. Проведение кластерного анализа затруднительно из-за больших размеров массива данных, содержащего информацию о мотивах проведения отпуска в «Баварском лесу», и из-за ограничений мощности вычислительной техники. Для удобства проведения кластерного анализа необходимо уменьшить объем («сжатие») данных при помощи факторного анализа.
В ходе факторного анализа осуществляется попарное сравнение исследуемых переменных с целью определения их схожести друг с другом, а также определяется число «группирующих факторов». В табл. 1.2 представлены результаты факторного анализа в рассматриваемом примере. Заданные 13 мотивов выбора места отдыха объединены в 4 фактора, определяющих выбор туристов в пользу «Баварского леса»:
1) гостеприимство по приемлемым ценам;
2) общение с природой;
3) специальное предложение Восточной Баварии;
4) культурная программа.
Также в табл. 1.2 представлены коэффициенты корреляции, которые характеризуют степень взаимосвязи между группируемыми переменными и группирующими факторами. Значения коэффициентов корреляции изменяется от-1 до +1.
Значение коэффициента корреляции, близкое к нулю, указывает на низкую степень взаимосвязи. Например, национальный колорит и самобытность «Баварского леса» (фактор «Специальное предложение Восточной Баварии») не обусловливается приемлемым уровнем цен (коэффициент корреляции 0,00055).
Отрицательное значение коэффициента корреляции указывает на существование обратной взаимосвязи. Например, приемлемые цены слабо отрицательно влияют на привлекательность «Баварского леса» с точки зрения общения с природой (коэффициент корреляции 0,01297). Это объясняется тем, что приемлемые цены привлекают множество туристов, что не способствует созданию атмосферы общения с природой.
Значение коэффициента корреляции, близкое к -1, указывает на наличие сильной обратной взаимосвязи. Такие случаи в рассматриваемом примере отсутствуют.
Таблица 1,2
Результаты факторного анализа, проводимого при оценке
курортной зоны «Баварский лес»
(адаптировано по: Schmalen, 2002. S. 404)
|
Если значение коэффициента корреляции близко к +1, это свидетельствует о существовании плотной прямой взаимосвязи. Например, возможность заниматься пешим туризмом в лесу во многом определяет привлекательность рассматриваемого региона для тех, кто ценит общение с природой (коэффициент корреляции 0,81047) (см. табл. 1.2).
Характеристики объекта исследования объединяются в один обобщающий фактор при наличии высокой степени корреляции — как позитивной, так и негативной (в рассматриваемом примере встречается только сильная позитивная корреляция). Например, приемлемые цены, вкусная еда, гостеприимство и комфорт отдыха с детьми обобщаются в один фактор привлекательности курорта — «Гостеприимство по приемлемым ценам».
При допуске определенной потери информации (в данном случае 30%) впоследствии анализируются не 13 факторов, а только четыре. Такое «сжатие» данных существенно упрощает дальнейшее проведение исследования без существенной потери информации.
Факторный анализ целесообразно проводить только в том случае, если он предшествует применению других методов статистического анализа.
На практике факторный анализ всегда применяется в комбинации с другими статистическими методами обработки информации. Его можно охарактеризовать как вспомогательный метод, позволяющий упростить исследования путем сокращения анализируемой информации.
1.2.5. ДИСПЕРСИОННЫЙ АНАЛИЗ
Дисперсионный анализ — метод, при помощи которого исследуется влияние одной или нескольких независимых переменных на одну или несколько зависимых переменных.
Например, один и тот же продукт продается в нескольких регионах в упаковке разных типов (табл. 1.3). На основе данных объема продаж, сгруппированных по указанным признакам, нужно определить, имеют ли существенное влияние на результаты продаж:
• регион и тип упаковки (основной эффект);
• комбинация этих факторов (интерактивный эффект).
Дисперсионный анализ (зависимые и независимые переменные)
| Независимая переменная № 1 (категориапьный фактор) | Независимая переменная № 2 (категориальный фактор) | ||
| Регион 1 | Регион II | Регион III | |
| Показатели объема продаж (тыс. шт.) (зависимая переменная) | |||
| Тип упаковки А | |||
| Тип упаковки В | |||
| Тип упаковки С |
Возможно, что исследуемые факторы влияют на объект исследования только в сочетании друг с другом. Например, упаковка, предназначенная для помещения в микроволновую печь, может способствовать значительному увеличению объемов продаж только в крупных городах.
Различают несколько видов дисперсионного анализа — в зависимости от числа исследуемых переменных (табл. 1.4).
Пример постановки вопроса однофакторного дисперсионного анализа: влияет ли тип рекламы (плакаты, объявления в сред-
|
|
|


