 |
Линейный регрессионный анализ в SPSS
|
|
|
|
Регрессионный анализ служит для выявления влияния одной или нескольких независимых переменных на одну зависимую переменную. С точки зрения чистоты статистических расчетов в регрессионном анализе могут участвовать лишь метрические, т.е. количественные, переменные (см. подраздел 2.3 «Типы шкал измерения переменных»). Однако в некоторых учебниках по SPSS указывается, что в регрессионном анализе могут участвовать как метрические, так и порядковые переменные.
Дихотомические переменные (имеющие только два значения: высокий/низкий, близкий/далекий и т.п.) могут рассматриваться как метрические. В случае необходимости использовать в регрессионном анализе номинальные переменные их следует разложить на дихотомические переменные (см. подраздел 2.2 «Виды кодировки данных»).
Регрессионный анализ позволяет не только сделать вывод о существовании взаимосвязи между исследуемыми переменными, но и дать математическое описание зависимости межд5 ними.
Современные методы статистического анализа позволяют давать математическое описание зависимости переменных, выраженных в функциях различных видов. Техника регрессионного анализа, позволяющая выявлять и описывать взаимосвязи в виде линейных функций, называется линейным регрессионным анализом (см. подраздел 1.2 «Основные виды статистического анализа»).
Для выявления и описания линейной зависимости между объектом исследования (зависимой переменной) и одним фактором, возможно влияющим на него (независимой переменной), используется простая линей чая регрессия. Регрессионная модель (регрессионное уравнение) в этом случае имеет вид
у = а — Ьх,
где у — зависимая переменная;
х — независимая переменная;
а — свободный член (константа);
b — коэффициент регрессии.
|
|
|
Для выявления и описания линейной зависимости между объектом исследования (зависимой переменной) и несколькими факторами, возможно на него влияющими (независимыми переменными), используется множественная линейная регрессия. Регрессионная модель (регрессионное уравнение) в этом случае имеет вид
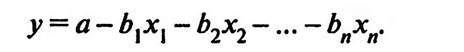
Результатом регрессионного анализа является регрессионная модель (регрессионное уравнение), а именно — определение свободного члена (а) и коэффициентов регрессии (b).
Также в ходе регрессионного анализа определяются стандартизированные коэффициенты регрессии (Beta). Данные коэффициенты позволяют судить о значении соответствующих независимых переменных (х), т.е. о степени влияния на зависимую переменную (у).
Результатом регрессионного анализа является не только регрессионная модель, но также расчет ряда показателей, характеризующих статистическую значимость и практическую применимость построенной модели. Среди таких показателей в качестве основных можно выделить:
* Коэффициент детерминации (R) — является характеристикой общей силы линейной связи между переменными в регрессионной модели. Значения коэффициента находятся в интервале от нуля до единицы. Чем ближе значение коэффициента к единице, тем плотнее линейная взаимосвязь, описанная в регрессионной модели. В общем случае он должен превышать 0,5.
* Коэффициент R-квадрат (R Square) — показывает, какая доля совокупной вариации в зависимой переменной описывается независимой переменной. Значения коэффициента лежат в интервале от нуля до единицы. Как правило, данный показатель должен превышать 0,5. Если он равен 0,5, это говорит о том, чго регрессионная модель описывает 50% случаев, т.е. она справедлива только для 50% исходных данных. Важной частью регрессионного анализа является анализ остатков, т.е. отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (не систематически) и подчиняться случайному распределению. Проверка наличия систематических связей между остатками может быть произведена при помощи теста Дарбина—Уотсона (Durbin— Watson) на автокорреляцию. Этот тест позволяет рассчитать коэффициент, значение которого варьирует от 0 до 4. Если значение данного коэффициента близко к 2, это означает, что автокорреляция отсутствует.
|
|
|
Линейный регрессионный анализ проводится в SPSS с помощью меню «Analyze > Regression > Linear...» (рис. 4.1).
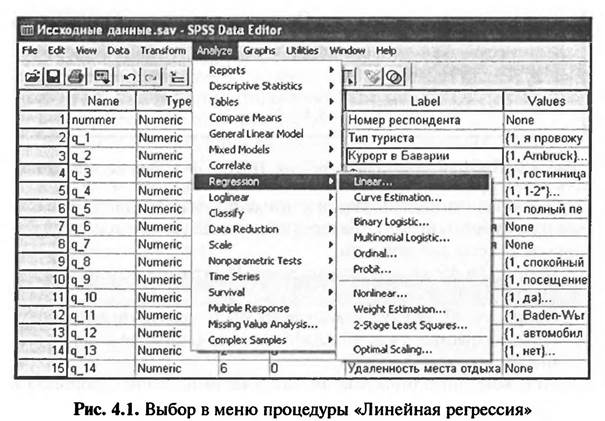
После выбора меню, представленного на рис. 4.1, открывается диалоговое окно «Линейная регрессия», при помощи которого формируется задание на проведение анализа в SPSS. Набор команд данного задания обусловливается тем, какой именно вид линейной регрессии используется — простая или множественная линейная регрессия.
4.1. ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
4.1.1. ПОСТАНОВКА ЦЕЛИ ИССЛЕДОВАНИЯ И ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ В SPSS
Как отмечалось ранее, простая линейная регрессия используется дчя выявления и описания линейной зависимости между двумя исследуемыми переменными — зависимой и независимой.
Например, следует определить, в какой зависимости находятся такие переменные, как сумма общих расходов туристов на проведение отпуска и сумма, уплачиваемая туристами за проживание в отеле или пансионе (включая обслуживание) (рис. 4.2).

Для анализа используются данные опроса туристов, отдыхающих в курортной зоне «Баварский лес». Для анализа из всех вопросов анкеты выбраны два:
• Вопрос № 45: «Какую сумму денег Вы тратите в целом на отдых?»
• Вопрос № 47: «Какую сумму денег Вы тратите во время отдыха на проживание в гостинице/пансионе (включая обслуживание)?»
При занесении информации по ответам на данные вопросы в файл данных SPSS была использована двойная запись переменных (см. подраздел 2.2 «Виды кодировки данных»). Каждый из этих вопросов представлен в файле данных SPSS в виде двух переменных (рис. 4.3).

Вопрос № 45 представлен в виде двух переменных с именами «q_45_1» и «q_45_2» и одинаковыми метками «Общие расходы на отдых». Вопрос № 47 представлен в виде двух переменных с именами «q_47_1» и «q_47_2» и одинаковыми метками «Расходы на проживание».
|
|
|
Переменные с именами «q_45_l» и «q_47_l» являются номинальными. Значення меток этих переменных имеют числовые коды («1» — «сумма в евро», «98» — «не знаю», «99» — «нет данных»). Они указывают на то, назвал ли респондент точную сумму в качестве ответа на поставленный вопрос или нет.
Переменные с именами «q_45_2» и «q_47_2» являются метрическими. В столбце «Values» таблицы «Свойства переменных» отсутствуют значения меток переменных (см. рис 4.3). Значения этих переменных выражаются в конкретных денежных суммах и отображаются в столбцах «q_45__ I» и «q_47_2» таблицы «Значения переменных» (рис. 4.4).

Фрагмент таблицы «Значения переменных» файла данных SPSS, представленный на рис. 4.4, содержит информацию о расходах респондентов во время отдыха. Респондент в строке 2194 потратил на отдых в целом 2200 евро, на оплату гостиницы/ пансиона — 800 евро. Респондент в строке 2197 потратил на отдых в целом 1400 евро, а на оплату гостиницы/пансиона — 300 евро и т.д.
Преимуществом простой линейной регрессии является возможность представить результаты анализа графически. Регрессионное уравнение, представляющее собой линейную функцию с одной переменной, может быть представлено в виде линейного графика в двухмерной системе координат.
Линейный регрессионный анализ применяется для графического прогнозирования поведения одной переменной в зависимости от изменения другой. Как правило, целью регрессионного анализа в данном случае является построение тренда, т.е. линейного графика, отображающего зависимость между переменными.
Исходя из полученного уравнения регрессии можно предсказать, каким будет значение одной переменной при изменении другой. В рассматриваемом примере регрессионная модель позволит спрогнозировать, как будут расти (уменьшаться) общие расходы на проведение отпуска при увеличении (уменьшении) расходов на проживание, включая обслуживание.
4.1.2. КОМАНДЫ SPSS НА ВЫПОЛНЕНИЕ ПРОСТОГО РЕГРЕССИОННОГО АНАЛИЗА
Запрос на выполнение линейного регрессионного анализа осуществляется в одноименном диалоговом окне (L near Regression) (рис. 4.5), которое открывается при выборе в меню «Analyze > > Regression > Linear...»(см. также рис. 4.1).
|
|
|
В левом поле диалогового окна «Линейная регрессия» (Linear Regression) представлен список меток всех переменных, занесенных в базу данных. Из этого списка выбирается зависимая переменная и переносится в поле «Dependent». В рассматриваемом примере это переменная, имеюшая метку «Общие расходы на отдых». В базе данных такую мегку имеют две переменные. В данном случае выбирается переменная, значения которой представляют собой денежные суммы в евро.
Из списка всех существующих в базе данных меток переменных также выбирается независимая переменная и переносится в поле «Independent^)». В рассматриваемом примере это переменная, имеющая метку «Расходы на проживание». В базе данных такую метку имеют две переменные. В данном случае выбирается переменная, значения которой представляют собой денежные суммы в евро.
В диалоговом окне «Линейная регрессия» в поле «Метод» (Method) следует указать метод Еключения переменных в регрессионную модель. По умолчанию задается метод «Enter». В случае осуществления простого регрессионного анализа рекомендуется использовать именно этот метод.

Если бы нужно было построить регрессионные модели для отдельных групп респондентов, то в поле «Selection Var able» диалогового окна «Линейная регрессии» нужно было бы указать переменную, по которой производится отбор респондентов в исследуемые группы. Например, если бы нужно было построить две регрессионные модели для мужчин и для женщин, то из общего списка переменных в поле «Seiect on Varable» следовало бы переместить метку переменной «Пол».
В главном диалоговом окне «Линейная регрессия» имеются четыре кнопки («Statistics», «Plots», «Save» и «Options»), при нажатии которых открываются вспомогательные диалоговые окна.
При нажатии кнопки «Statisti:s» на экране появляется одноименное диалоговое окно «Статистические показатели» (рис. 4.6). В нем задаются команды на расчет различных статистических показателей. В рассматриваемом примере поставлена отметка напротив команды «Est mates». В результате выполнения данной команды рассчитываются коэффициент детерминации (К), коэффициент R-квадрат (R Square) и некоторые другие статистические показатели, необходимые для оценки качества построенной регрессионной модели.
Также в диалоговом окне «Статистические показатели» можно задать вычисление показателей, используемых для анализа остатков (Residuals). В рассматриваемом примере задается команда на выполнение теста Дарбина—Уотсона1.
|
|
|

При нажатии кнопки «Сот пие» в диалоговом окне «Статистические показатели» данное окно закрывается и осуществляется возврат в главное диалоговое окно «Линейная регрессия». После
1 Тест Дарбина—Уэтсона (Durbin— Watson Test) — тест на автокорреляцию. Автокорреляция выражается в наличии систематических связей между остатками.
В соответствии с теорией статистики уравнение простой регрессии (регрессионная модель) имеет вид у = а + bх + е,
где e — остатки (отклонения наблюдаемых значений от теоретически ожидаемых).
Остатки должны появляться случайно, т.е. не систематически. Для проверки этого условия проводится тест Дарбина—Уотсона. В ходе проведения этого тес га рассчитывается коэффициент, значение которого лежит в диапазоне от 0 до 4. Если значение коэффициента близко к среднему (т.е. к 2), это означает, что автокорреляция отсутствует, т.е. остатки появляются случайным образом.
нажатия кнопки «ОК» в диалоговом окне «Линейная регрессия» запускается процедура выполнения простого регрессионного анализа.
4.1.3. ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ ПРОСТОГО РЕГРЕССИОННОГО АНАЛИЗА
В качестве результатов линейного регрессионного анализа SPSS выводит на экран компьютера три таблицы: «Model Summary», «ANOVA» и «Coefficients» (табл. 4.1,4.2 и 4.3).
Таблица 4.1 Model Summary13
|
| а Predictors - влияющие переменные (константа): расходы на проживание. b Dependent Variable - зависимая переменная: общие расходы на отдых. |
В табл. 4.1 представлены основные показатели, оценивающие качество линейной модели, построенной в результате проведения регрессионного анализа.
В рассматриваемом примере значение коэффициента детерминации R составляет 0,605 (>0,5), что свидетельствует о наличии тесной линейной взаимосвязи между суммой общих расходов на проведения отпуска и суммой, уплачиваемой туристами за проживание в гостинице или пансионе.
Коэффициент R-квадрат (R Square) в рассматриваемом примере составляет всего 0,366. Это означает, что построенная регрессионная модель описывает только 36,6% случаев, когда увеличение суммы оплаты за проживание в гостинице или пансионе влечет за собой увеличение общих расходов на проведение отпуска. Это необходимо учитывать при применении результатов анализа в прогнозировании расходов туристов.
Значение теста Дарбина—Уотсона на автокорреляцию в рассматриваемом примере составляет 1,874 (см. табл. 4.1), т.е. близко к 2. Это говорит об отсутствии систематических связей между остатками, т.е. между отклонениями наблюдаемых (эмпирических) значений от теоретически ожидаемых (расчетных).
Таблица 4.2 ANOVAb
|
| а Predictors - влияющие переменные (константа): расходы на проживание. b Dependent Variable - зависимая переменная: общие расходы на отдых. |
В последнем столбце таблицы «ANOVA» (см. табл. 4.2) значение показателя «Статистическая значимость» (Sig.) должно быть меньше или равно 0,5. В рассматриваемом примере этот показатель составляет ноль. Это свидетельствует о том, что регрессионная модель, построенная на основе данных респондентов, попавших в выборку, справедлива для всей генеральной совокупности в целом.
Результаты регрессионного анализа, описывающие построенную регрессионную модель, представлены в табл. 4.3.
Таблица 4.3 Coefficients8
|
| а Dependent Variable - зависимая переменная: общие расходы на отдых. |
В столбце «В» таблицы «Коэффициенты» представлены параметры построенной регрессионной модели. В рассматриваемом примере уравнение регрессии имеет вид у = 642,273 + 1,596х.
Величина «Constant» показывает значение зависимой переменной при нулевом значении независимой переменной. Построенная регрессионная модель в рассматриваемом примере показывает, что если турист не тратит никаких денег за проживание в отеле или пансионе (например, если он остановился у друзей или живет в палатке), то его общие расходы на проведение отпуска в среднем составят 642,273 евро.
В следующем столбце табл. 4.3 представлены стандартные ошибки (Std. Error). При доверительном интервале 95% каждый коэффициент может отклоняться от средней величины на ±2 х xStd.Error. Например, сумма общих расходов на проведение отпуска при нулевых затратах на проживание в гостинице или пансионе может отклоняться от среднего значения (642,273 евро) на ± 2 • 31,526, т.е. на ± 63,052 евро.
Значение коэффициента регрессии независимой переменной «Затраты на проживание в гостинице или пансноне» в построенной модели составпяет 1,596. Это означает, что увеличение затрат на проживание в отеле или пансионе на 1 евро влечет за собой увеличение суммы общих затрат на проведение отпуска на 1,596 евро.
4.1.4. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРОСТОЙ РЕГРЕССИОННОЙ МОДЕЛИ В SPSS
Как уже было отмечено выше, основным достоинством линейной регрессии является возможность наглядного представления результатов анализа в виде линейного графика в двухмерной системе координат. Задание на построение такого графика осуществляется в SPSS в опции «Graphs».
При выборе меню «Graphs > Scatter» на экране появляется диалоговое окно «Scatte/Dot» («Диаграмма рассеяния»), в котором следует выбрать тип диаграммы. В данном случае следует выбрать диаграмму «Si rnple Scatter» (рис. 4.7).

Путем нажатия кнопки «Define» в диалоговом окне «Scatte/Dot» («Диаграмма рассеяния») на экране компьютера появляется новое диалоговое окно «Simple Scatterplot» («Простая диаграмма рассеяния») (рис- 4.8).

В левом поле диалогового окна «Простая диаграмма рассеяния» указываются метки всех переменных, содержащихся в исходном файле данных SPSS. Из списка меток всех переменных следует выбрать метку зависимой переменной и перенести ее в правое поле окна «YAxis». В рассматриваемом примере это метка переменной «q_45_2» — «Общие расходы на отдых».
Далее из списка всех переменных, представленных в левом поле окна «Простая диаграмма рассеяния», следует выбрать метку независимой переменной и перенести ее в правое поле окна «XAxis». В рассматриваемом примере это метка переменной «q_47__2» — «Расходы на проживание».
Нажав кнопку «ОК» в диалоговом окне «Простая диаграмма рассеяния», мы закрываем данное окно, и на экране компьютера появляется диаграмма рассеяния. К данному рисунку следует подвести курсор мыши и нажать кнопку мыши два раза. В результате этой операции на экране появится диалоговое окно «Chart Editor» («Редактор диаграмм») (рис. 4.9).
В диалоговом окне «Chart Editor» следует выбрать меню «Elements > Fit Line at Total», в результате чего на экране появится новое диалоговое окно «Properties» («Свойства») (см. рис. 4.9).
Во вкладке «Fit Line» («Приближенная линия») диалогового окна «Properties» («Свойства») следует отметить линейный вид графика — «Linear» (рис. 4.10).
После нажатия кнопки «Close» в диалоговом окне «Свойства» (рис. 4.10) данное окно закрывается. На рисунке построенной ранее диаграммы рассеяния (см. рис. 4. 10 — без линии тренда) появляется линия, отображающая линейную регрессионную модель. Следует отвести курсор мыши от рисунка и нажать клавишу мыши, в результате чего закроется диалоговое окно «Chart Editor» («Редактор диаграмм») и на экране останется только построенный график (рис. 4.11).


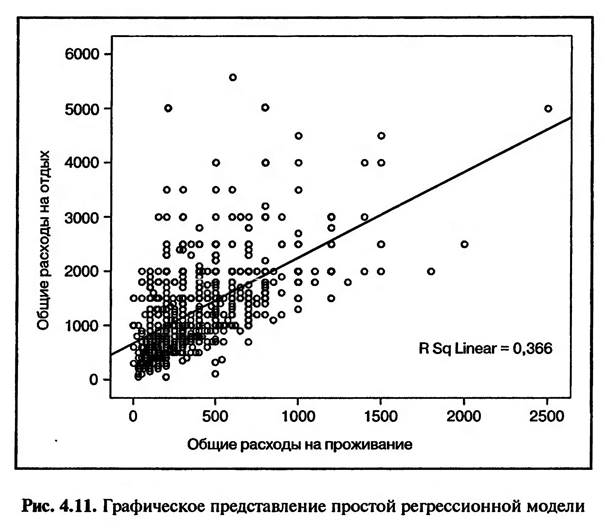
На рис. 4.11 представлено графическое изображение регрессионной модели у = 642,273 + 1,596х. Используя эту модель, можно прогнозировать, как будут изменяться общие расходы на отдых при изменении расходов на проживание в гостинице/пансионе для туристов, отдыхающих в курортной зоне «Баварский лес».
Построенная нами регрессионная модель описывает только 36,6% всех данных, полученных в результате опроса туристов. Это говорит о том, что вероятность ошибки при использовании данной регрессионной модели в целях прогнозирования достаточно велика.
4.2. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
4.2.1. ПОСТАНОВКА ЦЕЛИ ИССЛЕДОВАНИЯ И ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ В SPSS
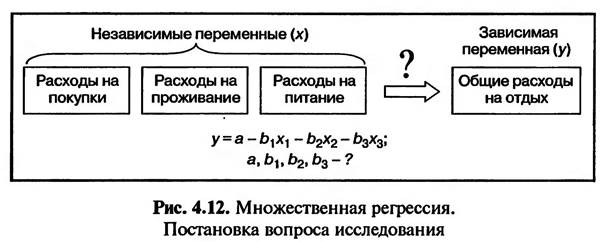
Как отмечалось ранее, множественная линейная регрессия используется для выявления и описания линейной зависимости между одной зависимой переменной и несколькими независимыми переменными. Например, следует определить, в какой зависимости между собой находятся общие расходы туристов на проведение отдыха и следующие статьи расходов:
• на покупки (одежды, обуви, галантерейных товаров, украшений, фотоаппаратов и т.д.);
• на проживание в отеле или пансионе (включая расходы на обслуживание);
• на питание (покупки продуктов в магазинах, посещение кафе и ресторанов).
Для проведения анализа используются данные опроса туристов, отдыхающих в курортной зоне «Баварский лес». Для проведения анализа из всех вопросов анкеты выбраны четыре:
• Вопрос № 45: «Какую сумму денег Вы тратите в целом на отдых?»
• Вопрос № 46: «Какую сумму денег Вы тратите во время отдыха на покупки (такие, как одежда, обувь, галантерея, украшения, фотоаппараты и т.д.)?»
• Вопрос № 47: «Какую сумму денег Вы тратите во время отдыха на проживание в гостинице/пансионе (включая расходы на обслуживание)?»
• Вопрос № 8: «Какую сумму денег Вы тратите во время отдыха на питание (т.е. на покупку продуктов в магазинах, посещение кафе и ресторанов)?»
При занесении информации по ответам на данные вопросы в файл данных SPSS была использована двойная запись переменных (см. подраздел 2.2 «Виды кодировки данных»). Каждый вопрос представлен в файле данных SPSS в виде двух переменных. Представление этих переменных в файле данных SPSS проиллюстрировано в подразделе 4.1 «Простая линейная регрессия» (см. рис. 4.3 и 4.4).
Множественная линейная регрессия отпичается от простой линейной регрессии рядом особенностей. Первая особенность состоит в невозможности графического изображения множественной регрессионной модели, что, конечно, наносит ущерб наглядности представления результатов анализа (см. рис. 4.12).
Другой особенностью множественной линейной регрессии является то, что переменные, объявленные независимыми, могут сами коррелировать между собой, т.е. возможно существование причинно-следственных связей между ними. В этом случае возникает эффект мультиколлинеарности.
Эффект мультиколлинеарности заключается в том, что независимые переменные, включенные в регрессионную модель, обозначают в принципе одно и то же. Например, в качестве зависимой переменной объявлена заработная плата выпускника университета, а в качестве независимых переменных — средний балл успеваемости во время учебы в университете и индекс интеллект Поскольку успеваемость студента во многом определяется уровнем интеллекта, в данной регрессионной модели возможно появление ложных корреляций.
Одним из условий построения множественной регрессионной модели является отсутствие или низкая степень корреляции между независимыми переменными. Для проверки соблюдения этого условия при проведении регрессионного анализа необходимо сначала производить диагностику наличия коллинеарности между независимыми переменными.
4.2.2. КОМАНДЫ SPSS НА ВЫПОЛНЕНИЕ МНОЖЕСТВЕННОГО
РЕГРЕССИОННОГО АНАЛИЗА
Запрос на выполнение линейного регрессионного анализа осуществляется в одноименном диалоговом окне (L near Regression) (рис. 4.13), которое открывается при выборе в меню «Analyze > Regression > Linear...»(см. рис. 4.1).
В левом поле диалогового окна «Линейная регрессия» (Linear Regression) представлен список меток всех переменных, занесенных в базу данных. Из этого списка выбирается зависимая переменная и переносится в поле «Dependent». В рассматриваемом примере это будет переменная, имеющая метку «Общие расходы на отдых», значения которой представляют собой денежные суммы в евро.
Из списка существующих в базе данных меток переменных также выбираются независимые переменные и переносятся в поле «Independents)». В рассматриваемом примере это переменные, имеющие метки: «Расходы на покупки», «Расходы ка проживание» и «Расходы на питание». Значения отобранных переменных — денежные суммы в евро.
Далее в диалоговом окне «Линейная регрессия» в поле «Метод» (Method) следует указать метод включения переменных в регрессионную модель. Из четырех методов, предлагаемых SPSS («Enter», «Stepwise», «Forward» и «Backward»), следует выбрать один. По умолчанию задается метод «Enter».
Метод «Enter» предполагает одновременную обработку всех независимых переменных, выбранных для анализа, он рекомендуется для случая простого регрессионного анализа с одной независимой переменной. Для множественного регрессионного анализа рекомендуется выбрать один из пошаговых методов, которые предполагают поэтапное включение независимых переменных в регрессионную модель. В нашем примере выбран метод «Stepwise».
При нажатии кнопки «Statistics» в главном диалоговом окне «Линейная регрессия» (см. рис. 4.13) на экране появляется одноименное диалоговое окно (рис. 4.14).
Диалоговое окно «Статистические показатели» уже было представлено в подразделе 4.1 «Простая линейная регрессия» на рис. 4.6. В данном окне задаются команды на расчет статистических показателей, характеризующих качество построенной регрессионной модели.

В рассматриваемом примере в диалоговом окне «Статистические показатели» отмечена команда «Estimates», при выполнении которой рассчитываются коэффициент детерминации (R), коэффициент R-квадрат (R Square). Так же отмечена команда «Durbiп—Watson», при выполнении которой производится тест Дарбина— Уотсона на автокорреляцию. Эти команды уже были подробно рассмотрены в подразделе 4.1 «Простая линейная регрессия».
Особенность множественного регрессионного анализа состоит в необходимости проверить наличие взаимосвязей между независимыми переменными. Для этого проводится диагностика коллинеарности, которая задается отметкой напротив команды «Collinearitу diagnostics» в диалоговом окне «Статистические показатели».
Нажав кнопку «Продолжение» (Contiпие) в диалоговом окне «Статистические показатели» (рис. 4.14) мы закрываем данное окно и возвращаемся в главное диалоговое окно «Линейная регрессия» (см. рис. 4.13). После нажатия кнопки «ОК» в главном диалоговом окне "Линейная регрессия» запускается процедура выполнения анализа.
4.2.3. ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ МНОЖЕСТВЕННОГО РЕГРЕССИОННОГО АНАЛИЗА
В качестве результатов линейного регрессионного анализа SPSS выводит на экран компьютера три таблицы: «Model Summary», «ANOVA» и «Coefficients» (табл. 4.4,4.5 и 4.6).
Поскольку при формировании задания на выполнение анализа был выбран пошаговый метод включения независимых переменных в регрессионную модель «Stepwise», то при представлении результатов анализа формируется несколько регрессионных моделей. В рассматриваемом примере таких моделей три (по числу независимых переменных). В соответствии с целями исследования основным результатом анализа является третья регрессионная модель, включающая все три независимые переменные (табл. 4.4).
Сводная таблица модели Model Summary4
| Model | R | R Square | AjustedR Square | Std. Error of the Es mate | Durbin-Watson |
| ,789е | ,623 | ,622 | 444,996 | ||
| ,889ь | ,790 | ,789 | 332,301 | ||
| ,937е | ,879 | ,878 | 252,373 | 1,930 |
8 Predictors - влияющие переменные (константа): расходы на покупки. b Predictors - влияющие переменные (константа): расходы на покупки,
расходы на проживание. с Predictors - влияющие переменные (константа): расходы на покупки,
расходы на проживание, расходы на питание. d Dependent Variable - зависимая переменная: общие расходы на отдых.
В сводной таблице модели представлены показатели, характеризующие качество построенных регрессионных моделей. В соответствии с целями исследования основным результатом нашего анааиза является третья регрессионная модель, включающая все три независимые переменные.
В нашем примере значение коэффициента детерминации (R) составляет 0,937 (возможные значения от нуля до единицы), что свидетельствует о наличии плотной линейной взаимосвязи между суммой общих расходов на отпуск и суммами, расходуемыми туристами на текущие покупки, проживание и питание.
Коэффициент R-квадрат (R Square) составляет 0,879. Это означает, что наша регрессионная модель описывает 87,9% случаев, т.е. ответов респондентов о структуре их расходов на отпуск.
Показатели коэффициента детерминации и коэффициента R-квадрат для первых двух моделей ниже, чем для третьей модели
(см. табл. 4.4). Также значения стандартной ошибки расчетов для первых двух моделей выше, чем для третьей. Это доказывает целесообразность включения в регрессионную модель всех ipex независимых переменных.
Сводная таблица модели представляет также результат теста Дарбина—Уотсона на автокорреляцию, значение которого должно быть приближено к 2, что свидетельствует об отсутствии системных связей между остатками, т.е. между отклонениями эмпирических (наблюдаемых) значений от теоретически ожидаемых (расчетных). В рассматриваемом примере значение этого показателя составляет 1,930, что является очень хорошим результатом.

8 Predictorr - влияющие переменные (константа): расходы на покупки. b Predictors - влияющие переменные (константа): расходы на покупки,
расходы на проживание. с nredictors - влияющие переменные (константа): расходы на покупки,
расходы на проживание, расходы на питание. d Dependent Variable - зависимая переменная: общие расходы на отдых.
В последнем столбце таблицы «ANOVA» (см. табл. 4.5) значение показателя «Статистическая значимость» (S g.) должно быть меньше или равно 0,05. В нашем примере для всех трех моделей этот показатель составляет 0,000. Это свидетельствует о том, что регрессионные модели, построенные на основе данных респондентов, попавших в выборку, справедливы для всей генеральной совокупности в целом.
В табл. 4.6 представлены параметры моделей, построенных в результате линейного регрессионного анализа. В рассматриваемом примере результатом анализа является третья регрессионная модель, включающая все независимые переменные.

Интерпретация результатов таблицы начинается с рассмотрения статистических показателей, характеризующих коллинеарность (наличие взаимосвязи) между независимыми переменными регрессионной модели (Collinearity Statistics). Значение показателя «Tolerance» должно превышать 0,1, а значение показателя «VIF» должно быть менее 10. В рассматриваемом примере значение «Tolerance» составляет 0,907, а «VIF» — 1,102, что свидетельствует о невозможности возникновения нежелательного эффекта муль- ти кол л и неарн ости.
Стандартизированные коэффициенты регрессии (Beta) показывают относительную значимость независимых переменных, включенных в регрессионную модель. Иными словами, они показывают, как сильно влияют исследуемые факторы (независимые переменные) на итоговую величину (зависимую переменную).
В рассматриваемом примере наибольшей значимостью обладает первая независимая переменная (Beta = 0,613). Это означает, что расходы на крупные покупки могут почти в два раза увеличить сумму общих расходов на отдых по сравнению с расходами на проживание (Beta = 0,366) и питание (Beta = 0,313).
Результаты анализа можно объяснить тем, что расходы на питание и проживание в отеле/пансионе во время отдыха являются запланированными. Изменение этих расходов не ведет к резкому изменению расходов на отдых в целом. Что касается расходов на такие крупные покупки, как одежда, обувь, фотоаппаратура, спортивное снаряжение и т.п., то они, как правило, не являются запланированными. Туристы, отправляясь на отдых в курортную зону «Баварский лес», не планируют крупных покупок, поскольку этот регион не отличается низкими ценами. Именно поэтому совершение крупных покупок способно привести к резкому увеличению расходов на отдых.
В табл. 4.6 представлены также нестандартизированные коэффициенты регрессии (В). Они являются наиболее важными показателями результатов анализа, поскольку используются для построения регрессионной модели (регрессионного уравнения).
Следует отметить, что постоянный член рефессионного уравнения (Constant) в данном случае имеет достаточно большую величину (44,286). Это свидетельствует о том, что включенные в уравнение независимые переменные не в полной мере описывают зависимую переменную. В нашем примере это означает, что среди расходов на отпуск кроме затрат на покупки, оплаты проживания и расходов на питание существуют другие важные статьи затрат, например затраты на транспорт.
Результатом линейного регрессионного анализа является модель линейной регрессии (регрессионное уравнение)

где у — общие расходы туристов на проведение отдыха;
х1 — расходы на покупки (одежды, обуви, галантерейных товаров, украшений, фотоаппаратуры и т.д.);
х2 — расходы на проживание в отеле или пансионе (включая
расходы на обслуживание);
х3 — расходы на питание (покупки продуктов в магазинах, посещение кафе и ресторанов).
Регрессионная модель является универсальной, поскольку описывает 87,9% случаев, т.е. ответов респондентов о структуре их расходов на отпуск. Она может быть использована специалистами по маркетингу при решении вопросов ценообразования в исследуемой курортной зоне.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите цели проведения и возможности использования результатов регрессионного анализа.
2. Какие требования предъявляются к переменным, участвующим в проведении регрессионного анализа, в отношении типов шкал измерения?
3. Как выглядит математическое описание регрессионной модели для простой и множественной линейной регрессии?
4. Что характеризуют коэффициент детерминации и коэффициент R-квадрат, рассчитываемые при проведении регрессионного анализа?
5. Как можно интерпретировать результаты, если значение коэффициента детерминации составляет 0,708, а коэффициента R-квадрат — 0,623?
6. С какой целью в ходе проведения регрессионного анализа производится тест Дарбина—Уотсона? Как можно интерпретировать результаты, если значение этого показателя составляет 1,487?
7. С какой целью в ходе проведения регрессионного анализа производится тест «ANOVA»? Как следует интерпретировать результаты, если величина «Significance» («Значимость») по результатам этого теста составляет 0,03?
8. Для чего служат стандартизированные (Beta) и нестандартизирован- ные (В) коэффициенты регрессии?
9. Какие команды SPSS используются для построения диаграммы рассеяния и тренда, иллюстрирующего результаты простой линейной регрессии?
10. В чем заключается особенность представления результатов множественного регрессионного анализа при использовании пошаговых методов включения переменных в регрессионную модель?
11. В чем заключается эффект мультиколлинеарности при проведении множественного регрессионного анализа и по каким показателям определяется возможность возникновения этого эффекта?
ФАКТОРНЫЙ АНАЛИЗ
5.1. ПОСТАНОВКА ЦЕЛИ ИССЛЕДОВАНИЯ И ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ В SPSS
Факторный анализ позволяет разделить массив переменных на малое число групп, которые называются факторами. В один фактор объединяются несколько переменных, имеющих плотную корреляцию между собой и слабую корреляцию с переменными, объединяемыми другими факторами.
Основнс задачей факторного анализа является группировка схожих по смыслу утверждений в макрокатегории (факторы) с целью сократить число переменных и упростить процедуру анализа существующей базы данных.
Факторный анализ, как правило, предшествует другим видам анализа, например кластерному. Для примера рассмотрим факторный анализ с целью сокращения массива данных, содержащего
|
|
|


