Функции групповых центройдов

Structure Matiix* Посещение дискотек Function   Да Нет -1,104 ,104

* Нестандартизированные канонические дискриминантные функции, которые оцениваются по групповым средним значениям.

 

Как видно из данных, представленных в табл. 7.11, средние значение дискриминантной функции для группы туристов, посещающих дискотеки, составляет -1,104, а среднее значение дискриминантной функции для группы туристов, не посещающих дискотеки, составляет 0,104. Чем больше расстояние между средними значениями дискриминантной функции в исследуемых

147

группах, тем более четко прослеживается различие между исследуемыми группами.

Четкость различия между исследуемыми группами зависит также от рассеяния значений дискриминантной функции в исследуемых группах. Это рассеяние показано на графиках распределения значений дискриминантной функции в исследуемых группах (рис. 7.9 и 7.10).

 

 

 

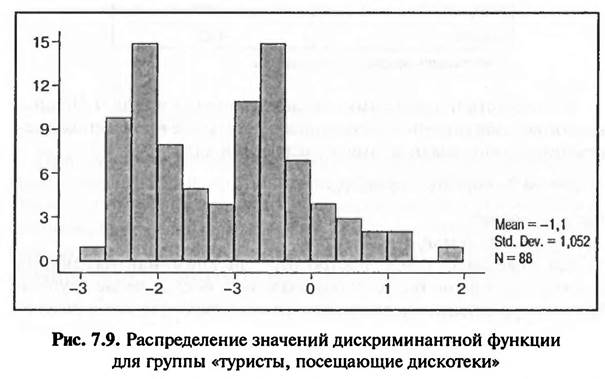
Чем больше рассеяние значений дискриминантной функции в исследуемых группах, тем шире область их пересечения и слабее четкость различия между исследуемыми группами. Следовательно, чем больше такое рассеяние, тем сложнее однозначно определить принадлежность респондента к одной из исследуемых трупп.

На основе построенной нами дискриминантной модели, можно сделать прогнозы посещения дискотек определенным туристом исходя из его возраста и уровня дохода семьи. Например, для туриста в возрасте 20 лет, принадлежащего по уровню дохода семьи к категории «7» (2800 — 3300 евро), значение дискриминантной функции составит

Согласно данным, представленным на рис. 7.9, в исследуемую группу «туристы, посещающие дискотеки» входят 88 туристов. Значение дискриминантной функции близкое к -2,246 имеют 15 человек.

Поданным, представленным на рис. 7.10, исследуемая группа «туристы, не посещающие дискотеки» включает 935 человек. Значение дискриминантной функции, близкое к -2,246, имеют примерно 10 человек. На основании вышеизложенного можно сделать вывод, что турист в возрасте 20 лет, принадлежащий по уровню дохода семьи к категории «7» (2800—3300 евро), скорее всего, будет посещать дискотеки.

7.5. ОПРЕДЕЛЕНИЕ ТОЧНОСТИ ПРОГНОЗОВ НА ОСНОВЕ ПОСТРОЕНHOЙ ДИСКРИМИНАНТНОЙ МОДЕЛИ

Точность прогнозов на основе построенной дискриминантной модели оценивается по результатам классификации, т.е. распределения объектов исследования (туристов) по исследуемым группам (посещающие и не посещающие дискотеки).

В табл. 7.12 представлены результаты классификации отдельно по каждому наблюдению, т.е. по каждому респонденту, принявшему участие в опросе и предоставившему информацию о своем возрасте и доходе семьи. Поскольку число респондентов слишком велико, в табл. 7.12 представлены только 20 наблюдений, первых по списку, — как было указано при формировании задания на проведение дискриминантного анализа (см. рис. 7.8).

В столбце «Actual Group» (см. табл. 7.12) указывается фактическая принадлежность респондента к одной из исследуемых групп. Так, первый по списку респондент не посещает дискотеки («2»). Остальные респонденты не ответили на вопрос, посещают ли они дискотеки, поэтому в столбце «Actual Group» стоит отметка «ип- grouped» («Несгруппированное наблюдение»). Такое большое число несгруппированных наблюдений не должно удивлять. Из 6396 респондентов, принявших участие в опросе, 4717 туристов, указав свой возраст и доход семьи, не дали информации о том, посещают ли они дискотеки.

 

В столбце «Predicted Group» указывается прогнозируемая принадлежность респондента к одной из исследуемых групп, определяемая на основе построенной дискриминантной модели. Если прогнозируемая принадлежность к группе не совпадает с фактической, ее значение отмечается двумя звездочками (**).

В столбце «Р (G = g\D = d)» табл. 7.12 указывается вероятность, с которой конкретный респондент может быть причислен к прогнозируемой группе. В столбце «Discriminant Scores» указывается значение дискриминантной функции.

Например, значение дискриминантной функции для первого респондента составляет -3,327. Согласно построенной дискриминантной модели этот респондент с вероятностью 97,2% может быть причислен к группе туристов, посещающих дискотеки, в действительности же он не посещает дискотеки.

К сожалению, из-за большого числа несгруппированных наблюдений табл. 7.12 не показывает, сколько представленных результатов классификации из 20 являются ошибочными. В результате по данным этой таблицы нельзя составить даже приблизительного представления о точности прогнозов на основе построенной дискриминантной модели.

Точность прогнозов на основе построенной дискриминантной модели определяется из данных сводной таблицы результатов классификации, т.е. причисления объектов исследования к одной из исследуемых групп (табл. 7.13).

 

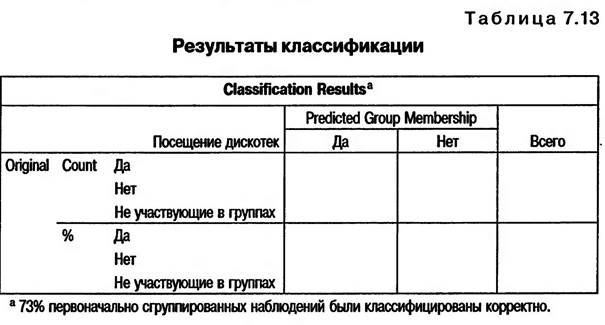
Из данных табл. 7.13 «Результаты классификации» видно, что исследуемая группа туристов, посещающих дискотеки, состоит фактически из 88 человек. Согласно построенной дискриминантной модели 62 туриста из 88 были корректно причислены к этой группе, а 26 — по ошибке причислены к группе туристов, не посещающих дискотеки. Итак, корректные результаты классификации составили 70,5%, а ошибочные — 29,5%.

По данным этой же таблицы исследуемая группа туристов, не посещающих дискотеки, состоит фактически их 935 человек. Согласно построенной дискриминантной модели 686 туристов из 935 были корректно причислены к этой группе, а 249 — по ошибке причислены к группе туристов, посещающих дискотеки. Итого корректные результаты классификации составили 73,4%, а ошибочные — 26,6%.

В иелом корректные результаты классификации составили 73,1%, т.е. в 73,1% случаев фактическая принадлежность!уриста к группе посещающих или не посещающих дискотеки совпадает с прогнозируемой, определенной на основе построенной дискриминантной модели. Это дает возможность сделать вывод, что точность прогнозов, сделанных на основе построенной дискриминантной модели составляет примерно 73%.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назовите цель проведения и возможности использования результатов дискриминантного анализа.

2. Как выглядит математическое описание дискриминантной модели?

3. Какие требования предъявляются к переменным, участвующим в дискриминантном анализе, относительно типов шкал измерения переменных?

4. Какие задачи решаются в ходе проведения дискриминантного анализа?

5. Каким образом и с какой целью выявляется наличие дискриминирующих свойств у переменных, выбранных в качестве независимых (дискриминационных) переменных дискриминантной модели?

6. Как можно интерпретировать результаты теста на равенство средних величин в группах, проводимого в ходе процедуры дискриминантного анализа, если значение «Significance» («Значимость») для определенной дискриминационной переменной составляет 0,637?

7. Что характеризует и с какой целью рассчитывается коэффициент корреляции между дискриминационными переменными? Как можно интерпретировать результаты таких расчетов, если значение коэффициента корреляции между двумя дискриминирующими переменными составляет 0,52?

8. Что характеризует и для чего рассчитывается коэффициент корреляции между расчетными значениями дискриминантной функции и реальной принадлежностью респондента к определенной группе? Как можно интерпретировать результаты, если значение этого коэффициента составляет 0,485?

9. Для чего в ходе проведения дискриминантного анализа рассчитывается показатель Лямбда Уилкса, как следует интерпретировать результаты, если значение величины «Significance» («Значимость») при расчете этого показателя составляет 0,02?

10. Для чего служат стандартизированные и нестандартизированные коэффициенты дискриминантной функции? Как следует интерпретировать результаты, если значения стандартизированных коэффициентов составляют: для дискриминационной переменной «1» — 0,692; дпя дискриминационной переменной «2» — 0,346?

11.Что характеризует расстояние между средними значениями и распределение дискриминантной функции в исследуемых группах?

12.Что представляет собой сводная таблица результатов классификации, выводимая в SPSS на экран компьютера среди результатов дискриминантного анализа, какие выводы можно сделать на основе данных этой таблицы?

ЗАКЛЮЧЕНИЕ

В странах с развитой рыночной экономикой, в частности в Германии, где темпы роста рынков отдельных товаров и услуг незначительны или рост вообще отсутствует, конкурирующие фирмы работают в условиях жесткой борьбы за потребителя. Для достижения успеха в этой борьбе активно используется весь спектр современных технологий маркетинговых исследований, в том числе предполагающих обработку информации при помощи статистических методов анализа.

Современные маркетологи должны владеть знаниями в области статистического анализа и навыками работы с соответствующими программными продуктами, наиболее популярным из которых в Европе является программа SPSS.

В Германии такие знания являются обязательными для студентов, обучающихся по специальности «Маркетинг». Все дипломные проекты и диссертационные исследования, которые защищаются по этой специальности, как правило, предполагают анализ информации с использованием программного пакета SPSS.

Пособие предназначено для российских студентов, обучающихся по специальности «Маркетинг», а также для всех желающих самостоятельно освоить основы статистического анализа в маркетинговых исследованиях.

Данная работа представляет лишь небольшую часть возможностей, предоставляемых пользователям SPSS. В частности, были рассмотрены не все методы статистического анализа, часто применяемые на практике, такие, как, например, многофакторный и многомерный дисперсионный анализ, логистическая регрессия и др. Для ознакомления с этим материалом рекомендуется использовать источники, указанные в списке литературы.

СПИСОК ЛИТЕРАТУРЫ

1. Бююль Ахам, Цефель Петер. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей: Пер. с нем. СПб.: ДиаСофтЮП, 2002.

2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. 9-е изд. М.: Высшая школа, 2003.

3. Плис А.И., Слиеина Н.А. Практикум по прикладной статистике в среде SPSS: Учеб. пособие. В 2-х ч. Ч. 1. Классические процедуры статистики. М.: Финансы и статистика, 2004.

4. Таганов Д. Н. SPSS: Статистический анализ в маркетинговых исследованиях. СПб.: Питер, 2005.

5. Янкевич B.C., Безрукова Н.Л. Маркетинг в гостиничной индустрии и туризме: российский и международный опьгг/ Под ред. B.C. Янкевича. М.: Финансы и статистика, 2003.

6. Backhaus Klaus, Erichson Bemd, P/inke Wulff, Weiber Rolf. Multivariate analysemethoden. E ne anwendungsor entierte Einfu'irung. 9 Auflage. Berlin: Springer, 2000.

7. Brosius Felix, SPSS 11. Fundierte Einfuhrung in SPSS und Stati;t.k. Bonn: mitp-Verlag, 2002.

8. BiihlAchim, Zdfel Peter. SPSS 11. Einfuhrung in die moderne Datenanalyse unter Windows. Munchen: Pearson Studium, 2002.

9. Jassen Jiirgen, Laatz Wilfried. Statistische Datenanalyse mit SPSS fur Windows. Eine anwendungsorientierte E nfuhrung in das Basissystem und das Modul exakte Tests. Berlin: Springer, 2003.

10. Schmalen Helmut. Grundlagen und Probleme der Betribswirtschaf. 12 Auflage. Stuttgard: Schaffer- Poeschel Verlag, 2002.

11. Wittenberg Reinhard. Datenanalyse mit SPSS fur Windows. Stuttgart: Lucius& Lucius, 2003.

Оглавление

введение..................................................... 3

1. Основы статистического анализа

в маркетинговых исследованиях............... 4

1.1. формирование статистической выборки................ 4

1.2. основные методы статистического анализа........... 9

1.2.1. Кластерный анализ...................................................... 9

1.2.2. Дискриминантный анализ_______________________________ 11

1.2.3. Регрессионный анализ___________________________________ 13

1.2.4. Факторный анализ....................................................... 15

1.2.5. Дисперсионный анализ................................................. 17

2. Формирование исходной базы данных

в spss.................................................... 21

2.1. структура редактора данных................................... 21

2.2. виды кодировки........................................................ 29

2.3. типы шкал измерения переменных..................... 35

3. сравнение средних величин в spss............ 42

3.1. Т-тест для независимых выборок.......................... 44

3.1.1. Постановка цели исследования и представление

Исходных данных в spss...................................... 44

3.1.2. Команды spss на выполнение т-теста

Для независимых выборок............................................ 47

3.1.3. Интерпретация результатов г-теста

Для независимых выборок............................................ 4?

3.2. Однофакторный дисперсионный анализ.............. 51

3.2.1. постановка цели исследования и представление исходных данных в spss................................................... 51

3.2.2. команды spss на выполнение однофакторного дисперсионного анализа................................................................... 54

3.2.3. Интерпретация результатов однофакторного дисперсионного анализа................................................................... 58

4. Линейный регрессионный анализ в spss.... 65

4.1. простая линейная регрессия................................. 67

4.1.1. постановка цели исследования и представление исходных данных в spss............................................................ 67

4.1.2. команды spss на выполнение простого регрессионного анализа 70

4.1.3. интерпретация результатов простого регрессионного анализа 73

4.1.4. Графическое представление простой регрессионной модели в spss........................................................................ 75

4.2. множественная линейная регрессия................... 79

4.2.1. постановка цели исследования и представление исходных данных в spss........................................................... 79

4.2.2. Команды spss на выполнение множественного регрессионного анализа................................................................... 81

4.2.3. Интерпретация результатов множественного регрессионного анализа................................................................... 83

5. факторный анализ................................. 89

5.1. Постановка цели исследования

И представление исходных данных в spss........ 89

5.2. Команды spss на выполнение факторного

Анализа...................................................................... 94

5.3. Оценка пригодности исходных данных

Для выполнения факторного анализа.................. 99

5.4. выявление корреляционной зависимости между переменными исходного массива.................... 100

5.5. определение оптимального числа компонентов факторной модели................................................ 103

5.6. Построение факторной модели

И интерпретация результатов.............................. 105

5.7. Сохранение компонентов факторной модели в качестве новых переменных

Базы данных........................................................... 109

6. иерархический кластерный анализ......... 112

6.1. Постановка цели исследования

И представление исходных данных в spss...... 112

6.2. команды spss на выполнение иерархического кластерного анализа........................................... 116

6.3. сравнение объектов исследования................... 121

6.4. порядок формирования кластеров.................... 124

6.5. Определение оптимального количества формируемых кластеров..................................... 126

6.6. Интерпретация результатов кластерного анализа 127

7. дискриминантный анализ...................... 131

7.1. Постановка цели исследования

И представление исходных данных в spss...... 131

7.2. Команды spss на выполнение дискриминантного анализа................................................................... 134

7.3. оценка выбора дискриминационных переменных.................................................................................. 139

7.4. построение дискриминантной модели............... 145

7.5. Определение точности прогнозов

На основе построенно 1 дискриминантной модели................................................................................... 149

заключение............................................... 154

список литературы.................................... 155

По вопросам приобретения книг обращайтесь:

Отдел продаж «ИНФРА-М» (оптовая продажа):

127282, Москва, ул. Полярная, д. 31 в, тел.: (495) 380-4260; факс: (495) 363-9212

E-mail: books@infra-m.ru •

Магазин «Библиосфера» (розничная продажа):

109147, Москва, ул. Марксистская, д. 9, тел. (495) 670-5218, 670-5219

Отдел «Книга—почтой»:

тел. (495) 363-4260 Сдоб. 232, 246)

Центр комплектования библиотек: 119019, Москва, ул. Моховая, д. 16 (Российская государственная библиотека, кор. К)

тел. (495) 202-9315

Учебное издание

Гертруда Моосмюллер,

Наталья Николаевна Ребик

МАРКЕТИНГОВЫЕ ИССЛЕДОВАНИЯ

С SPSS

УЧЕБНОЕ ПОСОБИЕ

Редактор JI. Е. Миронова Корректор Л. С. Куликова Компьютерная верстка О.В. Савостиной

Подписано в печать 23.06.2006. Формат 60x88/16. Бумага офсетная. Гарнитура Newton. Печать офсетная. Усл. печ. л. 9,8. Уч.-изд. л. 9,51. Доп. тираж 1500 экз. Заказ № 9484.

Издательский Дом «ИНФРА-М» 127282, Москва, ул. Полярная, д. 31 в. Тел.: (495) 380-05-40, 380-05-43. Факс: (495) 363-92-12.

E-mail: books@infra-m.ru http://www.infra-m.ru

Отпечатано с готовых диапозитивов в ОАО ордена «Знак Почета» «Смоленская областная типография им. В. И. Смирнова». 214000, г. Смоленск, проспект им. Ю. Гагарина, 2

^[1] Тест Ливина (Levene's Test) — тест на равенсгво дисперсий в исследуемых группах. Дисперсия характеризует рассеяние значений переменной вокруг ее среднего значения. При сравнении средних величин в исследуемых группах необходимо принимать во внимание равенство или неравенство дисперсий.

Тест Ливина проверяет исходную (нулевую) гипотезу: «Дисперсии в исследуемых группах равны». Результат теста Ливина определяется значением показателя Significance («Значимость»). Если значение Significance не превышает 0,05, это означает, что вероятность ошибки при отклонении нулевой гипотезы составляет менее 5% (т.е. ниже допустимого уровня при доверительном интервале 95%). В этом случае исходная гипотеза может быть отклонена, т.е. она неверна. Значение Significance менее 0,05 доказы­вает ошибочность исходной гипотезы и статистическую значимость раз­личия дисперсий в исследуемых группах.

^[2] Лямбда Уилкса (Wilks' Lambda) — это критерий, используемый при прове­дении теста на предмет того, значимо ли различаются между собой сред­ние значения дискриминантной функции в исследуемых группах.

Построенная дискриминантная модель (дискриминантная функция) должна отражать четкое разделение исследуемых групп. Для оценки чет­кости этого разделения проводится тест с помощью критерия Лямбда Уилкса. В качестве исходной гипотезы выступает утверждение: «Средние значения дискриминантной функции в исследуемых группах равны». Верность исходной гипотезы определяется значением показателя «Significance». Если значение «Significance» не превышает 0,05, это означает, что вероятность ошибки при отклонении нулевой гипотезы состав­ляет менее 5% (т.е. ниже допустимого уровня при доверительном интер­вале 95%). В этом случае исходная гипотеза может быть отклонена, т.е. она неверна. Значение «Significance» менее 0,05 доказывает ошибочность ис­ходной гипотезы и статистическую значимость различия средних значе­ний дискриминантной функции в исследуемых группах.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: