 |
Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС.
|
|
|
|
Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике.
Метод позволяет отыскать условные или относительные экстремумы функции, которые являются ее минимумом или максимумом при выполнении дополнительных условий в форме равенств, т.е. уравнений связи.
Данный метод дает возможность найти систему уравнений, которой удовлетворял экстремум функции 
на множестве N. Для того чтобы найти экстремум, характеризующийся на множестве N вектором 
необходимо найти m чисел 
, которые совместно с вектором 
удовлетворяют 
уравнениям с 
неизвестными.
Эти уравнения получены как условный экстремум функции Лагранжа.
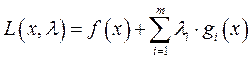
Структура энергосистемы
(РФ,1996)
Цена (АЭС) > Цена (КЭС) > Цена (ГЭС)
tпуск=часы tпуск=1 мин
ТЭС – тепловая система;
ТЭС+ГЭС – гидротепловая (смешанная) система.
Параметры энергосистемы:
- технологические:
а) ГЭС (расход пара, напор);
б) ТЭС (расход пара, расход охлаждающей воды);
- электромеханические (
).
Тепловая и гидротепловая системы. Структура энергосистемы и декомпозиция задачи наивыгоднейшего распределения нагрузки в энергосистеме. Иерархия данной задачи в пространстве, времени и ситуации.
Руст- установившееся активная мощность.
Руст=РГЭС+РГАЭС+РКЭС+РТЭЦ+РГТУ+РПГУ+РАЭС+Рпр.
Р*=Рi / РУСТ.
Так Р*ГЭС=0,14; Р*КЭС=0,46; Р*ТЭЦ=0,24; Р*АЭС=0,16.
Цена (АЭС)> Цена (КЭС)> Цена (ТЭС).
Тепловая система: ТЭС.
А если ТЭС+ГЭС, то получиться гидротепловая система.
Параметры: 1-технологические;
2-электротехнические.
Технологические деляться на:
-Расходы напора на ГЭС;
-Расходы пара на ТЭС.
Электротехнические: Uy, IB, P, Q, KTP.
Одной из главных задач управления ЭС в условиях нормальной эксплуатации является задача наивыгоднейшего распределения нагрузки между генераторами, что обеспечивает высокую эффективность использования трудовых, материальных и экономических ресурсов.
|
|
|
Данная задача имеет декомпозицию (разделение) в пространстве, времени и ситуации.
А). Уровни в разделение по пространству:
1.Распределение нагрузки между ОЭС и ЕЭС;
2.Распределение нагрузки между РЭС и ОЭС;
3.Распределение нагрузки между ЭС и РЭС;
4.Распределение нагрузки между агрегатами ЭС.
Б). Разделение по времени:
1.Долгосрочное планирование (мес.,год)- определение прогнозируемых графиков нагрузки, необходимых для проведения технологических и хозяйственных мероприятий.
2.Краткосрочное планирование (мес.,сут.)- определение плановой нагрузки ЭС.
3.Регулирование мощности в ЭС в темпе производств, протекающих в ЭЭС.
В). Разделение по ситуации:
1.Нормальный режим.
2.Аварийный режим.
3.Послеаварийный режим.
Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС.
Пусть имеется ЭС с числом n ТЭС, для которых заданы расходные характеристики Bi (Pi) (на i-ой ТЭС) суммарная нагрузка РS.
Задачу навыгоднейшего распределения нагрузки рассмотрим при помощи метода Лагранжа:
1) Уравнение цели: 
где В- суммарный расход топлива.
2) Уравнение связи: 
3) Уравнение ограничений: 
где РS-суммарная нагрузка.
П- потери.
4) Функция Лагранжа: 
.
Дифференцируя функцию Лагранжа по РГ1….PГn и приравняв все производные к нулю, получим:
………….…………………………………………………
………….………………………………………………….
Таким образом, условия оптимизации:
---относительный прирост расхода топлива (на сколько изменится расход топлива, если мощность i-ой станции измениться на ¶Рi).
---относительный прирост потерь активной мощности (на сколько изменяться потери активной мощности, если мощность i-ой станции измениться на ¶Рi)
|
|
|
Условие оптимальности распределения нагрузки:
Если 
и выполняется условие оптимальности, то функции соответствует min, иначе max.
Физический смысл условия оптимальности:
--мощность доведенная до потребителя.
Если 
, то на какой либо эл. станции наблюдается чрезмерный расход топлива, т.е. не рациональное распределение нагрузки, не экономично.
Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Структурная схема алгоритма.
Пусть имеется ЭС с числом n ТЭС, для которых заданы расходные характеристики Bi (Pi) (на i-ой ТЭС) суммарная нагрузка РS.
Задачу навыгоднейшего распределения нагрузки рассмотрим при помощи метода Лагранжа:
5) Уравнение цели: 
где В- суммарный расход топлива.
6) Уравнение связи: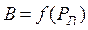 
7) Уравнение ограничений: 
где РS-суммарная нагрузка.
П- потери.
8) Функция Лагранжа: 
.
Дифференцируя функцию Лагранжа по РГ1….PГn и приравняв все производные к нулю, получим:
………….…………………………………………………
………….………………………………………………….
Таким образом, условия оптимизации:
---относительный прирост расхода топлива (на сколько измениться расход топлива, если мощность i-ой станции измениться на ¶Рi).
---относительный прирост потерь активной мощности (на сколько изменяться потери активной мощности, если мощность i-ой станции измениться на ¶Рi)
Условие оптимальности распределения нагрузки:
Если и выполняется условие оптимальности, то функции соответствует min, иначе max.
Физический смысл условия оптимальности:
--мощность доведенная до потребителя.
Если , то на какой либо эл. станции наблюдается чрезмерный расход топлива, т.е. не рациональное распределение нагрузки, не экономично.
Алгоритм
Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь активной мощности. Физический смысл равенства относительных приростов.
Это случай задачи наивыгоднейшего распределения нагрузки между агрегатами электростанций или в ЭС с высокой концентрацией мощности.
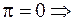
-усл-ие оптимальности, т.е. оно соотв-ет рав-ву отн-ых приростов
Рассмотрим на примере из 2-х агрегатов Эл/ст
|
|
|
Если у двух агрегатов имещих мощн-ь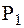 
и 
и возрастные хар-ки 
и отн-ные приросты, не равные друг другу (
).
Догрузим агрегат 1 на некоторое значение 
, а агрегат 2 –разгрузим наэто же
Когда 
, дальнейшее перераспределение нагрузки не принесёт экономии 
мы имеет наив-шее распр- ие нагр-и – оптим. режим.
Алгоримт оптим-ции с испол-ем ЭВМ.
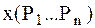- берётся произ-ое распт- ие нагр-ки м/у эл/ст
|
|
|
