 |
Учет ограничений в форме неравенств
|
|
|
|
При оптимизации режима энергосистемы может быть задана совокупность ограничений.
Ограничения в форме неравенств (область допустимых режимов)
-ограничение по мощности
- ограничение по стоку ГЭС. 
Если мы нашли граничную точку и в дальнейшем будем рассматривать ограничение как равенство, то в результате будет найден экстремум Х``, принадлежащий также линии ограничения Х``≠Х*.
Для решения задачи отыскания экстремума целевой функции F(x,y) в допустимых областях DY, DZ рассматривается новая функция
W=F(x,y)+Ш(y)+Ш(z) – целевая функция + штрафная функция
Если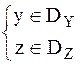 
, то Ш=0 Ш(y)=0, Ш(z)=0 
Если зависимая переменная (y и z) соответствующей точки XK удовлетворяет неравенству yMIN≤y≤yMAX, zMIN≤z≤zMAX, т.е. yєD, zєD, то в таком случае Ш(у)=Ш(z)=0 → W=F(x), в противном случае накладывается штраф в виде положительной надбавки к целевой функции. Чем существеннее становится отклонение от допустимого режима, тем больше становится штраф. Штраф не должен соответствовать реальному ущербу, наносимому ограничениями. Возрастание штрафной функции при нарушении ограничений должно происходить быстрее, чем убывание целевой функции благодаря нарушению ограничений.
W=F+Ш → нарушается критерий оптимальности итерационного процесса 
.
При надлежащем выборе функции Ш при учете критерия оптимальности движение всегда будет осуществляться в сторону допустимой области
Требования к целевой функции:
1) W*=F* - исходная целевая функция
2) При нарушении ограничений Ш возрастает быстрее, чем убывает F
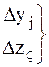степень ЗП за пределом D (степень нарушения ограничения)
величины, приводящие размер-ть функции штрафа к размерности целевой функции
F(x,y)- в тоннах условного топлива (ТУТ) δU – кВ; СU=ТУТ/кВ2
|
|
|
-хуже сходимость; 
- лучше сходимость, но возможно несовпадение минимумов F*=W*
24 Оптимизация режима ЭЭС методом Ньютона. Матрица Гессе. Геометрическая интерпретация аппроксимации целевой функции
Внедерение ЭВМ позволило использовать более современные методы решения задач на экстремум, такие, как обобщенный метод Ньютона. Данный метод характеризуется малым (не более 10) количеством шагов итерации.
Сущность метода: Искомая целевая функция замещается в точке начального приближения полиномом второй степени, т.е. параболой, а затем отыскивается его экстремум.
В точке Х(0) аппроксимируем
Точка экстремума: 
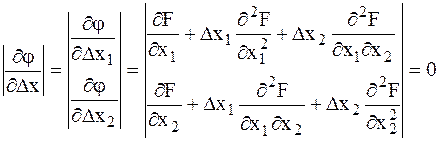
- матрица Гессе 2-го порядка
Истинная сложная зависимость целевой функции от параметров Х1, Х2 в точке Х(0) заменяется параболоидом, который в проекции Х1, Х2 – эллипс. Центр этого эллипса соответствует минимуму оптимизирующей функции.
При отыскании минимума целевой функции полезна замена целевой функции полиномом именно второго порядка, так как расходные характеристики ТЭС (В(р)) неплохо аппроксимируется кривыми именно второго порядка.
, G- матрица Гессе
1.Понятие оптимизации. Основные задачи оптимизации в электроэнергетике
2.Применение метода множителей Лагранжа при решении задач оптимизации.
3.Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС.
4.Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь активной мощности. Физический смысл равенства относительных приростов.
5.Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относительные приросты ТЭС и ГЭС.
6.Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме.
7.Оптимальное распределение нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения.
|
|
|
8.Оптимальное распределение нагрузки при переменном напоре ГЭС.
9.Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения агрегатов электростанций.
10. Оптимизация режима с учетом потерь активной мощности при передаче. Метод линейных коэффициентов токораспределения.
11.Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения: линия поверхности равного уровня целевой функции, допустимая и результирующая области,
12.Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике. Возможные направления. Градиент и антиградиент целевой функции. Способы задания длинны шага. Метод оптимизации при постоянной длине шага.
13.Применение метода наискорейшего спуска при решении задач оптимизации в электроэнергетике.
14.Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике.
15.Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода.
16.Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод в сочетании с методом наискорейшего спуска.
17.Применение градиентных методов оптимизации в электроэнергетике. Метод проецирования градиента.
18.Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент.
19.Учет ограничений в форме неравенств при решении задач оптимизации в электроэнергетике.
20. Применение метода штрафных функций при решении задач оптимизации в электроэнергетике.
21.Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе. Геометрическая интерпретация аппроксимации целевой функции. Обобщенный метод Ньютона.
22. Комплексная оптимизация режимов энергосистемы.
23. Применение метода приведенного градиента для оптимизации режима электрической сети. Оптимизация модулей и фаз узловых напряжений при наличии ИРМ в нагрузочных узлах.
|
|
|
24. Применение метода приведенного градиента для оптимизации режима электрической сети. Оптимизация коэффициента трансформации в центре питания распределительной сети.
|
|
|
