 |
Оптимальное распределение нагрузки между агрегатами эл/ст.
|
|
|
|
Использование метода множителей Лагранжа позволяет получить условие наивыгоднейшего распределения нагрузки между агрегатами эл/ст. в виде равенств отношений приростов расхода первичного ресурса (приведенной мощности) к приращению вторичного ресурса (полезной мощности) при соблюдении балансовых ограничений.
1)М/у агрегатами ТЭС:
а) м/у турбинами
б) м/у котлами
в) м/у блоками
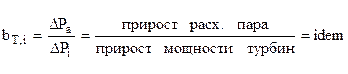bT,I – относительный прирост турбины
bk,I - относительный прирост котлов
bБ,I – относительный прирост блока блок=котел+турбина
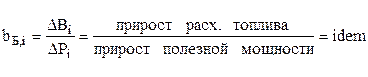
bT,I = idem (i)
На эти уравнения накладываются ограничения, т.к. характеристики имеют скачки и участки постоянного прироста.
dT dT
P1 Р1>P2 P2
Pmin1турб.1 Pmax1 Pmin2турб.2 Pmax2
Pmin=Pmin1+Pmin2
1. Pmin<P<Pmin+P2 – загрузка агр.2
2. Pmin+P2<P<P1+P2 – загрузка агр.2
3. P1+P2<P<P1+Pmax2 – загрузка агр.2
4. P>P1+Pmax2 – загрузка агр.1
При такой методике всегда используется агрегат с наибольшей экономией топлива. Если агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания их относительных приростов.
2) Распределение нагрузки м/у агрегатами ГЭС
Распределение нагрузки м/у агрегатами ГЭС является наивыгоднейшим, если они работают с одинаковыми относительными приростами.
Задача наивыгоднейшего распределения нагрузки м/у агрегатами станций проста, если известны характеристики относительных приростов. Но в условиях эксплуатации желательно использовать не характеристики, а измерение относительных приростов.
Для этого с малым шагом дискретности измеряем а1 и а2 и соответствующие им Р1 и Р2.
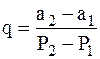
14.Формул-ка з-чи опт-ции режима ЭС с позиции нелин-го прогр-ия. Осн-ные опред-ния. Линия пов-сти равного уровня ЦФ, доп-мая и рез-щая обл-ти, абс и усл экстр-м ЦФ, акт и пасс огран-ния. Выр-е ЦФ ч/з завис и независ переменные, Ур-ния связи.
|
|
|
Общая задача нелинейного программирования заключается в отыскание экстремума целевой функции при задании ограничения в виде равенств и неравенств.
Целевая функция суммарный расход топлива в ЭС.
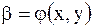-функция от независимых и зависимых переменных.
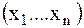
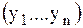-вектор независимых и зависимых переменных.
- 
, 
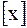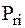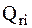, i=1…..n-мощности станции ЭС.
- 
, 
, 
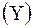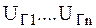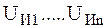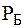-напряжение генераторных и нагр-ых узлов и мощность балансирующего узла
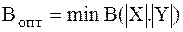с учетом связи 
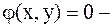м/у зависимых переменных.
В качестве уравнений связи можем использовать уравнения узловых напряжений
УС=УУН
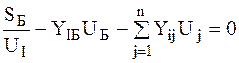
матричный вид
в-р полных мощностей 
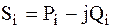
Выразим целевую Функцию только ч/з независимых переменных
для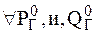 
можно найти 
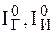исходя из уравнения
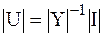
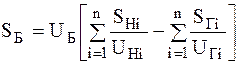
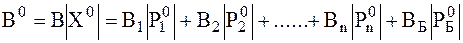
Оптимальный режим должен удовлетворять режимным ограничениям, запишем в общем случае в виде неравенств.
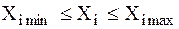
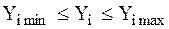
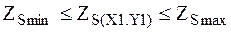
Поверхность равных уравнений целевой функции ─геометрическое место точек в пространстве независимых переменных, в которых целевая функция имеет одно и тоже значение.
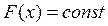
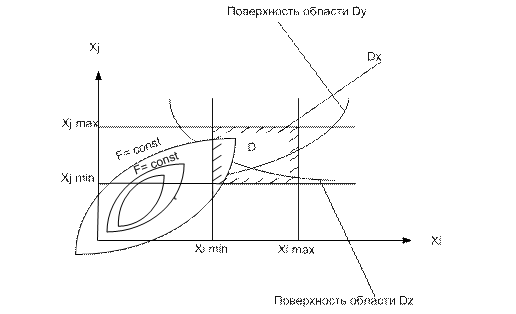Dx – допустимая область по параметрам х. В общем случае, при наличии n-переменных ─ это n – мерный параллелограмм.
Результирующая область
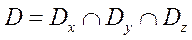Область D называется выпуклой, если для любой пары точек,принадлежащих области,прямая соединяющая эти две точки,также целиком принадлежат области D.
Абсолютный экстремум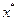 
─ экстремум F (x).
Условный или относительный экстремум─это точка на границе области D, в которой целевая функция имеет не меньшее значение внутри данной области.
, F(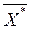
) ─оптимальное решение задачи.
Если целевая функция мультимодальна,то найденное оптимальное решение может быть не глобальным а локальным.В случае унимодальности целевой функции ─ оптимальное решение глобально.
Ограничения 
активные ← z пассивные
Активные ограничения ─в точке условного экстремума ограничения принимают граничные значения.
|
|
|
Вопрос 15.
При анализе ОЭС и ЕЭС возникает необходимость поиска экстр. нелинейной функции на множестве точек, удовлетворяющих нелинейным неравенствам.
Отсюда возникла теория экстремума в нелинейных задачах с ограничениями. Необходимое и достаточное условие существования такого экстремума было сформулировано Куном и Такером.
Теорема Куна-Такера
Если Ц(х)- целевая функция, g(х)- огр-я в форме неравенств, то для того, чтобы точка х была опт-й, т.е. Ц(х0)=min Ц(х) необходимо и достаточно, чтобы существовала точка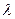 
, которую совместно с х 
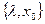, образовало бы седло функции Лагранжа.
Функция Лагранжа:
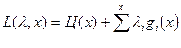
т.е. чтобы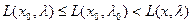 
. Если L(х) и Ц(х) дифференциальные функции, то седловая точка может быть найдена из следующих условий:
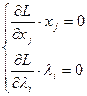
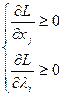
Если ограничения записаны в форме равенств, в таком случае условия Кауна-Такера сводятся к применению метода множ-й Лагранжа
16 Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике. Возможные направления. Градиент и антиградиент целевой функции. Способы задания длинны шага. Метод оптимизации при постоянной длине шага.
|
|
|
